 |
Проекция треугольника, параллелограмма и трапеции.
|
|
|
|
Треугольник изображается треугольником любой формы. Медиана треугольника будет изображаться медианой, так как отношение отрезков сохраняется. При проекции биссектрисы и высоты пойдет искажение.
Так как параллельность прямых сохраняется, то изображение параллелограмма, в частности, прямоугольника, ромба, квадрата, служит параллелограмм. Длина сторон и величины углов произвольные.
Любая трапеция изображается в виде произвольной трапеции. Сохраняется только отношение оснований. Равнобокая трапеция имеет ось симметрии. Ее изображают следующим образом (рис. 10). Каждое из оснований делим пополам и проводим ось симметрии.
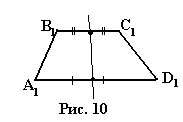
2.4. Проекции правильного шестиугольника.
При построении оригинала правильного шестиугольника используют два симметричных ромба: OBCD и OAFE (рис. 11, а). Изображение же получается при построении ромбов в виде двух одинаковых произвольных параллелограммов. Для получения проекции правильного шестиугольника надо оставшиеся точки соединить (рис. 11, б).
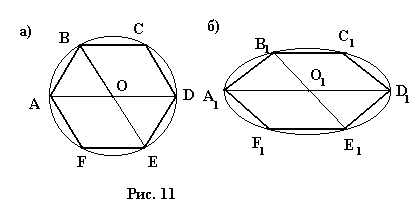
2.5. Проекции тетраэдра и параллепипеда.
Тетраэдр (треугольная пирамида) изображается в виде произвольного четырехугольника с его диагоналями (рис.12, а).
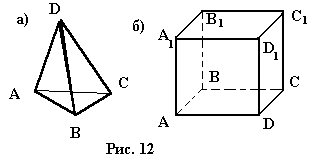 |
Для построения проекции параллепипеда сначала из произвольной точки проводим три луча различной длины, не совпадающие. Затем на каждой паре лучей строим параллелограмм. Полученный каркас достраиваем до параллепипеда (рис. 12,б).
Глава III. Задачи на метрические построения.
Выносные чертежи.
Чертеж, на котором построена фигура Ф0, имеющая форму оригинала заданной плоской фигуры (т. е. подобная фигуре Ф), называют выносным чертежом фигуры Ф.
Если точки P, Q и R принадлежат секущей плоскости и не лежат на одной прямой, а их проекции на плоскость, выбранную в качестве основной, - точки P’, Q’ и R’, то точки пересечения соответственных прямых, т.е. точки S1=PQ∩P’Q’, S2=PR∩P’R’, S3=RQ∩R’Q’, лежат на одной прямой. Эта прямая является основным следом секущей плоскости.
|
|
|
Построение выносных чертежей может быть выполнено вычислительным, а также геометрическим способом.
Задача 1. На ребрах ВВ1 и CD куба ABCDA1B1C1D1 взяты соответственно точки P и Q – середины этих ребер. Построить фигуру, подобную многоугольнику, полученному в сечении кубу плоскостью С1PQ.
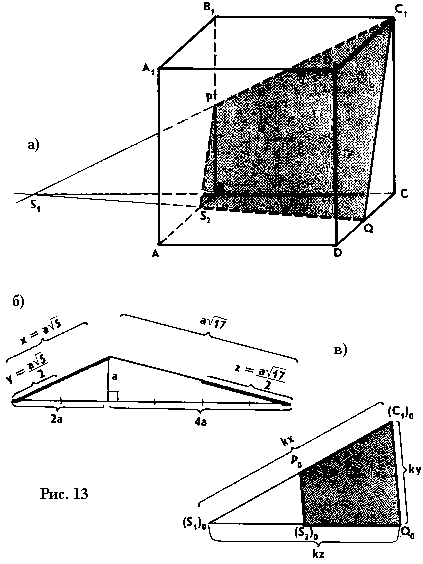
Решение (рис. 13, а). Находим точку S1, в которой пересекаются прямые C1P и BC. Таким образом, прямая S1Q является основным следом плоскости C1PQ, а в сечении получается четырехугольник C1PS1Q.
I способ построения – вычислительный. Полагая ребро куба равным a, подсчитаем стороны треугольника C1S1Q. Как нетрудно показать, точка Р – середина отрезка C1S1 и PS2║ C1Q. Поэтому ясно, что, построив треугольник, подобный оригиналу треугольника C1S1Q, можно будет затем построить и искомую фигуру.
Из прямоугольного треугольника C1S1С, в котором C1S=2ВС=2 a, находим, что C1S1= a √5. Затем из прямоугольного треугольника C1СQ получаем C1Q=½ a √5 и из прямоугольного треугольника CS1Q: S1Q=½ a √17.
Выбирая теперь некоторый отрезок в качестве отрезка, равного а, построим отрезки x, y, z, заданные следующими формулами: x= a √5, y= ½ a √5, z= ½ a √17, например, так, как это сделано ни рисунке 13, б.
Далее на рисунке13, в строим треугольник (С1)0Q0(S1)0 со сторонами (С1)0(S1)0 = kx, (S1)0Q0= kz, полученными на рисунке13, б.
Строим затем точку P0 – середину стороны (C1)0(S1)0 этого треугольника и проводим через нее прямую P0(S1)0║(C1)0Q0. Четырехугольник (С1)0Q0(S2)0P0 – фигура, подобная заданному сечению куба плоскостью C1РQ (т. е. это выносной чертеж многоугольника, являющегося сечением куба плоскостью C1РQ).
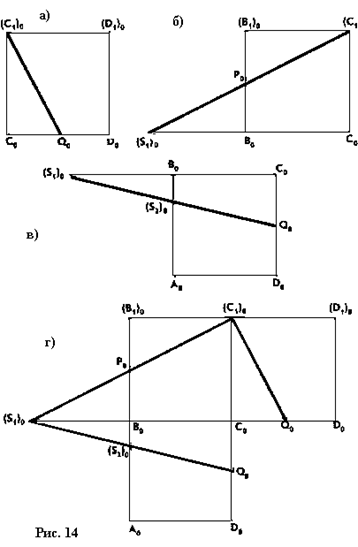 |
II способ – геометрический. Так как все квадраты подобны между собой, то квадрат (С1)0С0D0(D1)0 (рис. 14, а) подобен оригиналу грани C1CDD1 куба. Построив на этом изображении точку Q0 – середину стороны C0D0 и соединив точки (С1)0 и Q0, получим отрезок (С1)0Q0, который можно принять за сторону треугольника (С1)0Q0(S1)0, подобного оригиналу треугольника C1QS1. С помощью квадрата (С1)0C0B0(B1)0 (рис. 14, б), равного квадрату (С1)0C0D0(D1)0, построенному на рисунке 14, а, строим отрезок (С1)0(S1)0, который будет принят за сторону треугольника (С1)0Q0(S1)0, подобно оригиналу треугольника C1QS1.
|
|
|
С помощью квадрата A0B0C0D0 (рис. 14, в), равного квадрату, построенному на рисунке 14, а, строим отрезок (S1)0Q0, который примем за третью сторону треугольника (С1)0Q0(S1)0. Получив, таким образом, все стороны треугольника (С1)0Q0(S1)0, строим этот треугольник. Далее, как и при вычислительном способе решения, строим точку Р0 – середину стороны (S1)0(C1)0 и т. д.
Рисунки а, б, в можно объединить в один рисунок, например, в рисунок г. Так как треугольник (С1)0Q0(S1)0 строится с точностью до подобия, то его сторонами являются отрезки, равные k (С1)0(S1)0, k (С1)0Q0 и k (S1)0Q0, где k >0, например, k =1.
|
|
|


