 |
Уравнения с разделяющимися переменными и однородные дифференциальные уравнения
|
|
|
|
Дифференциальные уравнения 1-го порядка, допускающие представление в виде
= f(x)g(t)
называются дифференциальными уравнениями с разделяющимися переменными. Общий интеграл этого уравнения имеет вид
К уравнениям с разделяющимися переменными могут быть приведены и уравнения вида Х= f(at + bx). Вводя замену z=at+bx. Получим
Рассмотрим дифференциальное уравнение вида
(4.2)
часто принимаемое в первом приближении при исследовании различных процессов. Уравнение выражает тот факт, что скорость изменения функции пропорциональна самой функции. При k>0 уравнение (4.2) описывает процесс размножения бактерий в питательной среде - закон органического роста, характерный для всевозможных цепных реакций. К такой же модели приводит задача о нарастании вклада в сберегательной кассе. При k<0 уравнение (4.2) описывает процесс радиоактивного распада, падения атмосферного давления с высотой, процесс разрядки конденсатора через сопротивление и др. Разделяя переменные, находим у = Сеkx. Решение, удовлетворявшее начальным условиям уо= у(хо), имеет вид у=yоek(x-xo). При k>0 формула показывает экспоненциальное нарастание величины у. При к<0 экспоненциальное убывание. Таким образом, решение уравнения (4.2) позволяет полностью охарактеризовать изучаемый процесс.
Пример1. Найти общий интеграл уравнения
(3+ех)уу’=ех
Реш ение.
Это уравнение является уравнением с разделяющимися переменными
Разделяем переменные
Интегрируя левую часть этого уравнения по у,а правую по х, получим общий интеграл исходного дифференциального уравнения
Дифференциальное уравнение первого порядка называется однородным, если его можно привести к виду
|
|
|
или М(x,y)dx + N(x,y)dy = 0,
где М(x,y) и N(x,y) – однородные функции одного порядка, т.е. существует такое m, что
M(tx,ty) = tmM(x,y) и N(tx,ty) = tmN(x,y).
С помощью подстановки y=tx, где t=t(x), однородные уравнения преобразуются в уравнения с разделяющимися переменными. К однородным уравнениям приводятся уравнения вида
Если 
то полагая x = u + a, y = v + b (постоянные a и b определяются из системы уравнений a1a+b1b+c1=0, a2a+b2b+c=0),
получим однородное дифференциальное уравнение относительно
переменных u и v. При 
получим уравнение с разделяющимися переменными.
Пример 1. Решить уравнение
.
Р е ш е н и е. Запишем уравнение в виде
.
Так как уравнение однородное, то положим 
или y = ux. Тогда 
. Подставляя в уравнение выражение для y и 
, получим
- 
.
Разделяем переменные:
.
Отсюда интегрированием находим
(С1 > 0) или 
.
Так как 
, то обозначая 
, получим
,
где 
или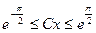 
. Заменяя u на 
, будем иметь общий интеграл:
.
Отсюда общее решение будет: 
.
При разделении переменных мы делили обе части уравнения на произведение 
, поэтому могли поте
решения, которые обращают в нуль его сомножители. Положим теперь x = 0 и 
. Но x = 0 не является решением уравнения, а из второго получаем, что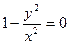 
, откуда 
. Непосредственной проверкой убеждаемся, что функции y = - x и y = x являются решениями уравнения. Функции y = - x и y = x являются особыми решениями данного уравнения.
Пример 2. Решить уравнение
. (1)
Р е ш е н и е. Рассмотрим систему линейных алгебраических уравнений:
.
Определитель этой систем:
.
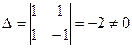Система имеет единственное решение 
, 
. Делаем замену 
, 
.
Тогда уравнение (1) примет вид
(2)
Уравнение (2) является однородным уравнением. Полагая 
, получим
(x + x u)dx + (x - x u)(x du + u dx) = 0
Откуда
(1 + 2u – u2)dx + x (1 - u)du = 0.
|
|
|
Разделяем переменные
.
Интегрируя, найдём
; 
.
Возвращаемся к переменным x, y:
или
.
Пример 3. Решить уравнение
.
Р е ш е н и е. Система линейных алгебраических уравнений
несовместна. Определитель системы
В этом случае метод, применённый в предыдущем примере, не проходит. Для интегрирования уравнения применяем подстановку
x + y = z, dy = dz – dx.
Уравнение примет вид
(2 – z) dx + (2 z – 1) dz = 0.
|
|
|
