 |
Системы дифференциальных уравнений.
|
|
|
|
3 .1.Основные понятия и определения.
Системой дифференциальных уравнений называется совокупность дифференциальных уравнений, каждое из которых содержит независимую переменную, функцию и ее производные.
Система m дифференциальных уравнений с m неизвестными называется канонической, если она разрешена относительно старших производных.
Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
 , (1.1)
, (1.1)
называется нормальной.
Если в канонической системе, содержащей производные произвольного порядка
 ,
,
принять  за новые вспомогательные функции, то общую каноническую систему (1.2) можно заменить эквивалентной ей нормальной системой, состоящей из за новые вспомогательные функции, то общую каноническую систему (1.2) можно заменить эквивалентной ей нормальной системой, состоящей из  уравнений. Поэтому достаточно рассматривать лишь нормальные системы.
Например, одно уравнение уравнений. Поэтому достаточно рассматривать лишь нормальные системы.
Например, одно уравнение  является частным случаем канонической системы. Положив является частным случаем канонической системы. Положив  , в силу исходного уравнения будем иметь , в силу исходного уравнения будем иметь  . В результате получаем нормальную систему уравнений . В результате получаем нормальную систему уравнений
 эквивалентную исходному уравнению.
Определение. Решением нормальной системы (1.1) на интервале (a,b) изменения аргумента t называется всякая система n функций
эквивалентную исходному уравнению.
Определение. Решением нормальной системы (1.1) на интервале (a,b) изменения аргумента t называется всякая система n функций
 (1.2)
дифференцируемых на интервале (1.2)
дифференцируемых на интервале  , обращающая уравнения системы (1.1) в тождества по t на интервале (а,b).
Задача Коши для системы (1.1) формулируется так: найти решение (1.2) системы при начальных условиях , обращающая уравнения системы (1.1) в тождества по t на интервале (а,b).
Задача Коши для системы (1.1) формулируется так: найти решение (1.2) системы при начальных условиях
 (1.3)
Теорема 1.1 (существования и единственности
решения задачи Коши). Пусть имеем нормальную систему дифференциальных уравнений (1.3)
Теорема 1.1 (существования и единственности
решения задачи Коши). Пусть имеем нормальную систему дифференциальных уравнений
 (1.1)
и пусть функции (1.1)
и пусть функции  определены в некоторой (n+1)-мерной области D изменения переменных определены в некоторой (n+1)-мерной области D изменения переменных 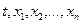 . Если существует окрестность . Если существует окрестность  точки точки  , в которой функции , в которой функции  непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным  , то найдется интервал , то найдется интервал  изменения t, на котором существует единственное решение нормальной системы (1.1), удовлетворяющее начальным условиям (1.3).
Определение. Система n функций изменения t, на котором существует единственное решение нормальной системы (1.1), удовлетворяющее начальным условиям (1.3).
Определение. Система n функций
 (1.4)
зависящих от t и n производных постоянных (1.4)
зависящих от t и n производных постоянных  , называется общим решением нормальной системы (1.1) в некоторой области , называется общим решением нормальной системы (1.1) в некоторой области  существования и единственности решения задачи Коши, если
1) при любых допустимых значениях существования и единственности решения задачи Коши, если
1) при любых допустимых значениях  система функций (1.4) обращает уравнения (1.1) в тождества,
2) в области система функций (1.4) обращает уравнения (1.1) в тождества,
2) в области  функции (1.4) решают любую задачу Коши.
Решения, получающиеся из общего при конкретных значениях постоянных функции (1.4) решают любую задачу Коши.
Решения, получающиеся из общего при конкретных значениях постоянных  , называются частными решениями. Обратимся для наглядности к нормальной системе двух уравнений: , называются частными решениями. Обратимся для наглядности к нормальной системе двух уравнений:
 (1.5)
Будем рассматривать систему значений (1.5)
Будем рассматривать систему значений  как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат  . Решение . Решение 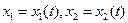 системы (1.5), принимающее при системы (1.5), принимающее при  значения значения  определяет в пространстве некоторую линию, проходящую через точку определяет в пространстве некоторую линию, проходящую через точку  . Эта линия
через данную точку . Эта линия
через данную точку  . Теорема 1.1 устанавливает существование и единственность такой кривой.
3.2. Интегрирование нормальных систем
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной, . Теорема 1.1 устанавливает существование и единственность такой кривой.
3.2. Интегрирование нормальных систем
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной,
 Введя новые функции
Введя новые функции  , заменим это уравнение следующей нормальной системой n уравнений: , заменим это уравнение следующей нормальной системой n уравнений:
 (2.1)
одно уравнение n-го порядка эквивалентно нормальной системе (2.1).
Можно утверждать и обратное, что, вообще говоря, нормальная система n уравнений первого порядка (1.1) эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений. Поясним этот метод на примере. Пусть требуется проинтегрировать систему (2.1)
одно уравнение n-го порядка эквивалентно нормальной системе (2.1).
Можно утверждать и обратное, что, вообще говоря, нормальная система n уравнений первого порядка (1.1) эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений. Поясним этот метод на примере. Пусть требуется проинтегрировать систему
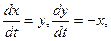 (2.2).
Дифференцируя первое уравнение системы, имеем (2.2).
Дифференцируя первое уравнение системы, имеем  откуда, используя второе уравнение, получаем откуда, используя второе уравнение, получаем  — линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной
неизвестной функцией. Его общее решение имеет вид — линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной
неизвестной функцией. Его общее решение имеет вид
 В силу первого уравнения системы находим функцию
В силу первого уравнения системы находим функцию
 Найденные функции,как легко проверить, при любых значениях С1, С 2 удовлетворяют заданной системе.
3.3 Системы линейных дифференциальных уравнений.
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
Найденные функции,как легко проверить, при любых значениях С1, С 2 удовлетворяют заданной системе.
3.3 Системы линейных дифференциальных уравнений.
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
 (3.1)
в матричной форме – (3.1)
в матричной форме –
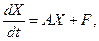 (3.2)
где (3.2)
где  Теорема 3.1. Если все функции
Теорема 3.1. Если все функции  и и  , ,  непрерывны на отоезке непрерывны на отоезке  , то в достаточно малой окрестности каждой точки , то в достаточно малой окрестности каждой точки  , где , где 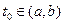 , выполнены условия теоремы существования и единственности решения задачи Коми и, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (3.1).
Действительно, в таком случае правые части системы (3.1) непрерывны по совокупности аргументов , выполнены условия теоремы существования и единственности решения задачи Коми и, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (3.1).
Действительно, в таком случае правые части системы (3.1) непрерывны по совокупности аргументов 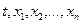 и
частные производные по и
частные производные по  ограничены, так как эти производные равны непрерывным на отрезке [a, b] коэффициентам ограничены, так как эти производные равны непрерывным на отрезке [a, b] коэффициентам  .
Введем линейный оператор .
Введем линейный оператор
 .
Тогда система (3.2) коротко запишется в виде .
Тогда система (3.2) коротко запишется в виде
 (3.3)
Если матрица F — нулевая, т. е. (3.3)
Если матрица F — нулевая, т. е.  на интервале (а, b), то система (3.1) называется линейной однородной и имеет вид на интервале (а, b), то система (3.1) называется линейной однородной и имеет вид
 (3.4)
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема 3.2. Если X(t) является решением линейной однородной системы L[X] = 0, то сХ(t), где с — произвольная постоянная, является решением той же системы.
Теорема 3.3. Сумма (3.4)
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема 3.2. Если X(t) является решением линейной однородной системы L[X] = 0, то сХ(t), где с — произвольная постоянная, является решением той же системы.
Теорема 3.3. Сумма  двух решений двух решений  u u  однородной линейной системы уравнений является решением той же системы.
Следствие. Линейная комбинация однородной линейной системы уравнений является решением той же системы.
Следствие. Линейная комбинация  с произвольными постоянными коэффициентами с произвольными постоянными коэффициентами  решений решений  линейной однородной системы дифференциальных уравнений линейной однородной системы дифференциальных уравнений  является решением той же системы.
Теорема 3.4. Если является решением той же системы.
Теорема 3.4. Если  есть решение линейной неоднородной системы есть решение линейной неоднородной системы 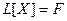 , а , а  — решение соответствующей однородной системы — решение соответствующей однородной системы  , то сумма , то сумма 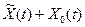 будет решением неоднородной системы будет решением неоднородной системы
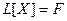 .
Действительно, по условию, .
Действительно, по условию,  . Пользуясь свойством аддитивности оператора L, получаем . Пользуясь свойством аддитивности оператора L, получаем
 Это означает, что сумма
Это означает, что сумма  есть решение неоднородной системы уравнений есть решение неоднородной системы уравнений  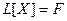 .
Определение. Векторы .
Определение. Векторы  , где , где
 ,
называются линейно зависимыми на интервале ,
называются линейно зависимыми на интервале  , если существуют постоянные числа , если существуют постоянные числа  такие, что такие, что
 (3.5)
при (3.5)
при  , причем по крайней мере одно из чисел , причем по крайней мере одно из чисел  не равно нулю. Если тождество (3.5) справедливо только при не равно нулю. Если тождество (3.5) справедливо только при  , то векторы , то векторы  называются линейно независимыми на называются линейно независимыми на  .
Заметим, что одно векторное тождество (3.5) эквивалентно n тождествам: .
Заметим, что одно векторное тождество (3.5) эквивалентно n тождествам:
 (3.5’)
Определитель (3.5’)
Определитель
 называется определителем Вронского системы векторов
называется определителем Вронского системы векторов  .
Определение. Пусть имеем линейную однородную систему .
Определение. Пусть имеем линейную однородную систему
 (3.6)
где (3.6)
где 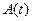 — —  -матрица с элементами -матрица с элементами  . Система n решений . Система n решений  линейной однородной системы (3.4), линейно независимых на интервале линейной однородной системы (3.4), линейно независимых на интервале  , называется фундаментальной.
Теорема 3.5. Определитель Вронского , называется фундаментальной.
Теорема 3.5. Определитель Вронского  фундаментальной на интервале фундаментальной на интервале  системы решений линейной однородной системы (3.4) с непрерывными на
отрезке системы решений линейной однородной системы (3.4) с непрерывными на
отрезке  коэффициентами коэффициентами  отличен от нуля во всех точках интервала отличен от нуля во всех точках интервала  .
Теорема 3.6. (о структуре общего решения линейной однородной системы). Общим решением в области .
Теорема 3.6. (о структуре общего решения линейной однородной системы). Общим решением в области  , ,  , ,  , линейной однородной системы , линейной однородной системы
 (3.7)
с непрерывными на отрезке (3.7)
с непрерывными на отрезке  коэффициентами коэффициентами  является линейная комбинация n линейно независимых на интервале является линейная комбинация n линейно независимых на интервале  решений решений  системы (3.7): системы (3.7):
 (
( — произвольные постоянные числа).
Например, система — произвольные постоянные числа).
Например, система
 имеет, как нетрудно проверить, решения
имеет, как нетрудно проверить, решения
 Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
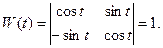 Общее решение системы имеет вид
Общее решение системы имеет вид
 или или  (
( — произвольные постоянные).
Квадратная матрица — произвольные постоянные).
Квадратная матрица
 столбцами которой являются линейно независимые решения
столбцами которой являются линейно независимые решения  системы (3.7), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению системы (3.7), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению  .
Если .
Если  — фундаментальная матрица системы (3.7), то общее решение системы можно представить в виде — фундаментальная матрица системы (3.7), то общее решение системы можно представить в виде
 (3.8)
где (3.8)
где  —постоянная матрица-столбец с произвольными элементами. Полагая в (3.8) —постоянная матрица-столбец с произвольными элементами. Полагая в (3.8)  , имеем , имеем
 , откуда , откуда  ;
следовательно, ;
следовательно,  .
Матрица .
Матрица 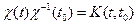 называется матрицей Коши. С ее помощью решение системы (3.7) можно представить так: называется матрицей Коши. С ее помощью решение системы (3.7) можно представить так:
 Теорема 3.7 (о структуре общего решения линейной неоднородной системы дифференциальных уравнений). Общее решение в области
Теорема 3.7 (о структуре общего решения линейной неоднородной системы дифференциальных уравнений). Общее решение в области  , ,  , ,  , линейной неоднородной системы дифференциальных уравнений , линейной неоднородной системы дифференциальных уравнений
 (3.2)
с непрерывными на отрезке (3.2)
с непрерывными на отрезке  коэффициентами коэффициентами  и правыми частями и правыми частями  равно сумме общего решения равно сумме общего решения  соответствующей однородной системы и какого-нибудь частного решения соответствующей однородной системы и какого-нибудь частного решения  неоднородной системы (3.2): неоднородной системы (3.2):
 .
3.4. Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений .
3.4. Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
 в которой все коэффициенты
в которой все коэффициенты  — постоянные. Проще всего такая система интегрируется
сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Будем искать решение системы — постоянные. Проще всего такая система интегрируется
сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Будем искать решение системы
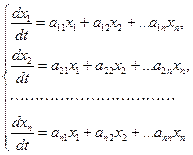 (4.1)
в виде (4.1)
в виде
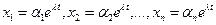 , (4.2)
где , (4.2)
где 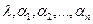 — постоянные. Подставляя — постоянные. Подставляя  в форме (4.2) в систему (4.1), сокращая на в форме (4.2) в систему (4.1), сокращая на  и перенося все члены в одну часть равенства, получаем систему и перенося все члены в одну часть равенства, получаем систему
 (4.3)
Для того чтобы эта система (4.3) линейных однородных алгебраических уравнений с n неизвестными (4.3)
Для того чтобы эта система (4.3) линейных однородных алгебраических уравнений с n неизвестными 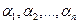 имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:
имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:
 (4.4)
Уравнение (4.4) называется характеристическим. В его левой части стоит многочлен относительно (4.4)
Уравнение (4.4) называется характеристическим. В его левой части стоит многочлен относительно  степени n. Из этого уравнения определяются те значения степени n. Из этого уравнения определяются те значения  , при которых система (4.3) имеет нетривиальные решения , при которых система (4.3) имеет нетривиальные решения 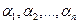 . Если все корни . Если все корни  характеристического уравнения (4.4) различные, то, подставляя их по очереди в систему (4.3), находим соответствующие им нетривиальные решения характеристического уравнения (4.4) различные, то, подставляя их по очереди в систему (4.3), находим соответствующие им нетривиальные решения 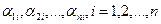 , этой системы и, следовательно, находим n решений исходной системы дифференциальных уравнений (4.1) в виде , этой системы и, следовательно, находим n решений исходной системы дифференциальных уравнений (4.1) в виде
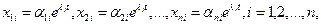 (4.5)
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом решений линейной однородной системы (4.1) (4.5)
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом решений линейной однородной системы (4.1)
 (4.6)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (4.1) имеет вид (4.6)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (4.1) имеет вид
 или
или
 где
где  — произвольные постоянные.
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример 4.1. Решить систему — произвольные постоянные.
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример 4.1. Решить систему
 Ищем решение в виде
Ищем решение в виде  .
Характеристическое уравнение .
Характеристическое уравнение
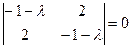 или или  имеет корни
имеет корни  Система (3.3) для определения
Система (3.3) для определения  выглядит так: выглядит так:
 (*)
Подставляя в (*) (*)
Подставляя в (*)  , получаем , получаем
 откуда откуда 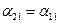 .
Следовательно, .
Следовательно,  ,
Полагая в (*) ,
Полагая в (*)  , находим , находим  , поэтому , поэтому
 .
Общее решение данной системы: .
Общее решение данной системы:
 или или 
| |
3.5. Решение систем дифференциальных уравнений методом интегрируемых комбинаций.
Этот метод интегрирования систем дифференциальных уравнений (не обязательно линейных) состоит в следующем: посредствам подходящих арифметических операций (например, сложение, вычитание др.) из уравнений заданной системы образуют так называемые интегрируемые комбинации, то есть достаточно просто интегрируемые уравнения вида
 ,
где u – некоторая функция от искомых функций x1(t), x2(t),…,xn(t).
Пример 1. Решить систему ,
где u – некоторая функция от искомых функций x1(t), x2(t),…,xn(t).
Пример 1. Решить систему
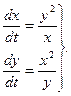 (2)
Решение. Перепишем систему (2) в виде (2)
Решение. Перепишем систему (2) в виде
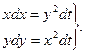 (3)
Сложив почленно, получим (3)
Сложив почленно, получим
 - 72 -
или
- 72 -
или
 откуда
откуда
 Потенцируя, будем иметь
Потенцируя, будем иметь
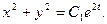 (4)
Вычитая почленно из первого уравнения (3) второе, получим (4)
Вычитая почленно из первого уравнения (3) второе, получим
 или
или
 отсюда
отсюда
 (5)
Разрешая (4) и (5) относительно x и y найдём общее решение системы (2): (5)
Разрешая (4) и (5) относительно x и y найдём общее решение системы (2):
 где для упрощения записи положено
где для упрощения записи положено
  .
Пример 2.Найти частное решение системы .
Пример 2.Найти частное решение системы
 (6)
удовлетворяющее начальным условиям (6)
удовлетворяющее начальным условиям
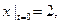  (7)
Решение. Умножив первое уравнение на 2 и сложив со вторым, получим (7)
Решение. Умножив первое уравнение на 2 и сложив со вторым, получим
 отсюда
отсюда
 (8)
Подставляя (8) в первое уравнение (6), получаем линейное уравнение для определения x: (8)
Подставляя (8) в первое уравнение (6), получаем линейное уравнение для определения x:
 (9)
Отсюда (9)
Отсюда
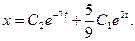 (10)
Следовательно, (10)
Следовательно,
 (11)
Выражение (10) и (11) представляют общее решение системы (6).
Чтобы найти частное решение, удовлетворяющее условию (7), надо в (10) и (11) вместо t, x и y подставить соответственно числа 0, 2 и 5. Получим систему уравнений для определения C1 и C2: (11)
Выражение (10) и (11) представляют общее решение системы (6).
Чтобы найти частное решение, удовлетворяющее условию (7), надо в (10) и (11) вместо t, x и y подставить соответственно числа 0, 2 и 5. Получим систему уравнений для определения C1 и C2:
 (12)
откуда (12)
откуда
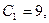  Ответ:
Ответ: 
| |
3.Системы дифференциальных уравнений.
3.1.Основные понятия и определения.
Системой дифференциальных уравнений называется совокупность дифференциальных уравнений, каждое из которых содержит независимую переменную, функцию и ее производные.
Система m дифференциальных уравнений с m неизвестными называется канонической, если она разрешена относительно старших производных.
Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
 , (1.1)
называется нормальной.
Если в канонической системе, содержащей производные произвольного порядка , (1.1)
называется нормальной.
Если в канонической системе, содержащей производные произвольного порядка
 , , 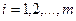 (1.2)
принять (1.2)
принять  за новые вспомогательные функции, то общую каноническую систему (1.2) можно заменить эквивалентной ей нормальной системой, состоящей из за новые вспомогательные функции, то общую каноническую систему (1.2) можно заменить эквивалентной ей нормальной системой, состоящей из  уравнений. Поэтому достаточно рассматривать лишь нормальные системы.
Например, одно уравнение уравнений. Поэтому достаточно рассматривать лишь нормальные системы.
Например, одно уравнение  является частным случаем канонической системы. Положив является частным случаем канонической системы. Положив  , в силу исходного уравнения будем иметь , в силу исходного уравнения будем иметь  . В результате получаем нормальную систему уравнений . В результате получаем нормальную систему уравнений
 эквивалентную исходному уравнению.
Определение. Решением нормальной системы (1.1) на интервале (a,b) изменения аргумента t называется всякая система n функций
эквивалентную исходному уравнению.
Определение. Решением нормальной системы (1.1) на интервале (a,b) изменения аргумента t называется всякая система n функций
 (1.2)
дифференцируемых на интервале (1.2)
дифференцируемых на интервале  , обращающая уравнения системы (1.1) в тождества по t на интервале (а,b).
Задача Коши для системы (1.1) формулируется так: найти решение (1.2) системы при начальных условиях , обращающая уравнения системы (1.1) в тождества по t на интервале (а,b).
Задача Коши для системы (1.1) формулируется так: найти решение (1.2) системы при начальных условиях
 (1.3)
Теорема 1.1 (существования и единственности решения задачи Коши). Пусть имеем нормальную систему дифференциальных уравнений (1.3)
Теорема 1.1 (существования и единственности решения задачи Коши). Пусть имеем нормальную систему дифференциальных уравнений
 (1.1)
и пусть функции (1.1)
и пусть функции  определены в некоторой (n+1)-мерной области D изменения переменных определены в некоторой (n+1)-мерной области D изменения переменных 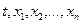 . Если существует окрестность . Если существует окрестность  точки точки  , в которой функции , в которой функции  непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным  , то найдется интервал , то найдется интервал  изменения t, на котором существует единственное решение нормальной системы (1.1), удовлетворяющее начальным условиям (1.3).
Определение. Система n функций изменения t, на котором существует единственное решение нормальной системы (1.1), удовлетворяющее начальным условиям (1.3).
Определение. Система n функций
 (1.4)
зависящих от t и n производных постоянных (1.4)
зависящих от t и n производных постоянных  , называется общим решением нормальной системы (1.1) в некоторой области , называется общим решением нормальной системы (1.1) в некоторой области  существования и единственности решения задачи Коши, если
3) при любых допустимых значениях существования и единственности решения задачи Коши, если
3) при любых допустимых значениях  система функций (1.4) обращает уравнения (1.1) в тождества,
4) в области система функций (1.4) обращает уравнения (1.1) в тождества,
4) в области  функции (1.4) решают любую задачу Коши.
Решения, получающиеся из общего при конкретных значениях постоянных функции (1.4) решают любую задачу Коши.
Решения, получающиеся из общего при конкретных значениях постоянных  , называются частными решениями. Обратимся для наглядности к нормальной системе двух уравнений: , называются частными решениями. Обратимся для наглядности к нормальной системе двух уравнений:
 (1.5)
Будем рассматривать систему значений (1.5)
Будем рассматривать систему значений  как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат  . Решение . Решение 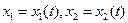 системы (1.5), принимающее при системы (1.5), принимающее при  значения значения  определяет в пространстве некоторую линию, проходящую через точку определяет в пространстве некоторую линию, проходящую через точку  . Эта линия называется интегральной кривой нормальной системы (1.5).
Задача Коши для системы (1.5) получает следующую геометрическую формулировку: в пространстве переменных . Эта линия называется интегральной кривой нормальной системы (1.5).
Задача Коши для системы (1.5) получает следующую геометрическую формулировку: в пространстве переменных  найти интегральную кривую, проходящую через данную точку найти интегральную кривую, проходящую через данную точку  . Теорема 1.1 устанавливает существование и единственность такой кривой.
3.2. Интегрирование нормальных систем
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной, . Теорема 1.1 устанавливает существование и единственность такой кривой.
3.2. Интегрирование нормальных систем
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной,
 Введя новые функции
Введя новые функции  , заменим это уравнение следующей нормальной системой n уравнений: , заменим это уравнение следующей нормальной системой n уравнений:
 (2.1)
одно уравнение n-го порядка эквивалентно нормальной системе (2.1).
Можно утверждать и обратное, что, вообще говоря, нормальная система n уравнений первого порядка (1.1) эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений. Поясним этот метод на примере. Пусть требуется проинтегрировать систему (2.1)
одно уравнение n-го порядка эквивалентно нормальной системе (2.1).
Можно утверждать и обратное, что, вообще говоря, нормальная система n уравнений первого порядка (1.1) эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений. Поясним этот метод на примере. Пусть требуется проинтегрировать систему
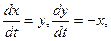 (2.2).
Дифференцируя первое уравнение системы, имеем (2.2).
Дифференцируя первое уравнение системы, имеем  откуда, используя второе уравнение, получаем откуда, используя второе уравнение, получаем  — линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной
неизвестной функцией. Его общее решение имеет вид — линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной
неизвестной функцией. Его общее решение имеет вид
 В силу первого уравнения системы находим функцию
В силу первого уравнения системы находим функцию
 Найденные функции,как легко проверить, при любых значениях С1, С 2 удовлетворяют заданной системе.
3.3 Системы линейных дифференциальных уравнений.
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
Найденные функции,как легко проверить, при любых значениях С1, С 2 удовлетворяют заданной системе.
3.3 Системы линейных дифференциальных уравнений.
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
 (3.1)
в матричной форме – (3.1)
в матричной форме –
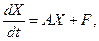 (3.2)
где (3.2)
где  Теорема 3.1. Если все функции
Теорема 3.1. Если все функции  и и  , ,  непрерывны на отоезке непрерывны на отоезке  , то в достаточно малой окрестности каждой точки , то в достаточно малой окрестности каждой точки  , где , где 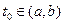 , выполнены условия теоремы существования и единственности решения задачи Коми и, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (3.1).
Действительно, в таком случае правые части системы (3.1) непрерывны по совокупности аргументов , выполнены условия теоремы существования и единственности решения задачи Коми и, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (3.1).
Действительно, в таком случае правые части системы (3.1) непрерывны по совокупности аргументов 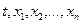 и
частные производные по и
частные производные по  ограничены, так как эти производные равны непрерывным на отрезке [a, b] коэффициентам ограничены, так как эти производные равны непрерывным на отрезке [a, b] коэффициентам  .
Введем линейный оператор .
Введем линейный оператор
 .
Тогда система (3.2) коротко запишется в виде .
Тогда система (3.2) коротко запишется в виде
 (3.3)
Если матрица F — нулевая, т. е. (3.3)
Если матрица F — нулевая, т. е.  на интервале (а, b), то система (3.1) называется линейной однородной и имеет вид на интервале (а, b), то система (3.1) называется линейной однородной и имеет вид
 (3.4)
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема 3.2. Если X(t) является решением линейной однородной системы L[X] = 0, то сХ(t), где с — произвольная постоянная, является решением той же системы.
Теорема 3.3. Сумма (3.4)
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема 3.2. Если X(t) является решением линейной однородной системы L[X] = 0, то сХ(t), где с — произвольная постоянная, является решением той же системы.
Теорема 3.3. Сумма  двух решений двух решений  u u  однородной линейной системы уравнений является решением той же системы.
Следствие. Линейная комбинация однородной линейной системы уравнений является решением той же системы.
Следствие. Линейная комбинация  с произвольными постоянными коэффициентами с произвольными постоянными коэффициентами  решений решений  линейной однородной системы дифференциальных уравнений линейной однородной системы дифференциальных уравнений  является решением той же системы.
Теорема 3.4. Если является решением той же системы.
Теорема 3.4. Если  есть решение линейной неоднородной системы есть решение линейной неоднородной системы 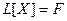 , а , а  — решение соответствующей однородной системы — решение соответствующей однородной системы  , то сумма , то сумма 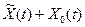 будет решением неоднородной системы будет решением неоднородной системы
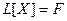 .
Действительно, по условию, .
Действительно, по условию,  . Пользуясь свойством аддитивности оператора L, получаем . Пользуясь свойством аддитивности оператора L, получаем
 Это означает, что сумма
Это означает, что сумма  есть решение неоднородной системы уравнений есть решение неоднородной системы уравнений  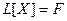 .
Определение. Векторы .
Определение. Векторы  , где , где
 ,
называются линейно зависимыми на интервале ,
называются линейно зависимыми на интервале  , если существуют постоянные числа , если существуют постоянные числа  такие, что такие, что
 (3.5)
при (3.5)
при  , причем по крайней мере одно из чисел , причем по крайней мере одно из чисел  не равно нулю. Если тождество (3.5) справедливо только при не равно нулю. Если тождество (3.5) справедливо только при  , то векторы , то векторы  называются линейно независимыми на называются линейно независимыми на  .
Заметим, что одно векторное тождество (3.5) эквивалентно n тождествам: .
Заметим, что одно векторное тождество (3.5) эквивалентно n тождествам:
 (3.5’)
Определитель (3.5’)
Определитель
 называется определителем Вронского системы векторов
называется определителем Вронского системы векторов  .
Определение. Пусть имеем линейную однородную систему .
Определение. Пусть имеем линейную однородную систему
 (3.6)
где (3.6)
где 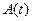 — —  -матрица с элементами -матрица с элементами  . Система n решений . Система n решений  линейной однородной системы (3.4), линейно независимых на интервале линейной однородной системы (3.4), линейно независимых на интервале  , называется фундаментальной.
Теорема 3.5. Определитель Вронского , называется фундаментальной.
Теорема 3.5. Определитель Вронского  фундаментальной на интервале фундаментальной на интервале  системы решений линейной однородной системы (3.4) с непрерывными на
- 64 -
отрезке системы решений линейной однородной системы (3.4) с непрерывными на
- 64 -
отрезке  коэффициентами коэффициентами  отличен от нуля во всех точках интервала отличен от нуля во всех точках интервала  .
Теорема 3.6. (о структуре общего решения линейной однородной системы). Общим решением в области .
Теорема 3.6. (о структуре общего решения линейной однородной системы). Общим решением в области  , ,  , ,  , линейной однородной системы , линейной однородной системы
 (3.7)
с непрерывными на отрезке (3.7)
с непрерывными на отрезке  коэффициентами коэффициентами  является линейная комбинация n линейно независимых на интервале является линейная комбинация n линейно независимых на интервале  решений решений  системы (3.7): системы (3.7):
 (
( — произвольные постоянные числа).
Например, система — произвольные постоянные числа).
Например, система
 имеет, как нетрудно проверить, решения
имеет, как нетрудно проверить, решения
 Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
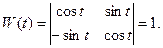 Общее решение системы имеет вид
Общее решение системы имеет вид
 или или  (
( — произвольные постоянные).
Квадратная матрица — произвольные постоянные).
Квадратная матрица
 столбцами которой являются линейно независимые решения
столбцами которой являются линейно независимые решения  системы (3.7), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению системы (3.7), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению  .
Если .
Если  — фундаментальная матрица системы (3.7), то общее решение системы можно представить в виде — фундаментальная матрица системы (3.7), то общее решение системы можно представить в виде
 (3.8)
где (3.8)
где  —постоянная матрица-столбец с произвольными элементами. Полагая в (3.8) —постоянная матрица-столбец с произвольными элементами. Полагая в (3.8) | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользуйтесь поиском по сайту:

©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...

