 |
Понятие о линейной зависимости строк и столбцов матрицы Теорема о ранге матрицы.
|
|
|
|
Теорема 1.
Определитель равен сумме произведений всех элементов, какой-нибудь строки (столбца) на их алгебраическое дополнение.
Теорема 2.
Сумма произведений всех элементов какой-нибудь строки (столбца) определителя на алгебраическое дополнение соответствующих элементов другой строки (столбца) равна 0.
4. Определитель произведения матриц. Определение обратной матрицы. Доказать теорему существования и единственности обратной матрицы.
Квадратная матрица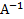 
называется обратной для матрицы А того же порядка, если их произведение равно единичной матрицы.
5. Алгоритм нахождения обратной матрицы. Матричные уравнения АХ=В, YA=B.
Алгоритм нахождения обратной матрицы с помощью союзной матрицы:
1) Убеждаемся, что матрица А квадратная и её определить отличен от 0.
· Если окажется, что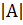 
=0, то обратной матрицы для матрицы А не существует.
· Если 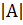≠0, то Ǝ (!) 
2) Составим матрицу из алгебраических дополнений.
3) Составим союзную матрицу.
Системы линейных алгебраических уравнений. Основные понятия. Матричная запись. Правило Крамера.
Если хотя бы одно из чисел системы отличных от нуля -система не вырождена, если все правые части системы равны 0,то система является однородной.
Решение системы называется совокупность значений a1,a2,a3 Удовлетворяющей всей системы одновременно
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
правило Крамера -применяется только для квадратных матриц (определитель отличный от нуля)и имеет только одно решение
Ранг матрицы. Элементарные преобразования матрицы. Методы нахождения ранга матрицы.
|
|
|
Рангом матрицы называется наивысший из порядков миноров этой матрицы, определитель которых отличен от нуля
Если ранг=n что среди минора порядка n найдется хотя бы один отличный от 0. Порядка r+1 и выше будут равны 0 либо не существовать.
Ранг матрица равен количеству нулевых строк после приведения к ступенчатому виду.
Две матрицы называются эквивалентными получаются из другого с помощью прибавления конечных множителей. Эквивалентными не являются равными, но их ранги равны
1 способ:
Метод окаймления миноров
Если минор 
-го порядка не равен нулю, а все миноры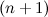 
-го равны нулю, то ранг матрицы будет равен .
2 способ:
Элементарные преобразования
Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю
Элементарные преобразования матрицы не изменяют её ранг.
Ранг матрица равен количеству нулевых строк после приведения к ступенчатому виду.
Понятие о линейной зависимости строк и столбцов матрицы Теорема о ранге матрицы.
Система из k столбцов A1,A2,…,AkA1,A2,…,Ak
называется линейно независимой, если равенство α1⋅A1+α2⋅A2+…+αk⋅Ak=o возможно только при
α1=α2=…=αk=0α1=α2=…=αk=0
|
|
|
, т.е. когда линейная комбинация в левой части тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).
1. Один столбец A1тоже образует систему: при A1=0
— линейно зависимую, а при A1≠0 линейно независимую.
2. Любая часть системы столбцов называется подсистемой.
Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А).
|
|
|
