 |
Условия параллельности и перпендикулярности двух плоскостей.
|
|
|
|
В случае перпендикулярности двух плоскостей

угол между ними равен 90°, т. е. cos φ=0. Поэтому из формулы  имеем условие перпендикулярности плоскостей:
имеем условие перпендикулярности плоскостей:

Замечание. Это условие получится сразу, если заметим, что скалярное произведение нормальных векторов 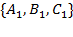 и
и  должно быть равно нулю.
должно быть равно нулю.
Условие параллельности плоскостей в векторной форме может быть записано так:  где
где  и
и  обозначают векторы, перпендикулярные к данным плоскостям. Переходя к проекциям, перепишем это условие таким образом:
обозначают векторы, перпендикулярные к данным плоскостям. Переходя к проекциям, перепишем это условие таким образом:

что равносильно условию

Замечание. Условие без векторов можно установить так в случае параллельности плоскостей.Имеем:

Заменяя здесь косинусы их выражениями через коэффициенты уравнений  , получим:
, получим:

откуда находим:

Обратно, если выполнено условие, то плоскости параллельны. В самом деле, уравнения этих плоскостей будут:
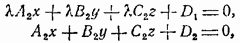
где λ обозначает величину каждого отношения равенств. Деля первое уравнение на λ, получим:

Следовательно, выполняются соотношения, и плоскости параллельны.
Кароче, Склифосовский!
(короткая версия билета 52)
Если две плоскости  и
и  заданы общими уравнениями вида:
заданы общими уравнениями вида:

Под углом между плоскостями  и и  понимается один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между понимается один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между 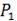 и и  равен углу между их нормалями, то есть между векторами равен углу между их нормалями, то есть между векторами  1 1  и и  2 2  . Из формулы . Из формулы  получаем, что косинус угла между плоскостями получаем, что косинус угла между плоскостями 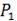 и и  равен равен 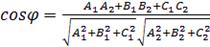 . .
|
Условие параллельности плоскостей (рис.б) заключается в параллельности нормалей 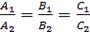 , а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:
, а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:  .
.
Векторно-параметрическое уравнение прямой в пространств. Каноническое уравнение прямой.
|
|
|
Векторное уравнение прямой. Параметрические уравнения прямой.
Положение прямой в пространстве вполне определяется заданием какой-либо ее фиксированной точки  и вектора s, параллельного этой прямой. Вектор s, параллельный прямой, называется направляющим вектором этой прямой, а его проекции на координатные оси — направляющими коэффициентами прямой.
и вектора s, параллельного этой прямой. Вектор s, параллельный прямой, называется направляющим вектором этой прямой, а его проекции на координатные оси — направляющими коэффициентами прямой.
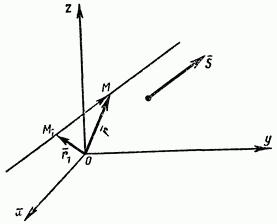
Рис. 86
Пусть прямая L задана ее точкой  и направляющим вектором
и направляющим вектором  имеющим направляющие коэффициенты m, n и p.
имеющим направляющие коэффициенты m, n и p.
Рассмотрим произвольную точку  на прямой. Из рис. 86 непосредственно получаем
на прямой. Из рис. 86 непосредственно получаем
 (13)
(13)
Вектор 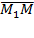 , лежащий на прямой L, параллелен направляющему вектору s, поэтому
, лежащий на прямой L, параллелен направляющему вектору s, поэтому
 (14)
(14)
где скалярный множитель называемый параметром, может принимать любое значение в зависимости от положения точки М на прямой. Обозначая радиусы-векторы точек  и М соответственно через
и М соответственно через  ,
,  и принимая во внимание формулу (14), запишем уравнение (13) в виде
и принимая во внимание формулу (14), запишем уравнение (13) в виде
 (15)
(15)
Уравнение (15) называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.
Представим уравнение (15) в координатной форме. Замечая, что

получим

Уравнения (16) называются параметрическими уравнениями прямой. При изменении параметра t изменяются координаты x, y, z и точка  перемещается по прямой.
перемещается по прямой.
Канонические уравнения прямой
Пусть  - точка, лежащая на прямой L, и
- точка, лежащая на прямой L, и  - направляющий вектор прямой. Вектор
- направляющий вектор прямой. Вектор  ,, соединяющий точку М, с переменной точкой
,, соединяющий точку М, с переменной точкой  прямой L, параллелен вектору s (см. рис. 86). Поэтому проекции векторов МХМ и s пропорциональны. Так как
прямой L, параллелен вектору s (см. рис. 86). Поэтому проекции векторов МХМ и s пропорциональны. Так как  , то
, то
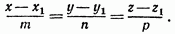 (17)
(17)
Итак, координаты любой точки прямой должны удовлетворять уравнениям (17), которые называются уравнениями прямой, проходящей через данную точку, или каноническими уравнениями прямой.

Рис. 87
В частном случае, когда направляющий вектор s — единичный,  , уравнения (17) имеют следующий вид:
, уравнения (17) имеют следующий вид:
|
|
|
 (18)
(18)
|
|
|


