Предел и непрерывность функции

Федеральное агентство по образованию Российской Федерации

Филиал Санкт-Петербургского государственного морского

Технического университета

СЕВМАШВТУЗ

 

Аксенова Н.М. Минин М.В.

ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ

ИСЧИСЛЕНИЕ ФУНКЦИИ

ОДНОЙ ПЕРЕМЕННОЙ

Учебное пособие

 

Северодвинск

УДК 512

 

Аксенова Н.М., Минин М.В. Дифференциальное и интегральное исчисление функции одной переменной: Учебное пособие. – Северодвинск: РИО Севмашвтуза, 2006. – 50 с.

 

 

Ответственный редактор доцент Н.М. Аксенова

 

 

Рецензенты: к.ф.-м.н., доцент кафедры Математики Севмашвтуза

Н.Д. Самышкина;

зав. кафедрой Экономики и финансов филиала СЗАГС,

к.т.н., доцент Н.И. Черенков.

 

Учебное пособие предназначено для студентов заочной формы обучения специальности 080502 «Экономика», изучающих курс высшей математики. Пособие рассчитано на второй семестр обучения, включает в себя теоретический и практический материал по дифференциальному и интегральному исчислению функции одной переменной. В учебное пособие входит две контрольные работы, задачи с решениями для успешного усвоения изложенного материала.

 

 

ISBN 5-7723-0615-4

© Севмашвтуз, 2006 г.

 

 

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ............................................................................................................. 4

1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 5

1.1. Основные понятия...................................................................................... 5

1.2. Предел и непрерывность функции............................................................ 5

1.3. Производная............................................................................................ 11

1.4. Дифференциал функции........................................................................... 13

1.5. Производные высших порядков............................................................. 16

1.6. Формула Лагранжа.................................................................................. 16

1.7. Необходимые и достаточные условия экстремума функции................. 17

1.8. Выпуклость и вогнутость функции......................................................... 19

1.9. Асимптоты графика функции.................................................................. 21

2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ 23

2.1. Неопределенный интеграл....................................................................... 23

2.2. Замена переменной в неопределенном интеграле.................................. 25

2.3. Формула интегрирования по частям...................................................... 26

2.4. Определенный интеграл.......................................................................... 28

2.5. Определенный интеграл как функция верхнего предела....................... 30

2.6. Несобственные интегралы с бесконечными пределами......................... 33

КОНТРОЛЬНАЯ РАБОТА №3............................................................................ 34

Пример выполнения задания:............................................................................ 39

КОНТРОЛЬНАЯ РАБОТА №4............................................................................ 43

Пример выполнения задания:............................................................................ 47

СПИСОК ЛИТЕРАТУРЫ.................................................................................... 49

ВВЕДЕНИЕ

Учебное пособие курса «Дифференциальное и интегральное исчисление функций одной переменной» составлено для студентов заочной формы обучения специальности 080502 «Экономика» (II семестр).

Настоящее пособие разработано в соответствии с требованиями Государственного стандарта Министерства образования РФ 2000 года подготовки специалистов специальности экономист-менеджер.

Издание данного учебного пособия вызвано необходимостью систематизации теоретического и практического материала и так же особенностью обучения по заочной форме. Студентам удобнее и проще разобраться в учебном пособии, в котором сконцентрированы основные понятия, определения, методы и приемы решения типовых задач.

Учебное пособие содержит контрольные работы №3 и №4 (30 вариантов).

Приведены примеры подробного решения каждой контрольной работы.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Основные понятия

Пусть D — некоторое множество чисел. Если задан закон, по которому каждому числу x из множества D ставится в соответствие единственное определенное число y, то будем говорить, что на множестве D задана функция, которую назовём f. Число y — это значение функции f в точке x, что обозначается формулой y = f(x).

Число x называется аргументом функции, множество D — областью определения функции, а все значения y образуют множество E, которое называется множеством значений или областью изменения функции.

Функция f называется возрастающей (убывающей) на множестве G, если для любых чисел х ₁ и х ₂ из множества G, таких что x ₁ < x ₂, выполняется условие f (x ₁) < f (x ₂) (f (x ₁) > f (x ₂)).

Так как между множеством действительных чисел и множеством точек числовой оси можно установить взаимно-однозначное соответствие, в дальнейшем изложении понятиям “число х ”и “точка х числовой оси” в некоторых случаях будет придаваться один и тот же смысл. Например, вместо “значение функции при значении аргумента, равном х ₁” будет говориться “значение функции в точке х ₁”. В нижеследующем опре­делении можно везде заменить выражение “точка х ” на выражение “число х ”.

Пусть e — некоторое положительное число. e -окрестностью точки x ₀ называется множество всех точек x, принадлежащих промежутку (x ₀ ‑ e, x ₀ + e). Принадлежность точки x e ‑ окрестности точки можно выразить с помощью двойного неравенства

.

Число eназывается радиусом окрестности.

Предел и непрерывность функции

Рассмотрим функцию y = x ² в точке x ₀ = 2. Значение функции в этой точке равно 4.

Отметим одну особенность поведения функции в этой точке. Можно

выбрать какое-либо поло­жительное число eи построить e - окрестность точки y ₀ = 4. Очевидно, что найдется такая окрестность точки x ₀ = 2 (на рисунке 1 эта окрестность имеет радиус d), что если x будет лежать в этой окрестности, то соответствующее значение y, равное x ², попадет в e - окрестность точки y ₀ = 4. Это заключение справедливо для любого, сколь угодно малого числа e. Здесь точка x ₀ = 2 выбрана произвольно. Можно было бы для данной функции выбрать любую другую точку и сделать подобное заключение.

Рассмотрим функцию . Эта функция не определена в точке x ₀ = 2. При x ₀ ¹ 2 её можно преобразовать:

.

График функции представлен на рисунке 2. Хотя исходная функция не определена в точке x ₀ = 2 и естественно не равна 3 в этой точке, точка y ₀ = 3 имеет характерную особенность. Выбрав положитель­ное число e, можно утверждать, что если рассматривать значения x, расположенные достаточно близко к точке x ₀ = 2 (или лежащие в некоторой окрестности точки x ₀ = 2, причем радиус этой окрестности зависит от e), то соответствующие значения y попадут в e-окрестность точки y ₀ = 3. Всё сказанное остаётся справедливым независимо от того, насколько малым выбрано положительное число e.

Введем понятие предела функции. Число A называется пределом функции y = f (x) в точке x ₀ (иногда говорят, при x, стремящемся к x ₀), если для любого положительного числа e можно найти такое положительное число d, что для всех x из d - окрестности точки x ₀, за исключением самой точки x ₀ соответствующие значения y попадают в e - окрестность точки y = A.

Можно сформулировать определение предела функции по-другому. Число A называется пределом функции y = f (x) в точке x ₀, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию

0 < ê x – x ₀ê < d,

выполняется условие

ê y – A ê < e.

Тот факт, что A есть предел функции y = f (x) в точке x = x ₀, записывается

так:

.

Как видно из второго из рассмотренных выше примеров, для того, чтобы функция имела предел в точке x = x ₀, не требуется, чтобы она была определена в этой точке.

Рассмотрим функцию . Очевидно, что если x > 0, то y = 2 ^x; если x < 0, то y = – 2 ^x; при x = 0 функция не определена.

График функции изображен на рисунке 3. Легко убедиться в том, что, согласно приведенному выше определению предела, эта функция в точке x = 0 предела не имеет.

Функция y = f (x) называется непрерывной в точке x = x ₀, если она определена в некоторой окрестности этой точки и ее значение f (x ₀) равно пределу функции в этой точке: .

Функция y = x ² непрерывна в точке x = 2, как и во всех точках числовой оси. Функция не является непрерывной в точке x = 2. Функция не является непрерывной в точке x = 0.

Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.

Приведем свойства предела функции.

1. Функция не может иметь в одной точке два разных предела.

2. , если C — постоянная функция.

3. Если существует и C — постоянная функция, то

.

4. Если существуют и , то существует , равный , а также существует , равный . Если при этом , то существует , равный .

Введем определения так называемых “односторонних пределов”.

Число B называется пределом функции f (x) в точке a справа (это записывается в виде формулы ), если для любого поло­жительного числа e найдется положительное число d, такое что из из условия 0 < x – a < d будет следовать .

Согласно приведенному определению . Отметим, что обычного предела функция в точке x = 0 не имеет.

Число С называется пределом функции f (x) в точке b слева (это записывается в виде формулы ), если для любого поло­жительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать ê C – f (x)ê < e.

Очевидно, что функция (её график, изображен на рисунке 3) имеет два односторонних предела в точке x = 0:

; .

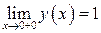Функция f (x) называется непрерывной в точке a справа (непрерывной в точке b слева), если

().

Функция непрерывна справа в точке x =0.

Функция называется непрерывной на замкнутом промежутке [ a, b ], если она непрерывна на открытом промежутке (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

Достаточно просто можно доказать теорему, связывающую понятия предела функции в точке и односторонних пределов. Мы ограничимся только формулировкой теоремы.

Для того, чтобы выполнялось равенство , необходимо и достаточно, чтобы одновременно выполнялись два равенства:

;

В дальнейшем нам понадобятся понятия предела функции в бесконечно удалённых точках. Рассмотрим сначала функцию f (x), определенную на полубесконечном промежутке . Число А называется пределом функции f (x) при х, стремящемся к плюс бесконечности:

,

если для любого положительного числа e можно найти такое положительное число M (зависящее от e), ч то для всех чисел х, превосходящих М, выполняется условие:

½ f (x) – A ½ < e.

Пусть теперь функция f (x) определена на полубесконечном промежутке
(–¥; х ₀). Число А называется пределом функции f (x) при х, стремящемся к минус бесконечности:

,

если для любого положительного числа e можно найти такое положительное число M (зависящее от e), ч то для всех чисел х, меньших, чем – М, выполняется условие:

½ f (x) – A ½ < e.

Отметим два, так называемых, "замечательных предела".

1. . Геометрический смысл этой формулы заключается в том, что прямая является касательной к графику функции в точке .

2. . Здесь e — иррациональное число, приблизительно равное 2,72.

Приведем пример применения понятия предела функции в экономических расчетах. Рассмотрим обыкновенную финансовую сделку: предоставление в долг суммы S ₀ с условием, что через период времени T будет возвращена сумма S_T. Определим величину r относительного роста формулой

. (1)

Относительный рост можно выразить в процентах, умножив полученное значение r на 100.

Из формулы (1) легко определить величину S_T:

S_T = S ₀(1 + r)

При расчете по долгосрочным кредитам, охватывающим несколько полных лет, используют схему сложных процентов. Она состоит в том, что если за 1-й год сумма S ₀ возрастает в (1 + r) раз, то за второй год в (1 + r) раз возрастает сумма S ₁ = S ₀(1 + r), то есть S ₂ = S ₀(1 + r)². Аналогично получается S ₃ = S ₀(1 + r)³. Из приведенных примеров можно вывести общую формулу для вычисления роста суммы за n лет при расчете по схеме сложных процентов:

S_n = S ₀(1 + r) ⁿ.

В финансовых расчетах применяются схемы, где начисление сложных процентов производится несколько раз в году. При этом оговариваются годовая ставка r и количество начислений за год k. Как правило, начисления производятся через равные промежутки времени, то есть длина каждого промежутка T_k составляет часть года. Тогда для срока в T лет (здесь T не обязательно является целым числом) сумма S_T рассчитывается по формуле

(2)

Здесь — целая часть числа , равная ближайшему к наименьшему целому числу.

Пусть годовая ставка равна r и производится n начислений в год через равные промежутки времени. Тогда за год сумма S ₀ наращивается до величины, определяемой формулой

(3)

В теоретическом анализе и в практике финансовой деятельности часто встречается понятие “непрерывно начисляемый процент”. Чтобы перейти к непрерывно начисляемому проценту, нужно в формулах (2) и (3) неограниченно увеличивать соответственно, числа k и n (то есть устремить k и n к бесконечности) и вычислить, к какому пределу будут стремиться функции S_T и S ₁. Применим эту процедуру к формуле (3):

.

Заметим, что предел в фигурных скобках совпадает со вторым замечательным пределом. Отсюда следует, что при годовой ставке r при непрерывно начисляемом проценте сумма S ₀ за 1 год наращивается до величины S ₁^*, которая определяется из формулы

. (4)

Пусть теперь сумма S ₀ предоставляется в долг с начислением процента n раз в год через равные промежутки времени. Обозначим r_e годовую ставку, при которой в конце года сумма S ₀ наращивается до величины S ₁^* из формулы (4). В этом случае будем говорить, что r_e — это годовая ставка при начислении процента n раз в год, эквивалентная годовому проценту r при непрерывном начислении. Из формулы (3) получаем

.

Приравнивая правые части последней формулы и формулы (4), полагая в последней T = 1, можно вывести соотношения между величинами r и r_e:

, .

Эти формулы широко используются в финансовых расчётах.

Производная

Рассмотрим функцию y=f (x), непрерывную в некоторой окрестности точки x. Пусть D x  приращение аргумента в точке x. Обозначим через Dy или D f приращение функции, равное f (x +D x) – f (x). Отметим здесь, что функция непрерывна в точке x, если в этой точке бесконечно малому прира­щению аргу­мента D x соответствует беско­нечно малое приращение функции D f.

Отношение D f /D x, как видно из рисунка 4, равно тангенсу угла a, который составляет секущая MN кривой y = f (x) c положительным направлением горизонтальной оси координат.

Представим себе процесс, в котором величина D x, неограниченно уменьшаясь, стремится к нулю. При этом точка N будет двигаться вдоль кривой y = f (x), приближаясь к точке M, а секущая MN будет вращаться около точки M так, что при очень малых величинах D x её угол наклона a будет сколь угодно близок к углу j наклона касательной к кривой в точке x. Следует отметить, что все сказанное относится к случаю, когда график функции y = f (x) не имеет излома или разрыва в точке x, то есть в этой точке можно провести касательную к графику функции.

Отношение D y / D x или, что то же самое (f (x + D x)  f (x)) / D x, можно рассматривать при заданном x как функцию аргумента D x. Эта функция не определена в точке D x = 0. Однако её предел в этой точке может существовать.

Если существует предел отношения (f (x + D x) – f (x)) / D x в точке D x = 0, то он называется производной функции y = f (x)в точке x и обозначается y¢ или f¢ (x):

.

Нахождение производной функции y = f (x)называется дифференцированием.

Если для любого числа x из открытого промежутка (a, b) можно вычислить f¢ (x), то функция f (x) называется дифференцируемой на промежутке (a, b).

Геометрический смысл производной заключается в том, что произ­водная функции f (x)в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.

Производная  это скорость изменения функции в точке x. Из определения производной следует, что f¢ (x)» D f / D x, причем точность этого приближенного равенства тем выше, чем меньше D x. Производная f¢ (x) является приближенным коэффициентом пропорциональности между D f и D x.

Производная функции f (x) не существует в тех точках, в которых функция не является непрерывной. В то же время функция может быть непрерывной в точке x ₀, но не иметь в этой точке производной. Такую точку назовём угловой точкой графика функции или точкой излома. Графические примеры приведены на рисунке 5.

 

Так функция y = ê x ê не имеет производной в точке x = 0, хотя является непрерывной в этой точке.

Ниже приводится таблица производных элементарных функций.

 

 

f (x)		f (x)		f (x)

Приведем теперь основные свойства производной.

1. Если функция имеет производную в точке, то она непрерывна в этой точке.

2. Если существует f¢ (x), и С ‑ произвольное число, то функция имеет производную: (Cf (x)) ¢ = Cf¢ (x).

3. Если существуют f¢ (x)и g¢ (x), то функция S (x) = f (x) + g (x) имеет производную: S¢ (x) = f¢ (x) + g¢ (x).

4. Если существуют f¢ (x) и g¢ (x), то функция P (x) = f (x) g (x) имеет производную: P¢ (x) = f¢ (x) g (x) + f (x) g¢ (x).

5. Если существуют f¢ (x) и g¢ (x) и при этом g (x) ¹ 0, то функция D (x) = f (x) / g (x) имеет производную: D¢ (x) = (f¢ (x) g (x)  f (x) g¢ (x)) / g ²(x).

В любом курсе математического анализа доказывается теорема о производной сложной функции. Мы ограничимся лишь ее формулировкой.

Пусть функция g (x) имеет производную в точке x, а функция f (z) имеет производную в точке z = g (x). Тогда сложная функция F (x) = f (g(x))имеет в точке x производную F¢ (x) = f¢ (z) g ¢ (x).

Приведем примеры вычисления производной сложной функции.

Дифференциал функции

Рассмотрим две функции: y ₁ = f ₁(x) и y ₂ = f ₂(x), которые имеют производные f ₁ ¢ (x) и f ₂ ¢ (x) в каждой точке некоторой области D. Возьмем какую-либо точку x из области D и дадим аргументу приращение D x. Тогда функции получат соответственно приращения D y ₁ = f ₁(x + D x)  f ₁(x) и D y ₂ = f ₂(x + D x)  f ₂(x). Из графиков, изображенных на рисунке 6, видно, что в обоих случаях приращения D y ₁ и D y ₂ можно представить в виде сумм двух слагаемых:

D y ₁ = (C ₁ - A ₁) + (B ₁ - C ₁); D y ₂ = (C ₂ - A ₂) + (B ₂ - C ₂) (5)

Рис. 6

Первые слагаемые в правых частях обоих выражений (5) легко вычисляются из сходных формул: C ₁ – A ₁ = tg a ₁ D x = f ₁ ¢ (x)D x; C ₂ – A ₂ = tg a ₂ D x = f ₂ ¢ (x)D x.

Величина f¢ (x) D x называется главной частью приращения функции y = f (x) в точке x. (Здесь мы говорим только о функции, имеющей в точке x производную). Главная часть приращения функции линейна относительно приращения аргумента D x (можно сказать – пропор­циональна приращению D x). Это означает, что если приращение аргумента D x уменьшить в k раз, то и главная часть приращения функции уменьшится в k раз.

Формулы (5) можно переписать в виде:

D y ₁ = f ₁ ¢ D x + r ₁; Dy ₂ = f ₂ ¢ D x + r ₂. (6)

Здесь r ₁ = B ₁ – C ₁; r ₂= B ₂– C ₂.

Величины r ₁ и r ₂ в формулах (6) при уменьшении D x в k раз уменьшаются более чем в k раз, что можно видеть, сравнивая рисунки 6 и 7, и говорят, что r ₁ и r ₂ стремятся к нулю быстрее, чем D x.

Рис. 7

Назовем функцию бесконечно малой в точке z = z ₀, если .

Пусть функции и являются бесконечно малыми в точке z = z ₀. Функция называется бесконечно малой более высокого порядка, чем функция , если .

Величины r ₁ и r ₂ в формулах (2) являются функциями аргумента D x, бесконечно малыми в точке D x = 0. Можно показать, что . Это означает, что функции r ₁(D x) и r ₂(D x) являются бесконечно малыми функциями более высокого порядка, чем D x, в точке D x = 0.

Таким образом приращение функции y = f (x)в точке, в которой существует её производная, может быть представлено в виде

D y = f¢ (x) D x +b (D x),

где b (D x) ‑ бесконечно малая функция более высокого порядка, чем D x, в точке D x = 0.

Главная, линейная относительно D x,часть приращения функции y = f (x), равная f¢ (x) D x, называется дифференциалом и обозначается dy:

dy = f¢ (x) D x. (7)

Если сюда подставить функцию f (x) = x, то, так как x¢ = 1, формула (7) примет вид: dx = D x. Эта формула легко истолковывается с помощью графика функции y = x, из которого видно, что приращение этой функции содержит лишь главную часть. Таким образом, для функции y = x приращение совпадает с дифференциалом. Теперь формулу дифференциала (7) можно переписать так

dy = f¢ (x) dx.

Отсюда следует, что

,

то есть производная функции f (x) равна отношению дифференциала функции к дифференциалу аргумента x.

Очевидны следующие свойства дифференциала.

1. (здесь и в следующей формуле C  постоянная);

2. ;

3. Если существуют df (x) и dg (x), то d (f (x) + g (x)) = df (x) + dg (x), 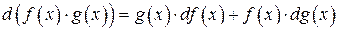. Если при этом g (x) ¹0, то

Пусть y = f (x) ‑ функция, имеющая производную в точке x, тогда dy = df (x) = f¢ (x) dx. Если аргумент x является функцией x (t) некоторой независимой переменной t, то y = F (t) = f (x (t)) сложная функция от t, и её дифференциал вычисляется по формуле 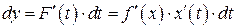. Однако по определению дифференциала x¢ (t) dt = dx и последняя формула преобразуется к виду: dy = f¢ (x) dx.

Таким образом если аргумент функции y=f (x)рассматривать как функцию другого аргумента так, что равенство D x = dx не выполняется, формула дифференциала функции f (x) остается неизменной. Это свойство принято называть свойством инвариантности дифференциала.

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: