 |
Несобственные интегралы с бесконечными пределами
|
|
|
|
Если положить промежуток интегрирования бесконечным, то приведенное выше определение определенного интеграла теряет смысл, например, потому что невозможно осуществить условия n ®¥; l®0 для бесконечного промежутка. Для такого интеграла требуется специальное определение.
Пусть функция y = f (x) определена и непрерывна на полубесконечном промежутке [ a;¥), тогда несобственным интегралом с бесконечным пределом  называется
называется  , если предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
, если предел существует. Если этот предел не существует, то не существует и несобственный интеграл. В этом случае принято говорить, что несобственный интеграл расходится. При существовании предела говорят, что несобственный интеграл сходится.
Аналогично
 и
и  .
.
Примеры: 1.  . Очевидно:
. Очевидно:  , откуда следует
, откуда следует
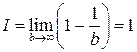 .
.
2.  ; этот предел не существует, следовательно, не существует или расходится интеграл I.
; этот предел не существует, следовательно, не существует или расходится интеграл I.
3.  ; здесь предел также не существует, и интеграл расходится.
; здесь предел также не существует, и интеграл расходится.
КОНТРОЛЬНАЯ РАБОТА №3
Задание:
1. Вычислить предел функции, используя свойства пределов.
2. Вычислить предел функции, используя первый замечательный предел.
3. Вычислить предел функции, используя второй замечательный предел.
4. Найти производную функции  , заданной явным образом.
, заданной явным образом.
5. Найти производную  функции
функции  , заданной параметрически.
, заданной параметрически.
6. Для функции 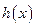 найти производную указанного порядка.
найти производную указанного порядка.
7. Исследовать функцию  и построить ее график.
и построить ее график.
Варианты заданий представлены в таблице 1.
Таблица 1
| 1 вариант | 2 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 3 вариант | 4 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 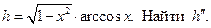
|
| 7. | 
| 7. | 
|
| 5 вариант | 6 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 7 вариант | 8 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 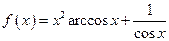
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 9 вариант | 10 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 11 вариант | 12 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 13 вариант | 14 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 15 вариант | 16 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 17 вариант | 18 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 19 вариант | 20 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 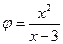
|
| 21 вариант | 22 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 23 вариант | 24 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 25 вариант | 26 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 27 вариант | 28 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
| 29 вариант | 30 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 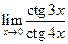
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7. | 
| 7. | 
|
|
|
|
Пример выполнения задания:
1. 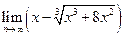
В данном случае имеем неопределенность вида « ». Перенесем иррациональность в знаменатель, умножая и деля исходное выражение на такой множитель, чтобы получить разность кубов, т.е.
». Перенесем иррациональность в знаменатель, умножая и деля исходное выражение на такой множитель, чтобы получить разность кубов, т.е.  . Этот множитель есть неполный квадрат суммы:
. Этот множитель есть неполный квадрат суммы:  . Получим:
. Получим:

2. 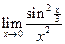
Обозначим  . Следовательно,
. Следовательно,  . При
. При  и
и  . Перейдем к новой переменной:
. Перейдем к новой переменной:
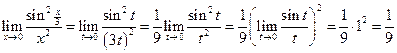
3. 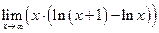
Здесь имеет место неопределенность « ». Для раскрытия этой неопределенности воспользуемся свойствами логарифма
». Для раскрытия этой неопределенности воспользуемся свойствами логарифма  и
и  . Кроме того, для непрерывных логарифмических функций существует правило:
. Кроме того, для непрерывных логарифмических функций существует правило:  . Итак:
. Итак:
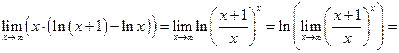
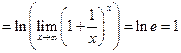
4. 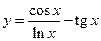
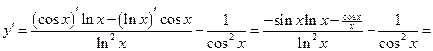
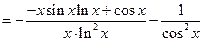
5. 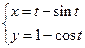
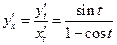
6.  .Найти
.Найти  .
.
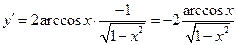
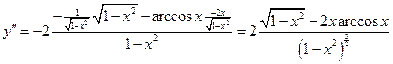
7. 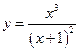
Непосредственное исследование функции:
|
|
|
1)  , так как функция определена всюду, кроме точки
, так как функция определена всюду, кроме точки  .
.
2)  - координата точки пересечения графика с осью
- координата точки пересечения графика с осью  . Эта точка
. Эта точка  - единственная точка пересечения графика с осями координат.
- единственная точка пересечения графика с осями координат.
При  имеем
имеем  ; при
; при  , т.е. график лежит в первой и третьей четвертях.
, т.е. график лежит в первой и третьей четвертях.
3)  - точка разрыва;
- точка разрыва;  , значит, прямая
, значит, прямая  есть вертикальная асимптота, а точка
есть вертикальная асимптота, а точка  - точка разрыва второго рода.
- точка разрыва второго рода.
4) Найдем асимптоты графика при  :
:



Вывод:  - наклонная асимптота графика функции при
- наклонная асимптота графика функции при  .
.
Исследование функции с помощью первой производной:
1)  .
.
2) Найдем нули производной, решив уравнение  , т.е.:
, т.е.:
 .
.
Получим:  ;
;  .
.
3) Результаты исследования запишем в таблицу (см. таблицу 2):
Таблица 2

| 
| 
| 
| 
| 
| 
|

| + | – | + | + | ||

| 
| 
| 
| 
| 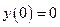 экстремума нет экстремума нет
| 
|
Вывод: функция возрастает на каждом из промежутков  ,
,  и
и  и убывает на
и убывает на  .
.  - точка максимума, так как при переходе через эту точку и возрастании
- точка максимума, так как при переходе через эту точку и возрастании  производная меняет знак с плюса на минус.
производная меняет знак с плюса на минус.
Исследование функции с помощью второй производной:
1) 
 .
.
2) Найдем точки, в которых  :
:
 .
.
3) Результаты занесем в таблицу (см. таблицу 3):
Таблица 3

| 
| 
| 
| |

| – | – | + | |

| 
| 
|  , ,  . 0 – точка перегиба . 0 – точка перегиба
| 
|
 - есть точка перегиба графика, так как при переходе через эту точку
- есть точка перегиба графика, так как при переходе через эту точку  меняет знак.
меняет знак.
Построим график функции, используя найденные данные (см. рис. 24):
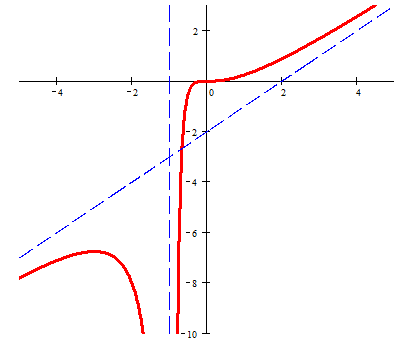
(Рис. 24)
КОНТРОЛЬНАЯ РАБОТА №4
Задание:
1. Найти неопределенный интеграл.
2. Найти неопределенный интеграл.
3. Найти неопределенный интеграл.
4. Вычислить определенный интеграл.
5. Найти площадь фигуры, ограниченной указанными линиями.
6. Вычислить несобственный интеграл или установить его расходимость.
Варианты заданий представлены в таблице 4.
Таблица 4
| 1 вариант | 2 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 3 вариант | 4 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 5 вариант | 6 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 7 вариант | 8 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 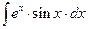
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 9 вариант | 10 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 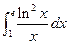
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 11 вариант | 12 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 13 вариант | 14 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 15 вариант | 16 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 17 вариант | 18 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 19 вариант | 20 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 21 вариант | 22 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 23 вариант | 24 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 25 вариант | 26 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | 
| 3. | 
|
| 4. | 
| 4. | 
|
| 5. | 
| 5. | 
|
| 6. | 
| 6. | 
|
| 27 вариант | 28 вариант | ||
| 1. | 
| 1. | 
|
| 2. | 
| 2. | 
|
| 3. | |||
|
|
|
|
|
|


