Окончательные выводы корреляционного анализа

Совместный анализ поля корреляции и окончательного значения выборочного коэффициента парной линейной корреляции (r _yx = 0,98) позволяет сделать следующие выводы:

1. Есть зависимость выхода нитробензола от времени его синтеза (в изученном диапазоне времени), т.е. время реакции оказывает влияние на выход нитробензола.

2. Данная зависимость с вероятностью 0,95 является корреляционной линейной.

3. Знак зависимости - положительный.

4. Зависимость является очень тесной.

 

5.1.3. Составление планов эксперимента с учетом возможности
проведения корреляционного анализа

Корреляционный анализ не накладывает повышенных требований к планированию эксперимента. Единственным обязательным условием является выполнение соотношения m_j > 2. Из рекомендаций по планированию эксперимента для проведения корреляционного анализа можно привести следующие. Желательно, чтобы план эксперимента предусматривал:

1) широкую область изменения значений факторов x _j;

2) большое число m_j значений (уровней) факторов x _j, при этом разница между уровнями должна быть больше абсолютной погрешности их измерения;

3) повторные опыты для каждого значения факторов x _j;

4) большое общее число измерений (N).

 

5.2. Планирование эксперимента для применения дисперсионного
анализа

5.2.1. Некоторые общие положения дисперсионного анализа

Дисперсионный анализ - это метод математической статистики, который широко применяется в различных отраслях науки как самостоятельно, так и в сочетании с другими методами.

Суть дисперсионного анализа заключается в сравнении между собой двух или более дисперсий и доказательстве нуль-гипотезы разности этих дисперсий.

При установлении зависимости j дисперсионным анализом исходят из следующих соображений.

В эксперименте изменения средних арифметических значений свойства объекта (` y <sub>v</sub>) зависят не только от изменяемых факторов x <sub>j</sub> (с известными уровнями), но и от случайных факторов. Поэтому рассеивание (разброс)` y _v относительно общего среднего арифметического значения (рис. 5), характеризуемое общей дисперсией (), разделяется на составляющие: рассеивание, обусловленное случайными факторами (, , ), и рассеивание, обусловленное известными факторами за счет изменения их значений, т.е. перехода с одного уровня на другие (, и др.). Попарное сравнение всех факторных дисперсий () с дисперсией, характеризующей действие случайных факторов, т.е. воспроизводимость эксперимента (), позволяет на основании закона распределения Фишера сделать следующие основные выводы дисперсионного анализа:

Установить или опровергнуть влияние x _j на y с заданной вероятностью ("влияет", "не влияет" и др.).

Определить вероятность влияния x _j на y.

 

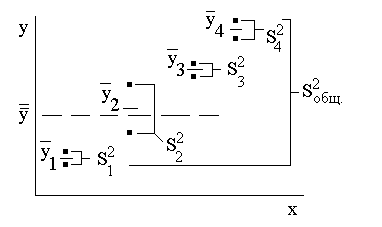
Рис. 5. Поле корреляции величин y и x

 

Так, например, после проведения эксперимента и математической обработки результатов измерений можно вычислить F-отношение (F_p):

; ; .

Задав вероятность (Р) и вычислив по известным формулам числа степеней свободы для факторной дисперсии f_факт. (f₁) и дисперсии воспроизводимости f_воспр. (f₂), из справочных данных выбираем табличное значение квантиля распределения Фишера (F_т). При выполнении неравенства F_P> F_т можно делать вывод, что данный фактор х с вероятностью Р влияет на свойство y, т.е. "значима" разность между влиянием на свойство y известного фактора х и случайных факторов. При невыполнении этого неравенства делается вывод об отсутствии влияния фактора х на свойство y, т.е. это влияние соизмеримо со случайными ошибками эксперимента.

Дисперсионный анализ по сравнению с корреляционным анализом имеет существенные преимущества:

1. Позволяет делать однозначные и более точные выводы о влиянии фактора x _j на свойство y.

2. Позволяет определить влияние на свойство y не только количественных, но и качественных факторов (например, типа растворителя, времени года и др.).

3. Позволяет оценить значение (уровень) фактора x _j, при котором он начинает влиять с заданной вероятностью на свойство y.

Планирование эксперимента для проведения дисперсионного анализа зависит от числа известных факторов, одновременно изменяемых в эксперименте. Различают планы экспериментов для проведения одно-, двух- и многофакторного (трех- и более) дисперсионного анализа.

5.2.2. Составление планов эксперимента для проведения дисперсионного анализа

Общим требованием к планированию любого эксперимента для проведения дисперсионного анализа является выполнение условия
m_j > 1. Желательно, чтобы план эксперимента для проведения дисперсионного анализа предусматривал:

1) широкую область изменения значений факторов x _j,

2) большое число m_j значений (уровней) факторов x _j, при этом разница между уровнями должна быть больше абсолютной погрешности их измерения.

Остальные требования к составлению плана эксперимента зависят от числа исследуемых факторов и выбранного числа опытов.

5.2.2.1. Составление планов экспериментов для проведения однофакторного дисперсионного анализа

Введем следующие обозначения:

А	- исследуемый фактор;
m	- максимальное число разных уровней фактора А;
v	- номер уровня фактора А;
аv	- конкретное значение (качественное или количественное) уровня фактора А (v = 1…m);
n	- максимальное число повторений каждого опыта при одном значении фактора А;
i	- номер повторного опыта при одном значении фактора А;
N	- общее число опытов при эксперименте.

Тогда при одинаковом числе повторений опытов для каждого уровня фактора А:

N = mn.

Классической формой плана для проведения однофакторного дисперсионного анализа является таблица (табл. 8). Условные обозначения уровней фактора часто называют "кодированными" значениями фактора, а реальные значения (качественные или количественные) - натуральными значениями.

Таблица 8

План эксперимента для проведения однофакторного дисперсионного анализа с кодированными значениями уровней фактора А

Номер	Значения y при уровне фактора А
повтор­ного опыта	a1	a2	...	az	...	am-1	am
...
i
...
n-1
n

 

Очевидно, что число пустых клеточек в табл. 8 соответствует общему числу опытов в эксперименте (N). В эти клеточки после проведения соответствующего опыта заносят измеренное значение свойства объекта y.

5.2.2.2. Составление планов экспериментов для проведения двухфакторного дисперсионного анализа

Двухфакторный дисперсионный анализ предусматривает возможность проведения экспериментов без повторения опытов. Если обозначить второй фактор В, максимальное число его уровней w и номер уровня q, то общее число опытов в плане эксперимента без повторения опытов будет равно:

N = mw.

Классический план такого эксперимента (табл. 9) является планом полного факторного эксперимента ( ПФЭ), так как в нем предусмотрены опыты со всеми возможными сочетаниями различных уровней всех факторов.

Более понятным для выполнения является развернутый план эксперимента. Развернутый план получают из классического плана, присвоив в случайном порядке (принцип рандомизации) номера опытов каждой пустой ячейке табл. 9. Условия проведения каждого опыта (табл. 10) определяются исходя из того, какие столбец и строка (уровни фактора А и В) совмещаются в ячейке с данным номером опыта.

Таблица 9
План эксперимента для проведения двухфакторного дисперсионного

анализа с кодированными значениями уровней факторов

Уро­вень	Значения y при уровне фактора А
факто­ра В	a1	a2	...	az	...	am-1	am
b1	№ 8	№ 3	...	№1	...	...	...
b2	...	№5	...	...	...	...	№ 7
...	...	...	...	...	...	...	...
bq	№ 4	...	...	...	...	...	...
...	...	...	...	...	...	...	...
bw-1	№ 2	№ mw	...	...	...	...	...
bw	...	№ 6	...	...	...	...	...

 

Таблица 10

Развернутый план эксперимента для проведения двухфакторного

дисперсионного анализа с кодированными значениями уровней факторов

Номер опыта	Кодированные значения уровня фактора	Значение y
	А	В
	az	b1
	a1	bw-1
	a2	b1
	a1	bq
	a2	b2
	a2	bw
	am	b2
	a1	b1
...	...	...
mw	a2	bw-1

 

Если в плане эксперимента предусмотреть повторение каждого опыта, то тогда при проведении дисперсионного анализа результатов измерений y можно оценить влияние на данное свойство объекта эффекта одновременного изменения двух факторов (эффектов " взаимодействия " факторов). Эффекты взаимодействия могут иметь синергетический (взаимоусили­вающий) или антагонистический (взаимоослабляющий) характер влияния одновременного изменения факторов x _j на свойство y.

5.2.2.3. Составление планов экспериментов для проведения
многофакторного дисперсионного анализа

При многофакторном эксперименте одновременно изменяются три и более факторов. Общее число опытов (без их повторений) для ПФЭ с k изменяемыми факторами (если каждый из них имеет одно и то же максимальное число уровней m) будет равно:

N_ПФЭ= m^k.

Очевидно, что с увеличением числа исследуемых факторов (k) общее число опытов в эксперименте будет резко возрастать. Поэтому при многофакторных экспериментах часто применяют планы дробных факторных экспериментов (ДФЭ), которые предусматривают выполнение опытов только с частью всех возможных сочетаний различных уровней всех факторов. Долю общего числа опытов ДФЭ (N_ДФЭ) от N_ПФЭ называют степенью дробности ДФЭ.

Необходимо помнить, что сокращение числа опытов в эксперименте, т.е. переход от ПФЭ к ДФЭ, всегда приводит к снижению точности дисперсионного анализа результатов эксперимента.

Существуют различные принципы составления и типы планов ДФЭ: составление планов по принципу дробных реплик, латинских квадратов и кубов, планы Плакетта-Бермана и др. Эти планы относятся к планам математического планирования эксперимента, так как при их построении сочетание уровней факторов в опытах (выбор части опытов из планов ПФЭ) происходит не произвольно, а по определенным принципам математической комбинаторики.

Планы ДФЭ широко применяются при отсеивающих экспериментах, т.е. тогда, когда необходимо изучить достаточно большое число факторов при небольшом числе опытов и определить те факторы, которые оказывают наиболее сильное влияние на свойство y. Одними из самых экономичных по числу опытов и эффективных для дисперсионного анализа из известных планов ДФЭ являются планы Плакетта-Бермана.

В качестве примера приведу порядок выбора и составления плана 10-факторного эксперимента (k =10). С целью экономии числа опытов в эксперименте возьмем наименьшее число уровней всех факторов (m_j = m = 2) и откажемся от проведения повторных опытов (n_z,j = n = 1). Тогда для проведения ПФЭ необходимо будет выполнить следующее число опытов:

N_ПФЭ = m^k = 2¹⁰ = 1024.

Из известных 2-уровневых планов ДФЭ оценим число опытов для планов по принципу дробных реплик ПФЭ (ДР) и планов
Пла­кетта-Бермана (ПБ):

N_ДР = 2^k-a = 2^10-a, где а равно 1, 2, 3,...,10 и соответственно N_ДР равно 512, 256, 128, 64, 32, 16, 8, 4, 2, 1;

N_ПБ = 4b, где b равно 1, 2, 3,..., ¥ и соответственно N_ПБ равно 4, 8, 12,... ¥.

Из таких 2-уровневых планов можно выбирать только те, для которых выполняется соотношение:

N ³ k+1 ³ 10+1 ³ 11.

Требованиям этого соотношения и минимального числа опытов лучше всех удовлетворяет план Плакетта-Бермана с N_ПБ = 12. Построим такой план с кодированными факторами, обозначая знаком "+" одно из двух натуральных значений каждого из факторов, а знаком "-" другое значение. Например, примем следующие обозначения (табл. 11).

Таблица 11

Значения факторов

Фактор	Значения факторов
	натуральные (Хj) и их размерность	кодированные (xj)
Время реакции	130 мин	+
	100 мин	-
Тип катализатора	Катализатор № 3	+
	Без катализатора	-
...	...	...
Температура реакции	90ОС	+
	60ОС	-

Тогда план эксперимента типа N_ПБ = 12 (план Плакетта-Бермана) будет следующим (табл. 12).

При построении данного плана в ячейки последнего опыта с
N = k+1(№ 12) заносится кодированное значение (-) для всех факторов. Затем во втором столбце плана (для х ₁) по рекомендациям литературы [8,9] или по случайному принципу в ячейках располагается 6 (k/2) знаков (+) и 5 (k/2-1) знаков (-). Ячейки последующего столбца получаются из предыдущего. Первая ячейка последующего столбца является предпоследней ячейкой предыдущего столбца, а остальные первые k-2 ячейки предыдущего столбца переносятся под первую ячейку последующего столбца (со сдвигом по диагонали плана слева-направо-вниз).

Таблица 12

План эксперимента типа N_ПБ = 12

Но-

Кодированные значения факторов

y

мер

x1

x2

x3

x4

x5

x6

x7

x8

x9

x10

x11

x12

опы-

(*)

(*)

та n

+

-

+

-

-

-

+

+

+

-

+

+

+

+

-

+

-

-

-

+

+

+

-

+

-

+

+

-

+

-

-

-

+

+

+

-

+

-

+

+

-

+

-

-

-

+

+

+

+

+

-

+

+

-

+

-

-

-

+

+

+

+

+

-

+

+

-

+

-

-

-

+

-

+

+

+

-

+

+

-

+

-

-

-

-

-

+

+

+

-

+

+

-

+

-

-

-

-

-

+

+

+

-

+

+

-

+

-

+

-

-

-

+

+

+

-

+

+

-

+

-

+

-

-

-

+

+

+

-

+

+

-

-

-

-

-

-

-

-

-

-

-

-

-

* Фиктивные факторы, используемые для расчета случайных ошибок эксперимента.

 

Правильность построения плана Плакетта-Бермана определяется двумя признаками:

1. Диагональным расположением одинаковых знаков в ячейках плана.

2. Равенством количества знаков (+) и (-) в каждом столбце плана.

План с натуральными значениями факторов получается из плана с кодированными значениями путем замены знаков (+) и (-) на соответствующие им натуральные значения для каждого фактора.

Примеры составления других планов многофакторного ДФЭ для проведения дисперсионного анализа и алгоритмы математической обработки результатов эксперимента изучите самостоятельно [8].

Проведение дисперсионного анализа можно легко осуществить с помощью ПЭВМ с использованием различных общепризнанных статистических программных продуктов: STATGRAPHICS, STADIA [7], STATISTICA и др.

5.2.3. Пример составления плана эксперимента и проведения однофакторного дисперсионного анализа

С целью определения влияния типа катализатора (х) на выход нитробензола (y) при его синтезе из бензола был спланирован и проведен однофакторный (k = 1) четырехуровневый (m = 4) эксперимент с двукратным повторением каждого опыта (n = 2) и получены следующие единичные результаты измерений (табл. 13).

Таблица 13

План и результаты однофакторного эксперимента

Номер повторного	Выход нитробензола (y), мас. %, при использовании катализатора (хv)
опыта i	х1 (без катализатора)	х2 (катализа­тор № 1)	х3 (катализа­тор № 2)	х4 (катали­за­тор № 3)

 

Наличие повторений опытов при эксперименте позволяет применить для обработки его результатов метод однофакторного дисперсионного анализа.

Расчеты однофакторного дисперсионного анализа полученных результатов эксперимента были выполнены на ПЭВМ с помощью пакета прикладных программ "STATISTICA", и их итоги представлены в
табл. 14.

Таблица 14

Итоги расчетов однофакторного дисперсионного анализа

Источник дисперсии	Сумма квадратов	Число степе­ней свобо­ды	Средний квадрат	Fp	Уровень значимо­сти
Фактор х	1750,000		583,3333	38,88889	0,002037
Случайные факторы	60,000		15,0000	-	-

 

Данные табл. 14 показывают, что тип катализатора влияет на выход нитробензола с вероятностью более 0,997 (Р = 1- a = 1-0,002037 = 0,099763).

Применим метод попарного сравнения средних арифметических результатов измерений для определения уровня фактора х, при котором влияние на свойство y превышает ошибки эксперимента.

Алгоритм расчетов зависит от соблюдения равенства выборочных дисперсий единичных значений ( и ).

Первоначально сравним выход нитробензола при реакции без катализатора (v =1) и с катализатором № 2 (v = 3). Выполним расчеты соответствующих параметров:

мас. %; мас. %;

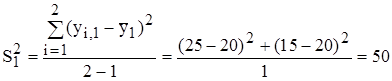(мас. %)²;

(мас. %)².

Проверим равенство (однородность) выборочных дисперсий единичных значений:

;

F_т (Р = 0,95; f₁ = f₂ = n-1 = 2-1 =1) = 164,4;

F_p > F_т (¥ > 164,4).

Таким образом, с вероятностью 0,95 сравниваемые дисперсии и 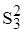не однородны, т.е. не равны (различия между ними "значимы"). Так как одна из дисперсий равна нулю, то воспользуемся T-критерием [8]:

; ; ;

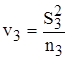(мас. %)²; (мас. %)²;

t_т (Р = 0,95; f = n-1 = 2-1 =1) = 12,71;

мас. %;

< T.

Таким образом, исходя из полученного неравенства с вероятностью 0,95 следует считать, что катализатор № 2 не влияет на выход нитробензола при его синтезе.

Сравнение других пар средних арифметических значений показало, что с вероятностью 0,95 можно утверждать об увеличении выхода нитробензола при введении в реакцию его синтеза и катализатора № 3. Катализатор № 3 имеет более высокую эффективность действия в исследованной реакции по сравнению с катализатором № 2.

Следует иметь в виду, что применение дисперсионного анализа дает более точные выводы, если величины y и x _j имеют нормальное распределение. В противном случае для качественной оценки зависимости j лучше использовать непараметрические методы факторного анализа.

5.3. Планирование эксперимента для применения регрессионного
анализа

5.3.1. Некоторые общие положения регрессионного анализа

Регрессионный анализ (РА) - метод математической статистики, который позволяет выявить приближенную количественную зависимость (f) свойства объекта y от значений факторов x _j, оказывающих влияние на это свойство. Эта приближенная зависимость, выраженная в виде конкретной математической функции, называется уравнением регрессии:

.

Проводить РА можно только для количественных значений y и x _j.

При РА решают две основные задачи:

1. Ищут с помощью метода приближения уравнение регрессии, наиболее точно описывающее истинную зависимость y = j(x _j) по результатам измерения свойств объекта при различных значениях факторов:

y = j(x ₁, x ₂,..., x _j,... x _k) + e = f(x ₁, x ₂,..., x _j,... x _k) + q + e.

2. Оценивают ошибки (q + e), допускаемые при описании истинной зависимости j с помощью найденного уравнения регрессии.

Порядок проведения РА (его тип) зависит от плана эксперимента. Различают классический РА (КРА) и РА при математическом планировании эксперимента (РАМПЭ).

5.3.2. Составление планов эксперимента для проведения регрессионного анализа

5.3.2.1. Составление планов эксперимента для проведения классического регрессионного анализа

Общим требованием к планированию любого эксперимента для проведения КРА является выполнение условия m_j > 2. Другие рекомендации аналогичны планированию эксперимента для проведения дисперсионного анализа.

После планирования и завершения эксперимента проведение КРА его результатов проводят в такой последовательности:

Выбирают семейство математических функций, в котором предполагается найти уравнение регрессии (семейство прямых, парабол, гипербол и др.).

Выбирают метод приближения.

Для выбранного семейства функций с помощью метода приближения рассчитывают параметры функции (коэффициенты уравнения регрессии).

Проверяют рассчитанные коэффициенты уравнения регрессии на значимость (равенство нулю).

Корректируют вид исходной функции, исключая из нее незначимые коэффициенты и другие составляющие.

Рассчитывают параметры скорректированной функции (скоррек­тированные коэффициенты уравнения регрессии) и возвращаются к выполнению пунктов 4,5. Пункт 6 выполняют до тех пор, пока в уравнении регрессии останутся только значимые коэффициенты (значения коэффициентов могут изменяться после каждого пересчета)

Оценивают ошибки (q + e), допускаемые при описании истинной зависимости j с помощью найденного уравнения регрессии: проверяют адекватность уравнения регрессии с помощью закона распределения Фишера или рассчитывают вероятность описания зависимости j функцией f.

Выбирают другое семейство математических функций и (или) метод приближения и с ними последовательно выполняют пункты 3-7.

Из группы найденных уравнений регрессии в ряду разных семейств функций выбирают окончательное уравнение регрессии по следующим соображениям:

а) вид данного уравнения регрессии совпадает с теоретическими законами поведения объекта;

б) данное уравнение регрессии описывает поведение объекта с наибольшей вероятностью;

в) при одной вероятности для данного уравнения регрессии наблюдается наибольшее значение соотношения факторной и остаточной дисперсий (F-соотношения).

При выборе семейства функций (пункты 1 и 8), если нет сведений или теоретических предположений о типе зависимости j, обычно действуют по принципу "от простого к сложному". При этом начинают с семейства прямых ("линейная регрессия") или трансцендентных функций, которые легко преобразуются в линейную форму ("трансцендентная регрессия").

При неадекватности найденного линейного уравнения регрессии или неудовлетворенности его точностью можно переходить к семейству полиномов с постепенным увеличением их степени (полиномы второго, третьего и др. порядков) до тех пор, пока не начнет уменьшаться F-соот­ношение. Вид функции также зависит от числа одновременно изменяемых факторов при эксперименте.

Наиболее часто при выполнении РА в качестве метода приближения используют метод наименьших квадратов (МНК). Однако применение МНК является корректным при выполнении следующих требований:

а) единичные результаты измерения свойств y должны быть независимыми случайными величинами;

б) выборочные дисперсии y _z должны быть однородными (одинаковыми).

При невыполнении этих условий используют другие методы приближения (непараметрические методы регрессии).

Алгоритмы всех необходимых при КРА расчетов (пункты 3,4,6,7) зависят от выбранного семейства функций, метода приближения, наличия повторных опытов, количества исследуемых факторов (изучить самостоятельно [6,7,8,11]). Многие из этих алгоритмов реализованы в статистических программных продуктах, математических пакетах (MathCAD и др.), электронных таблицах (E x cel и др.).

Следует отметить, что выполнение пункта 9 носит субъективный характер и для него пока еще нет общепризнанных рекомендаций.

Пример проведения классического регрессионного анализа. Воспользуемся для примера данными эксперимента, приведенными в
табл. 7.

По полю корреляции (см. рис. 4) можно предположить линейный характер зависимости y от х, поэтому начнем проведение КРА с выбора семейства прямых и представления искомого уравнения регрессии в виде

= а + b x.

Так как в этом эксперименте не проводились повторные опыты, то невозможно оценить однородность дисперсий при различных уровнях фактора х и установить закон распределения y. Поэтому делаем допущение о нормальном законе распределения y и равенстве дисперсий (одинаковой случайной ошибке при любом значении х). Тогда в качестве метода приближения можно взять МНК.

Используя метод МНК и учитывая отсутствие повторных опытов, выполним расчеты коэффициентов уравнения регрессии а и b [1]:

b = 1,3 (мас. %/мин); a = ` y - b` x = 42,5 - 1,3×115;

а = - 107 (мас. %).

 

Так как дисперсия воспроизводимости эксперимента неизвестна и ее невозможно определить (из-за отсутствия повторных опытов), то проверку коэффициентов а и b на значимость не проводим. Делаем допущение, что эти коэффициенты "значимы", т.е. не равны нулю.

Найденное линейное уравнение регрессии имеет следующий вид:

= - 107 + 1,3 х.

Для оценки ошибки, допускаемой при описании истинной зависимости j с помощью найденного уравнения регрессии при отсутствии повторных опытов и дисперсии воспроизводимости, составим F-соотно­шение (F_p) между дисперсией относительно` y () и остаточной дисперсией () в соответствии со следующими формулами:

; ; ,

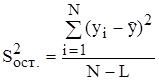где L - число значимых коэффициентов в скорректированном уравнении регрессии (L = 2).

Выполним необходимые расчеты:

,

» 290 (мас. %)²;

,

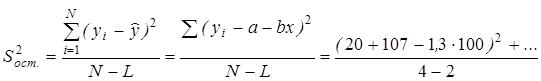15 (мас. %)²;

;

% = 95 %;

(где R - выборочный корреляционный коэффициент Пирсона, R² - коэффициент детерминации).

Найденное линейное уравнение регрессии ( = - 107 + 1,3 х) с вероятностью, большей 0,95, адекватно описывает реальную зависимость выхода нитробензола от времени его синтеза, так как значение соотношения F_p больше табличного значения квантиля распределения Фишера при a=0,05 и степенях свободы f₁ = N-1 и f₂ = N-L (F_т = 19,2). Точность описания (коэффициент детерминации R²) реальной зависимости найденным линейным уравнением регрессии составляет 95 %.

Подобные расчеты были выполнены на ПЭВМ с помощью статистического пакета STATGRAPHICS [7] не только для семейства прямых, но и некоторых других функций (табл. 15).

Данные табл. 15 показывают, что выход нитробензола зависит от времени его синтеза и эта зависимость с наибольшей вероятностью (Р» 0,983) описывается линейным уравнением вида

= - 107 + 1,3 х.

Оба коэффициента уравнения регрессии (а = - 107 и b = 1,3) с вероятностью Р > 0,96 являются "значимыми" (т.е. не равными нулю), так как уровень их значимости равен соответственно a_а = 0,033 и a_b = 0,017.

 

 

Таблица 15

Результаты расчетов на ПЭВМ

Функ­ция	Коэф­фици­ент	F-	Адек-
	обо­з­на­­че­ние	значе­ние	S	tт	a	соот- но-ше- ни­	ват-­ но­сть (a)
y = a + b x	a b	- 107 1,3	20,013 0,173	- 5,347 7,506	0,033 0,017	56,33	0,017
y = e(a+b x)	a b	- 0,3741 0,03519	0,9969 0,0086	-0,375 4,078	0,744 0,055	25,88	0,055
1/ y = a + b x	a b	0,14867 -0,00105	0,0423 0,0004	3,5128 -2,867	0,072 0,103	11,07	0,103

 

Более подробно с проведением классического регрессионного
анализа для практических целей можно ознакомиться в [11].

5.3.2.2. Математическое планирование эксперимента для проведения регрессионного анализа

В современных условиях, учитывая многогранность изучаемых явлений, острый дефицит времени, высокую стоимость эксплуатации научного оборудования, необходимо стремиться к наиболее рациональным планам проведения эксперимента.

Применение методов математического планирования эксперимента для проведения регрессионного анализа (РАМПЭ) приводит к увеличению точности получаемого уравнения регрессии, а иногда и к значительному сокращению числа опытов.

В основу методов математического планирования эксперимента для проведения РА положен принцип "черного ящика". Суть этого принципа заключается в том, что исследователь, не зная об истинных закономерностях поведения объекта, описывает его с помощью статистических математических моделей.

Образно говоря, "ударяя" по исследуемому объекту изменением входных параметров (x _j) в ходе эксперимента (рис. 6) и измеряя его реакцию (y _v) на эти "удары" при действии случайных факторов (w_z), можно получить статистическую математическую зависимость, пригодную для прогноза поведения объекта.

2 Рекомендуемая литература [1].

⇐ Предыдущая1234567

Поделиться:

Воспользуйтесь поиском по сайту: