I. Определение обратной матрицы

Квадратная матрица А называется вырожденной, если ее определитель равен нулю, и невырожденной, если ее определитель не равен нулю.

Если А — квадратная матрица, то обратной по отношению к А называется матрица, которая, будучи умноженной на А (как справа, так и слева), дает единичную матрицу.

Обозначив обратную матрицу через А запишем

Если обратная матрица А существует, то матрица А назы­вается обратимой. Операция вычисления обратной матрицы при условии, что она существует, называется обращением матрица. Нахождение обратной матрицы имеет большое значение при решении систем линейных уравнений и в вычислительных мето­дах линейного программирования.

▲ Теорема. Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. е. чтобы ее определитель был отличен от нуля.

При условии обратная матрица находится по формуле

Вычисление обратных матриц второго и третьего порядков

Для нахождения обратной матрицы используют следующую схему:

1°. Находят определитель матрицы А.

2°. Находят алгебраические дополнения всех элементов а_ij матрицы А и записывают новую матрицу.

3⁰. Меняют местами столбцы полученной матрицы (транспо­нируют матрицу).

4°. Умножают полученную матрицу на 1/D.

52. Найти матрицу, обратную матрице

53. Найти матрицу, обратную матрице

Поскольку , матрица А является невырожденной и, значит можно найти матрицу А^-1.

2°. Найдем алгебраические дополнения всех элементов матри­цы А:

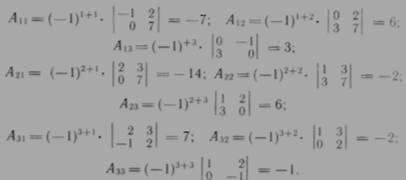
Запишем новую матрицу:

3 . Транспонируем полученную матрицу:

4°. Умножив полученную матрицу на ,находим

Проверим полученный ответ. Имеем

Последовательно находим:

54—59. Найти матрицы, обратные заданной матрице А:

Решение простейших матричных уравнений

• 1. Простейшие матричные уравнения и их решение

• 2. Решение системы линейных уравнений в матричной форме

Простейшие матричные уравнения и их решение

Пусть дана система уравнений

Рассмотрим матрицу, составленную из коэффициентов при неизвестных:

Свободные члены и неизвестные можно записать в виде матриц столбцов:

Тогда, используя правило умножения матриц, эту систему уравнений можно записать так:

Это равенство называется простейшим матричным уравне­нием.

Такое уравнение решается следующим образом. Пусть матри­ца А — невырожденная : тогда существует обратная матрица А^-1. Умножив на нее обе части матричного уравнения, имеем

Используя сочетательный закон умножения, перепишем это ра­венство в виде

Поскольку , находим

Таким образом, чтобы решить матричное уравнение, нужно:

1°. Найти обратную матрицу А^-1

2°. Найти произведение обратной матрицы А^-1 на матрицу-столбец свободных членов В, т. е. А^-1В.

3°. Пользуясь определением равных матриц, записать ответ.

60. Решить матричное уравнение

Решение.1°. Будем искать обратную матрицу А^-1.

Найдем определитель матрицы А:

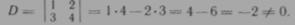
Вычислим алгебраические дополнения каждого элемента матрицы А:

3°. Так как , то по определению равных матриц получим .

61. Решить матричное уравнение

 

и транспонируем ее:

Учитывая, что , запишем обратную матрицу:

2°. Имеем

62—65. Решить матричные уравнения:

Решение системы линейных уравнений в матричной форме

Так как систему линейных уравнений можно записать в виде матричного уравнения, то эту систему можно решить как матрич­ное уравнение.

66. Решить матричным способом систему уравнений

Решение. Составим матричное уравнение , где

и решим его указанным способом. Находим

Итак, решение системы уравнений есть .

67—70. Решить матричным способом системы линейных уравне­ний:

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: