Геометрические величины в школьном курсе математики.

Величина и ее измерение

Го­воря далее о величинах, будем иметь в виду скалярную, аддитив­ную, непрерывную положительную величину.

Интуитивно мы представляем себе, что величина может быть больше или меньше, две однородные величины могут складывать­ся, величину можно делить на любое натуральное число, ее мож­но измерить, причем под измерением обычно понимают сравне­ние данной величины с другой того же рода, принятой за единицу измерения..

Рассмотрим бесконечное множество В с введенным в нем отно­шением < (меньше) и операцией + (сложение), т. е. (В,<,+), которое назовем системой однородных величин (или системой величин, или родом величин). Элементы а,b, с,... или а₁, а₂,... множества В назовем однородными величинами или величинами одного рода.

Система величин (В,<,+) характеризуется следующими свой­ствами, которые могут быть приняты за исходные предложения (аксиомы) теории величин:

1) а, b (а>Ь или а=b или b<а) (причем имеет место только одно из трех соотношений).

2) а, b, с (а<b и b<с =>а<с) (транзитивность отношения «мень­ше», а также «больше», которое может быть определено через «меньше», а>b 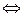b<а).

3) а, b ! с (а+b=с) (замкнутость В относительно сложения).

4) а, b (а+b=b+а) (коммутативность сложения).

5) а, b, с (а+(b+с)=(а+b)+с) (ассоциативность сложения).

6) а, b (а+b>а) (монотонность сложения).

7) а, b а>b => !с (b+с=а)) (возможность вычитания а-b=с),

8) а, n N b (nb=а) (возможность деления величины на на­туральное число: а:n=b).

9) а, b n N (а<nb) (аксиома Архимеда).

10) пусть даны две последовательности величин из В: а₁<а₂<...<...; ...<...<b₂<b₁ причем для любой величины с при доста­точно большом номере п b_n-а_n<с, т. е. члены последовательностей (а_п) и (b_п) неограниченно приближаются друг к другу. В таком слу­чае существует единственная величина хеВ, которая больше всех а_n и меньше всех b_n т. е.

с nеN (b_n -а_n <с)=> ! х В n N (а_n <х<b_n) (аксиома непрерывности).

Свойства 1-10 полностью определяют понятие системы поло­жительных скалярных величин.

Если какую-нибудь величину е В принять за единицу измере­ния» то всякая величина системы В однозначно представлена в виде а= 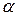е_, где 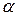- положительное действительное число (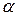 R⁺) - мера величины а при единице измерения е. Меру 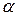при единице изме­рения е обозначим через m(а), т. е. если а = 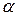е, то 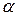= m(а).

Мера обладает следующими свойствами:

а) m - функция в области определения В и области значения R⁺, т.е. т отображает В на R⁺;

б) а<b=>m(a)<m(b) (монотонность меры);

в) m(а+b)=m(а)+m(b) (аддитивность меры);

г) m(е)=1 (мера единицы измерения равна 1).

Перечисленные свойства полностью характеризуют меру т. Су­ществует единственная функция

В 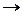R⁺, обладающая этими свой­ствами, а именно мера m(а) величины 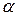при единице измерения е. Если заменить е на е ', то получится новая мера m'(а)= 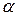', причем, т.к. m'(а)= 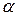, связь между двумя мерами выразится так: m'(а)= 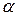^-1m(а).Перечисленные свойства общего понятия величины и меры величи­ны находят применение (в явном или неявном виде) при изучении кон­кретных геометрических величин (длины, площади и объема) в школе.

Методические особенности изучения геометрических величин.

Измерение геометрических величин изучается в школьном курсе дважды, на двух различных уровнях.

На первом, чисто экспериментальном, уровне в начальных классах учатся измерять длины отрезков, площади простейших плос­ких фигур и объемы простейших пространственных тел. На этом уровне не дается определений длины, площади и объема.

Цель состоит в том, чтобы создать у учащихся ясные интуи­тивные понятия.

Рассмотрим некоторые вопросы методики изучения геометри­ческих величин на втором уровне.

Можно ли строго эту теорию построить в школьном курсе? Раз­ные точки зрения, много трудностей, много логических пробелов.

Например, в учебнике АЛ. Киселева площадью называется «величина части плоскости, заключенной внутри многоугольника или какой-нибудь другой плоской замкнутой фигуры», далее мы читаем: «Площадь прямоугольника равна произведению его осно­вания на высоту». Далее, правда, есть разъяснение, что это крат­кая формулировка и надо понимать «число, выражающее площадь прямоугольника в квадратных единицах и т. д.». В сознании уча­щихся остается только первая формулировка.

Аналогично у А.П. Киселева обстоит дело и с определением понятия объема. Объем определяется как величина части про­странства, занимаемой геометрическим телом, а дальше - теоре­ма V=аЬс (V - объем прямоугольного параллелепипеда).

Наряду с этим обращает на себя внимание тот разнобой, который имеет место при отыскании числа, выражающего объемы различных тел.

Именно поэтому «школьная теория» измерения геометрических величин должна строиться таким образом, чтобы четко вырисовывалась общая схема. Это относится к определениям понятий «дли­на», «площадь», «объем». Раскрытие связей по общей схеме спо­собствует более глубокому пониманию и прочности знаний.

Каждое из трех понятий определяется как вещественное чис­ло, удовлетворяющее условиям (а - г), которые характеризуют об­щее понятие меры множества.

Можно наметить следующую схему теории измерения длин отрезков:

1) определение длины отрезка как вещественного числа, удов­летворяющего условиям (свойствам меры а - г);

2) описание процедуры измерения отрезков;

3) установление существования и единственности длины отрез­ка при данном выборе единицы измерения с использованием ак­сиомы Архимеда;

4) установление существования отрезка, длина которого при данном выборе единицы измерения равна любому, наперед задан­ному положительному числу с использованием аксиомы Кантора» геометрического эквивалента аксиомы непрерывности (11).

Разъяснение учащимся старших классов сущности аксиомы Кантора (обычно не рассматривается в школьном курсе) не пред­ставляет особых трудностей. Это можно сделать именно в связи с установлением свойства 4.

Случай, когда наперед заданное число - рациональное, не тре­бует применения аксиомы Кантора и выполняется с помощью эле­ментарного построения.

Но вот когда число иррациональное (например, х=2,31311311131111...), то при разъяснении приходим к аксиоме Кан­тора;

«Если на прямой дана бесконечная последовательность отрез­ков А₁В₂, А₂,В₂,..., А_nВ_n,... такая, что, во-первых, каждый отрезок лежит внутри предыдущего; во-вторых, нет отрезка, лежащего внутри всех отрезков этой последовательности, то существует точ­ка, лежащая внутри всех отрезков этой последовательности». Един­ственность этой точки непосредственно следует из аксиомы. И таким образом, строим отрезок х.

Теория измерения площадей и объемов в некоторой части аналогичны. Подчеркивание этой аналогии в процессе обучения -эффективное средство формирования понятия о методике постро­ения этих теорий.

Аналогия заключается в выборе единицы измерения (квадрат со стороной 1 - куб с ребром 1), а также в последовательности и е доказательств предложении.

Однако это не распространяется на всю теорию. Например, нельзя проводить аналогию в вопросах о равновеликости и равно­составленности площадей и объемов, хотя определения этих поня­тий вводятся аналогично. Но, если всякие равновеликие многоуголь­ники равносоставлены, то этого нельзя сказать о равновеликих мно­гоугольниках:«Два многоугольника (многогранника), которые можно разло­жить на одинаковое число попарно конгруэнтных многоугольни­ков (многогранников), называются равносоставленными ».

Практическое занятие №12

Тема Изучение вопросов взаимного расположения прямых и плоскостей в пространстве.

Содержание практического занятия:

1. Первые уроки стереометрии

2. Взаимное расположение прямых в пространстве

3. Взаимное расположение плоскостей в пространстве

Литература: [1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II, III, IV. Учебники геометрии 10-11 класса.

Первая встреча с параллельными прямыми происходит в 6 классе. Это обусловлено в целях пропедевтики и рассмотрения координатной плоскости. Созданию образа || прямых служат наблюдения окружающей обстановки. Важное значение имеют: формирование практических умений построения || прямых с использование м линейки и угольника. Учащиеся знакомятся с признаком параллельности прямых. Вопрос о взаимном расположении прямых изучается одним из прямых в курсе планиметрии (7 класс), а поэтому требует особого внимания к разработке их содержания и методики их преподавания, уже при изучении этих разделов целесообразно в доступной форме раскрывать роль основных свойств (аксиом). Создавать первые представления об аксиомах как о рабочем инструменте. Большая роль отводится аксиоме «через любые две точки можно провести прямую и только одну». Учение о параллельности в курсе планиметрии можно разделить на следующие части: определение || прямых, существование || прямых, построение || прямых, аксиома || прямых, свойства ||, признаки || - ти, применение изученной теории в решении задач. Последний раздел присутствует во всех предыдущих. В 8 классе изучается теорема Фалеса и на ее основе свойства средней линии треугольника и трапеции. Параллельность прямых в пространстве. Основная цель – дать учащимся математические знания о ||-тти Е1 и Е2 в Е3. в теме продолжается знакомство со взаимным расположение Е1 и Е2 в Е3. Рассматривается ||-ть прямых, Е1 и Е2, 2х Е2. Для всех этих случаев даются соответствующие определения и признаки, обсуждаются вопросы существования иединственности. Теоремы сущ-ия доказ-ся конструктивно, что дает учащимся конкретный способ построения Е1 или Е2. Позднее учащиеся знакомятся с одним признаком параллельности плоскостей «Две Е2 ||, если они имеют общий перпендикуляр». В теме обобщаются известные из планиметрии сведения о параллельных прямых. На примере теоремы о существовании и ед-ти прямой || данной Е1, учащиеся получают представления о необходимости заново доказывать известные им из планиметрии факты в тех случаях, если речь идет о точках и прямых Е3, а не конкретной плоскости. Задачи на доказательство решаются во многих случаях конструктивно. В связи с появлением задач на вычисление длины отрезка возникает необходимость целенаправленного повторения планиметрического материала: оперд, свойств признаков параллелограмма, равенство и подобие треугольников и т.д. При решении задач учащиеся должны использовать их в качестве аргумента при обосновании определения признаков параллельности. Теорема о пресечении двух || Е2 третьей Е2 и о пересечении 2х || Е2 2я ||Е1.Темы играют важную роль в процессе формирования пространственных представлений учащихся. Изучение теоретического материала сочетается с решением задач на построение с использованием моделей и рисунков. В теме рассматривается пункт «Изображение пространственных фигур на плоскости». При изучении параллельности в пространстве возникает ряд методических вопросов без решения которых нельзя добиться хороших результатов наиболее важным их них является набор упражнений по теме. Здесь много теорем и следствий из них. Без выполнения упражнений не будет достигнута главная цель, развитие пространственного воображения. Часть упражнений имеет форму вопросов и ставит своей целью уточнение. Правильно. Правильно – ли учащиеся понимают упражнения, аксиомы. Группа один (№2 стр.237). при всей простоте эти упражнения вызывают интерес у учащихся, требуют для получения ответа выполнения схематических рисунков, привлечения моделей. Важно при решении.тих упражнений добиться обоснования ответов. Группа 2 связана с рассмотрением || Е1 и Е2 на готовых чертежах.. Группа 3: задачи на вычисление При решении таких задач используются признаки подобия треугольников, теорема Фалеса, свойства средней линии треуг., трапеции. Группа 4 задачи на доказательство. Группа 5 задачи на построение (воображаемое на проекционном чертеже). Различие этих задач подчеркивается словами «провести» - доказать существование, «построить» - обосновать на чертеже (– воображаемое, – проекционный чертеж).

-Методика изучения перпендикулярности (пер) на Е2 и Е3. Учение о пер-х прямых начинается в 6 классе на интуитивной основе. Изучение пер прям идет в одном классе с || Е1 и взаимосвязаны. В своей основе пер Е1 имеет понятие «угол между Е1». Величиной наименьшего из углов образованного двумя пересекающимися прямыми считают углом между ними. То есть угол между пересекающимися Е1 не может превосходить 90 градусов. В случае, когда угол равен 90 градусов прямые называются пер. Существование пер Е1 показываются конструктивно, даются понятия: серединный пер и наклонная. Методика перпендикулярности в Е3. Основная цель: дать учащимся систему сведений о пер Е1 и Е2 в Е3. Продолжается изучение взаимного расположения Е1и Е2 в Е3. Рассматривается пер прямых, Е1 и Е2, 2х Е2. Материал темы обобщает и систематизирует сведения о пер Е1. При изучении темы возрастает роль задач на вычисление, широко используется теорема Пифагора, теорема о 3х пер, теорема о пер плоскостях. Темой является пропедевтической для изучения многогранников. При решении многих задач, связанных с вычислением длин пер и наклонных е2. речь идет о вычислении элементарных пирамид. Доказывается теорема выражающая признак пер Е1 и Е2. Из изучаемых свойств содержательными являются теорема выражающая зависимости между ||-ью и пер-ью прямых и плоскостей. Теорема: если Е2 пер одной из 2х || Е1, то она пер и другой. Теор. – две Е1 прямые пер одной и той же Е2, то они ||. Во многих учебниках предлагается начинать систематизированный курс стереом - ии с темы «Пер в Е3». В качестве основного аргумента в пользу расположения материала выдвигается возможность решения многих задач ан вычисление начиная с первых уроков геометрии. Сторонники противоположной т.з. отмечают, что задачи на вычисление с успехом могут быть заманены док –ом. В то время как изложение теор-го материала в случае раннего изучения ||-ти выглядит более доступным и имеет ряд преимуществ. Также введение в программу таких вопросов, как ||-ое проектирование, изображение фигур требует знания ряда фактов раздела параллельности. Таким образом принятый порядок изучения в школе: параллельности, затем пер-ти является целесообразным.

Практическое занятие №13

Тема: Изучение темы «Многоугольники» в ШКМ

Содержание практического занятия:

1. Цели изучения темы «Многоугольники»

2. Методика изучения темы «многоугольники» в курсе геометрии 9 класса.

Литература:[1-4],[7],[11-16],[18]. Дополнительная литература I [1-4], II, III, IV. Учебники геометрии 7-9 класса.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: