Метрические характеристики графа.

Расстояние в графах

 

Пусть G= (X,V) – связный неорграф, x_i, x_j – две его несовпадающие вершины. Длина кратчайшего (x_i, x_j) – маршрута называется расстоянием между вершинами x_i, и x_j и обозначается через р (x_i, x_j). Положим р (x_i, x_i) = 0. Очевидно, что введенное таким образом расстояние удовлетворяет следующим аксиомам метрики:

p(x_i, x_j) ³0;

р(x_i, x_i) = 0 тогда и только тогда, когда x_i,=x_j;

p(x_j,x_i,) = p(x_i, x_j) (симметричность):

p(x_i, x_j)£p(x_i, x_k)+p(x_k, x_j) (неравенство треугольника).

Если X={x₁,x₂, …, x_n}, то матрица Р=(p_ij), в которой p_ij=p(x_i,x_j), называется матрицей расстояний. Заметим, что Р^T=Р, т. е. матрица Р симметрична.

Для фиксированной вершины x_i, величина е(x_i)= =max{p(x_i, x_j) | x_jÎ X} называется эксцентриситетом вершины x_i. Таким образом, эксцентриситет вершины равен расстоянию от данной вершины до наиболее удаленной от нее. Если Р – матрица расстояний, то эксцентриситет е (x_i) равен наибольшему из чисел, стоящих в i -й строке.

Максимальный среди всех эксцентриситетов вершин назы­вается диаметром графа G и обозначается через d(G): d(G)=max{e(x_i) | x_i Î X}. Вершина x_i называется периферийной, если e(x_i)=d(G).

Пример. Найдем диаметр графа G, изображенного на рис. 4.21. Матрица расстояний Р имеет вид

 

 

отсюда е(1)=3, е(2)=2, е(3)=3, е(4)=2, е(5)=2 и, следовательно, d(G)=3. Вершины 1 и 3 являются периферийными.

Минимальный из эксцентриситетов графа G называется его радиусом и обозначается через r(G): r(G) = min{e(x_i) | x_i Î М}. Вершина x_i называется центральной, если е(x_i)=r(G). Множество всех центральных вершин графа называется его центром.

Примеры.

1. Радиус графа, показанного на рис. 4.21, равен 2, а его центром является множество {2,4,5}.

2. В полном графе К_п все различные вершины смежны, и поэтому d(K_n) = r(К_n) = 1.

Задача нахождения центральных вершин возникает в практической деятельности людей. Пусть, например, граф представляет собой сеть дорог, т. е. вершины соответствуют населенным пунктам, а ребра – дорогам между ними. Требуется оптимально разместить больницы, пункты обслуживания и т. п. В подобных ситуациях оптимизация заключается в минимизации расстояния от места обслуживания до наиболее удаленного населенного пункта. Следовательно, местами размещения должны быть центральные вершины графа. Реальные задачи отличаются от этой идеальной тем, что приходится учитывать и другие обстоятельства – расстояния между населенными пунктами, стоимость, время проезда и т. д. Для учета этих параметров используются взвешенные графы [4].

Пусть G = (X,V) –взвешенный граф, в котором вес каждой дуги (x_i,x_j) есть некоторое вещественное число m(x_i,x_j). Весом маршрута x₁, x₂,..., x_n, x_n+1, называется число . Взвешенным расстоянием ( - расстаянием) p_v(x_i,x_j) между вершинами x_i и x_j называется минимальный из весов (x_i,x_j)- маршрутов. (x_i,x_j) -маршрут, вес которого равен расстоянию p_v(x_i,x_j), называется кратчайшим (x_i,x_j) -маршрутом в взвешенном графе G. Взвешенным эксцентриситетом e_v (x_i) вершины x_i называется число mах{ p_v(x_i,x_j) | x_j Î М}. Взвешенной центральной вершиной графа G называется вершина x_i, для которой е_v(x_i)=min{е_v(x_j) | x_jÎ М}. Взвешенный эксцентриситет центральной вершины называется взвешенным радиусом графа G и обозначается через r_v(G).

 

4.7. Графы с заданной последовательностью степеней

 

Степенной последовательностью графа называется список степеней его вершин. Часто по степеням вершин графа можно судить о его строении. Естественно возникают следующие вопросы. Как связать между собой степени вершин графа? Как по списку степеней графа судить о его строении? Какова связь между графами с совпадающими списками степеней вершин? Можно ли построить граф с заданным списком степеней вершин и предписанными теоретико-графовыми свойствами и как это сделать?

Последовательность неотрицательных целых чисел называется графической, если существует граф с такими вершинами 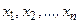, что вершина имеет степень . Этот граф называется реализацией последовательности .

Последовательность обозначается одной буквой D, т. е. D = . Очевидно, что порядок членов в графической последовательности несуществен, а каждый ее член удовлетворяет неравенствам . Часто удобно эти последовательности считать невозрастающими. Согласно лемме о рукопожатиях сумма всех членов графической последовательности является четным числом.

Назовем последовательность правильной, если выполняются два следующих условия:

1) , (4.1)

2) – четное число. (4.2)

 

Без ограничения общности графическую последовательность можно считать правильной.

В общем случае графическая последовательность имеет много реализаций и их число определить сложно. Иногда, хотя и редко граф определяется своей степенной последовательностью однозначно. Если все реализации графической последовательности изоморфны, то эта последовательность называется униграфической, а граф – униграфом.

Рассмотрим последовательность D =(2, 2, 2, 2, 1, 1, 1, 1). Существует ровно пять графов, являющихся реализациями последовательности D. Они имеют следующие компоненты: 1) С ₄, К ₂ и К ₂, 2) К ₃, Р ₃ и К ₂, 3) Р₆ и К ₂, 4) Р ₅ и Р ₃, 5) Р ₄ и Р ₄. Здесь С ₄ – простой цикл, содержащий 4 вершины, Р_n – простые цепи, содержащие n вершин (n =3,4,5,6).

Обоснуем алгоритм построения простого графа (если он существует), имеющего заданную последовательность степеней.

Рассмотрим графическую последовательность 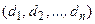, упорядоченную по невозрастанию: . Пусть – степень вершины . «Изъять » означает соединить соответствующую вершину с вершинами , если 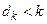, или с вершинами , если . Последовательность , если , или , если , называется остаточной последовательностью после изъятия или просто остаточной последовательностью.

Хакими и Гавел предложили алгоритм построения простого графа (если он существует), имеющего заданную последовательность степеней [3]. Этот результат основан на результате, являющимся частным случаем (при k =1) следующей теоремы.

Теорема 4.7.1. Если последовательность , , является последовательностью степеней простого графа, то этим свойством обладает и остаточная последовательность после изъятия .

Следующая последовательность шагов описывает алгоритм построения простого графа с заданной последовательностью степеней, если он существует.

 

Шаг 1. – последовательность степеней, упорядоченная по невозрастанию. Выберем произвольное ¹0 и «изымем» из последовательности, соединяя вершину с первыми вершинами, не считая саму вершину .

Шаг 2. Упорядочим остаточную последовательность в порядке невозрастания.

Шаг 3. Шаги 1–2 выполнять до тех пор, пока не возникнет одна из следующих ситуаций:

а) все остаточные степени равны 0. В этом случае последовательность степеней является графической. Искомый граф получается в результате выполнения шагов, соответствующих порядку изъятия степеней;

б) хотя бы одна из остаточных степеней отрицательна – это означает, что последовательность не является графической, т. е. не существует простого графа, который ее реализует.

Для иллюстрации описанного алгоритма рассмотрим пример последовательности

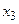
D =(4, 3, 3, 2, 2).

После изъятия 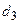(обведенной кружком), получим последовательность

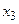
D '=(3, 2, 0, 1, 2),

которая после переупорядочивания остаточных степеней принимает вид

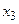
D ₁=(3, 2, 2, 1, 0).

Затем, изымая степень, соответствующую вершине , получим

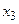
D '₁=(2, 1, 0, 1, 0).

Переупорядочивая остаточные степени в D'₁, получим

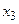
D ₂=(2, 1, 1, 0, 0).

Теперь, изымая степень, соответствующую вершине , получим

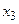
D '₂=(0, 0, 0, 0, 0).

Здесь алгоритм заканчивает работу, так как все остаточные степени равны нулю. Последовательность (4, 3, 3, 2, 2) графическая. Требуемый граф (рис. 4.22) получается в результате выполнения шагов, соответствующих порядку изъятия степеней:

1. Соединяем вершину 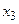с вершинами , и .

2. Соединяем вершину с вершинами и .

3. Соединяем вершину с вершинами и .

 

 

Рис. 4.22. Граф с последовательностью степеней (4, 3, 3, 2, 2)

Замечание. Можно привести пример последовательности, например, (3, 3, 1, 1), для которой условия (4.1) – (4.2) выполняются, но она не является графической. Условия (4.1) – (4.2) не являются достаточными для того, чтобы последовательность была графической.

Достижимость и связность

Основные определения

 

Понятия связности и достижимости используются для исследования структур различных организаций. Например, систему связи любой организации можно интерпретировать как граф, в котором люди представлены вершинами, а каналы связи – дугами. Естественно при рассмотрении такой системы поставить вопрос, может ли информация от одного лица x_i быть передана другому лицу х_j, т. е. существует ли путь, идущий от вершины x_i к вершине х_j. Если в графе существует путь, идущий от вершины x_i к вершине х_j, то говорят, что вершина x_jдостижима из вершины х_i.

Если для любой пары вершин неориентированного графа существует цепь их соединяющая, то такой граф называется связным. Иначе неориентированный граф называется несвязным.

Ориентированный граф называется сильно связным или сильным, если для любых двух различных вершин x_i и x_j существует по крайней мере один путь, соединяющий x_i с x_j. Это определение означает также, что любые две вершины такого графа взаимно достижимы.

Ориентированный граф называется односторонне связным или односторонним, если для любых двух различных вершин x_i и x_j существует по крайней мере один путь из x_i в x_j или из x_j в x_i (или оба одновременно).

Ориентированный граф называют слабо связным или слабым, если для любых двух различных вершин графа существует по крайней мере один маршрут, соединяющий их.

Если для некоторой пары вершин орграфа не существует маршрута, соединяющего их, то такой орграф называется несвязным.

Маршрут есть неориентированный двойник пути. Маршрут позволяет осуществлять «движение» по дугам, без учета их направленности.

Пример. Граф, приведенный на рис. 4.23(а) является сильно связный. Граф, показанный на рис. 4.23(б), не является сильным, так как в нем нет пути из x ₅ в x₂, но односторонне связный. Граф, изображенный на рис. 4.23(в), не является ни сильным, ни односторонним, поскольку в нем не существует путей от x ₅ к x ₂ и от x ₂ к x ₅. Он – слабо связный. Наконец, граф, приведен­ный на рис. 4.23(г), является несвязным.

 

Рис. 4.23. Сильно связный граф (а), односторонне связный граф (б), слабо связный граф (в), несвязный граф (г)

 

Пусть дано некоторое свойство Р, которым могут обладать графы. Максимальным подграфом графа G относительно свойства Р называется порожденный подграф (X_S) графа G, обладающий этим свойством и такой, что не существует другого порожденного подграфа (Х_H), у которого X_S Ì X_H и который также обладает свойством Р. Так, например, если в качестве свойства Р взята сильная связность, то максимальным сильным подграфом графа G является сильный подграф, который не содержится в любом другом сильном подграфе, такой подграф называется сильной компонентой графа G. Это определения можно дать так: всякий максимальный по включению сильно связный подграф данного графа называется его сильной компонентой связности. Аналогично, односторонняя компонента представляет собой односторонний максимальный подграф, а слабая компонента - максимальный слабый подграф.

Например, в графе G, приведенном на рис. 4.23(6), подграф ({ х ₁, x ₄, х ₅, х₆}) является сильной компонентой графа G. С другой стороны, подграфы ({ х ₁, х ₆}) и ({ х ₁, х ₅, х ₆}) не являются сильными компонентами, хотя и являются сильными подграфами, поскольку они содержатся в графе ({ х ₁, x ₄, x ₅, х ₆}) и, следова­тельно, не максимальные. В графе, показанном на рис. 4.23(в), подграф ({ x ₁, x ₄, х ₅}) является односторонней компонентой. В графе, приведенном на рис. 4.23(г), оба подграфа ({ х ₁, х ₅, х ₆}) и ({ х ₂, х ₃, x ₄}) являются слабыми компонентами, и у этого графа только две такие компоненты.

Из определений сразу же следует, что односторонние компоненты графа могут иметь общие вершины. Сильная компонента должна содержаться по крайней мере в одной односторонней компоненте, а односторонняя компонента содержится в некоторой слабой компоненте данного графа G.

Максимальный связный подграф неориентированного графа G называется компонентой связности.

Максимальный сильно связный подграф ориентированного графа G называется сильной компонентой связности (СК).

Существуют два вида связности – вершинная связность и реберная связность. Число вершинной связности – это наименьшее число вершин, удаление которых (вместе с инцидентными ребрами) приводит к несвязному графу. Число реберной связности – это наименьшее число ребер, удаление которых приводит к несвязному графу. При исследовании коммуникационных и логических сетей числа связности соответствующих графов можно интерпретировать как степень надежности этих сетей.

 

 

Матрицы достижимостей

И контрдостижимостей

 

Матрица достижимостей графа G =(X, V) , определяется следующим образом:

 

Множество вершин R (x _i) графа G, достижимых из заданной вершины x_i, состоит из таких элементов x_j, для которых (i, j)-й элемент в матрице достижимостей равен 1. Считают, что каждая вершина достижима из себя самой с помощью пути длины 0, поэтому все диагональные элементы в матрице R равны 1.

Поскольку Г(x_i) является множеством таких вершин x_j, которые достижимы из x_i c использованием путей длины 1 (т.е. Г(x_i) – такое множество вершин, для которых в графе суще­ствуют дуги (x_i, x_j)) и поскольку Г(x_j) является множеством вершин, достижимых из x_j с помощью путей длины 1, то множество Г(Г(x_i))=Г²(x_i) состоит из вершин, достижимых из x_i c использованием путей длины 2. Аналогично Г^p(x_i) является множеством вершин, которые достижимы из x_i с помощью путей длины р.

Так как любая вершина графа G, которая достижима из x_i, должна быть достижима с использованием пути (или путей) дли­ны 0, или 1, или 2,..., или р (с некоторым конечным р≤n), то множество вершин, достижимых из x_i, можно представить в виде

R (x_i) = { x_i }ÈГ(x_i)È Г² (x_i)È…È Г^p (x_i) (4.3)

Таким образом, множество R (x_i) может быть получено последова­тельным выполнением (слева направо) операций объединения в соотношении (4.3), до тех пор, пока «текущее» множество не перестанет изменяться при очередной операции объединения. С этого момента последующие операции не будут давать новых элементов множеству и, таким образом, будет получено, достижимое множество R (x_i). Число объединений, которое нужно выполнить, зависит от графа, но, очевидно, что число р меньше числа вершин в графе.

Матрицу достижимостей можно построить так. Находим достижимые множества R (x_i) для всех вершин x_i Î Х способом, приведенным выше. Положим r_ij =1, если x_j Î R (x_i), и r_ij =0 в противном случае. Полученная таким образом матрица R является матрицей достижимостей.

Матрица контрдостижимостей (матрица обратных достижимостей) , определяется следующим образом:

 

Контрдостижимым множеством Q (x_i) графа G является множество таких вершин, что из любой вершины этого множества можно достигнуть вершину x_i. Аналогично построению достижимого множества R (x_i) на основе соотношения (4.3) можно «сформиро­вать» множество Q (x_i), используя следующее выражение:

Q (x_i) = { x_i } È Г^-1 (x_i) È Г^-2 (x_i) È … È Г^-р (x_i), (4.4) где Г^-2 (x_i) = Г^-1 (Г^-1 (x_i)) и т. д.

Операции, выполняются слева направо до тех пор, пока очередная операция объединения не перестанет изменять «текущее» множе­ство Q (x_i).

Из определений очевидно, что столбец x _i матрицы Q (в котором q_ij= 1, если x_i Î Q (x _i), и q_ij =0 в противном случае) совпадает со строкой x _i матрицы R, т. е. Q = R ^T, где R ^T – матрица, транспонированная к матрице достижимостей R.

Пример. Найти матрицы достижимостей и обратных достижимостей для графа G, приведенного на рис. 4.24.

 

Рис.4.24

Матрица смежности графа G имеет вид

 

 

Множества достижимостей находятся с помощью соотношений

R (x ₁)={ x ₁} È { x ₂, x ₅} È { x ₂, x ₄, x ₅} È { x ₂, x ₄, x ₅} = { x ₁, x ₂, x ₄, x ₅},

R (x ₂)= { x ₂} È { x ₂, x ₄} È { x ₂, x ₄, x ₅} È { x ₂, x ₄, x ₅} = { x ₂, x ₄, x ₅},

R (х ₃)= { x ₃} È { x ₄} È { x ₅} È { x ₅} = { x ₃, x ₄,x₅},

R (х ₄)= { x ₄} È { x ₅} È { x ₅} = { x ₄, x ₅},

R (х ₅)= { x ₅} È { x ₅} = { x ₅},

R (х ₆)= { x ₆} È { x ₃, x ₇} È { x ₄È x ₆} È { x ₃, x ₅, x ₇} È { x ₄, x ₅, x ₆}=

= { x ₃, x ₄, x ₅, x ₆, x ₇},

R (х ₇)= { x ₇} È { x ₄, x ₆} È { x ₃, x ₅, x ₇} È { x ₄, x ₅, x ₆}=

= { x ₃, x ₄, x ₅, x ₆, x ₇}.

Следовательно, матрица достижимостей имеет вид

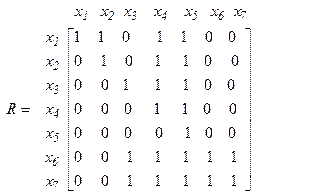матрица обратных достижимостей такова:

 

Так как R (x_i) является множеством вершин, достижимых из x_i, а Q (x_j)– множеством вершин, из которых можно достиг­нуть x_j, то – множество таких вершин, каждая из которых принадлежит по крайней мере одному пути, идущему от x_i к x_j. Эти вершины называются существенными или неотъем­лемыми относительно двух концевых вершин x_i и x_j. Все остальные вершины называются несуществен­ными или избыточными, поскольку их удаление не влияет на пути от x_i к x_{j .}

Матрицы достижимостей и обратных достижимостей являются полными в том смысле, что на длины путей от x_i к x_j не накладывались никакие ограничения. С другой стороны, можно определить матрицы ограниченных достижимостей и контрдостижимостей – надо потребовать, чтобы длины путей не превышали некоторого заданного числа. Эти ограниченные матрицы тоже могут быть построены с помощью соотношений (4.3) и (4.4) – надо действовать точно так, как раньше, при нахожде­нии «неограниченных» матриц, но только теперь р будет верхней границей длины допустимых путей.

Для неориентированного графа множество достижимости позволяет проверить граф на связность. Опишем алгоритм проверки связности неорграфа.

Шаг 1. G =(X, V) – данный неорграф. Для произвольной вершины х_i Î Х найти множество R (x_i). Перейти к шагу 2.

Шаг 2. Если R (x_i)= X, то граф является связным, иначе граф не является связным. Выдать соответствующее сообщение. Останов.

 

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: