Главная | Обратная связь | Поможем написать вашу работу!
 МегаЛекции

Независимые и доминирующие множества




 

Число доминирования, число независимости, кликовое число - эти числа и связанные с ними подмножества вершин описывают важные структурные свойства графа и имеют разнообразные непосредственные приложения при ведении проектного планирования исследовательских работ, в кластерном анализе, параллельных вычислениях на ЭВМ, при размещении предприятий обслуживания, а также источников и потребителей в энергосистемах. Ядро - множество вершин, которое является одновременно минимальным доминирующим и максимальным независимым, имеет важное значение в теории игр.

Множество вершин называется независимым (внутренне устойчивым множеством), если никакие две из них не смежны. Например, для графа, изображенного на рис. 4.27, независимыми являются множества вершин: { x 7, x 8, x 2}, { x 3, x 1}, { x 7, x 8, x 2, x 5}. Когда не могут возникнуть недоразумения, эти множества будут называться просто независимыми множествами (вместо независимые множества вершин).

 

Рис. 4.27

 

Независимое множество называется максимальным, если нет другого независимого множества, в которое оно бы входило. Для графа, изображенного на рис. 4.27, множество { x 7, x 8, x 2, x 5} является максимальным, а { x 7, x 8, x 2} таковым не является. Следует отметить, что число элементов (вершин) в разных максимальных множествах, как следует из приведенного примера, не обязательно одинаковое.

Если Q является семейством всех максимальных независимых множеств G, то число

называется числом независимости графа G, а множество S *, на котором этот максимум достигается, называется наибольшим независимым множеством. Для графа на рис. 4.27 семейство максимальных независимых множеств таково: { x 7, x 8, x 2, x 5}, { x 1, x 3, x 7}, { x 2, x 4, x 8}, { x 6, x 4}, { x 6, x 3},{ x 1, x 5, x 7}, { x 1, x 4}, { x 3, x 7, x 8}.

Наибольшее из них множество имеет 4 элемента и, следовательно, . Множество { x 7, x 8, x 2, x 5} является наибольшим независимым множеством.

Пример. Пусть имеется n проектов, которые должны быть выполнены. Допустим, что для выполнения проекта xi требуется некоторое подмножество Ri наличных ресурсов из множества{1, 2, …, p }. Предположим, что каждый проект, задаваемый совокупностью средств, необходимых для его реализации, может быть выполнен за один и тот же промежуток времени. Построим граф G, каждая вершина которого соответствует некоторому проекту, а ребро (xi, xj) – наличию общих средств у проектов xi и xj, т. е. условию . Максимальное независимое множество вершин графа G представляет тогда максимальное множество проектов, которое можно выполнить одновременно за один и тот же промежуток времени.

Реальная ситуация соответствует динамической системе, в которой происходит постоянное обновление проектов через определенный промежуток времени. Поэтому каждый раз надо заново повторять процедуру построения максимального независимого множества в соответствующем графа G. В практических ситуациях бывает весьма не просто выполнить множество проектов, соответствующих максимальному независимому множеству на данном отрезке времени, поскольку исполнение некоторых проектов может быть по каким-то причинам отложено. Тогда лучший способ действия состоит в присвоении каждому проекту (вершине) xi некоторого штрафа рi, который увеличивается с ростом времени отсрочки в исполнении проекта. В каждый расчетный момент времени надо выбирать из семейства максимальных независимых множеств такое множество, которое максимизирует некоторую функцию штрафа на вершинах, содержащихся в выбранном множестве.

Множество ребер называется независимым, если никакие два из них не смежны. Наибольшее число ребер в независимом множестве ребер называется реберным числом независимости и обозначается β 1. Для полного графа с четным числом вершин β 1(К2n)= n, для полного графа с нечетным числом вершин β 1(К2n +1)= n –1. Независимое множество ребер называется также паросочетанием.

Независимость тесно связана с понятием доминирования.

Для графа G =(X, V) множество вершин D ⊆ Х называется доминирующим множеством (внешне устойчивым множеством), если , то есть для каждой вершины x j∉ D существует дуга, идущая из некоторой вершины xi ∈ D в xj.

Доминирующее множество называется минимальным, если его подмножество не является доминирующим. Как и в случае максимальных независимых множеств, в графе может быть несколько минимальных доминирующих множеств, и они не обязательно содержат одинаковое число вершин. Доминирующее множество называется наименьшим, если число элементов в нем минимально. К задачам такого типа относят, например, следующие:

1) Размещение телевизионных или радиопередающих станций на некоторой территории.

2) Размещение центров торговли обслуживающих некоторые районы.

Теорема 4.9.1. Независимое множество вершин является максимальным тогда и только тогда, когда оно является доминирующим.

 

4.9.1. Нахождение всех максимальных независимых множеств

 

Задача отыскания экстремальных независимых и покрывающих множеств возникает во многих практических случаях. Например, пусть есть множество процессов, использующих неразделяемые ресурсы. Соединим ребрами вершины, соответствующие процессам, которым требуется один и тот же ресурс. Тогда β0 будет определять количество возможных параллельных процессов.

Примером задачи, в которой требуется отыскать максимальные независимые множества, является известная задача о восьми ферзях: расставить на шахматной доске 8 ферзей так, чтобы они не били друг друга. Для решения достаточно представить доску в виде графа с 64 вершинами (соответствующими клеткам доски), которые смежны, если клетки находятся на одной вертикали, горизонтали или диагонали.

Нахождение всех максимальных независимых множеств можно осуществить последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность (путем добавления к исследуемому множеству дополнительной, не принадлежащей ему вершины и выяснением того, сохраняется ли независимость) и запоминанием максимальных множеств. С увеличением числа вершин этот метод поиска становится с вычислительной точки зрения громоздким, поэтому его удобно использовать только для небольших графов, например, с числом вершин, не превосходящих 20. Однако число максимальных независимых множеств увеличивается, но при выполнении процедуры большое число независимых множеств формируется, а затем вычеркивается, так как обнаруживается, что они содержатся в других, ранее полученных множествах, и поэтому не являются максимальными.

Используем систематический метод перебора Брона и Кэрбоша [2], который позволяет обходить указанные трудности. В этом методе не нужно запоминать генерируемые независимые множества для проверки их на максимальность путем сравнения с ранее сформированными множествами.

Введем необходимые обозначения обоснуем алгоритм нахождения всех максимальных независимых множеств.

В процессе поиска - на некотором этапе k - независимое множество вершин Sk расширяется путем добавления к нему подходящим образом выбранной вершины (чтобы получилось новое независимое множество Sk +1) на этапе k +1, и так поступают до тех пор, пока добавление вершин станет невозможным, а порожденное множество не станет максимально независимым множеством. Пусть Qk будет на этапе k наибольшим множеством вершин, для которого Sk ∩ Qk =Æ, то есть после добавления любой вершины из Qk в Sk получится независимое множество Sk +1. В некоторый произвольный момент работы алгоритма множество Qk состоит из вершин двух типов: подмножества Qk - тех вершин, которые уже использовались в процессе поиска для расширения множества Sk, и подмножества Qk + таких вершин, которые еще не использовались. Тогда дальнейшее ветвление в дереве поиска включает процедуру выбора вершины xik Î Qk +, добавления ее к Sk

Sk +1 = Sk È{ xik }

и порождения новых множеств:

Qk -+1 = Qk - \ Г (xik);

Qk ++1 = Qk + \ (Г (xik) È { xik }).

Шаг возвращения алгоритма состоит в удалении вершины xik из Sk +1, чтобы вернуться к Sk, изъятии xik из старого множества Qk + и добавлении xik к старому множеству Qk - для формирования новых множеств Qk - и Qk +.

Множество Sk является максимально независимым множеством только тогда, когда невозможно его дальнейшее расширение, то есть когда Qk +=Æ. Если Qk -¹Æ, то текущее множество Sk было расширено на некотором предшествующем этапе работы алгоритма путем добавления вершины из Qk -, и поэтому не является максимальным независимым множеством. Таким образом, необходимым и достаточным условием того, что Sk - максимально независимое множество, является выполнение равенств:

Qk + = Qk - = Æ.

Если очередной этап работы алгоритма наступает тогда, когда существует некоторая вершина x Î Qk -, для которой Г(x)Ç Qk +=Æ, то безразлично, какая из вершин, принадлежащих Qk +, использовалась для расширения Sk, и это справедливо при любом числе дальнейших ветвлений. Вершина x не может быть удалена из Qp - на любом следующем шаге p > k. Таким образом, существование x, такого что

х Î Qk - и Г (x)Ç Qk + = Æ (4.5)

 

является достаточным для применения шага возвращения, потому что из Sk при всяком дальнейшем ветвлении уже не получится максимально независимое множество.

Если k =0, то возвращение выполнить невозможно, поэтому при k =0 осуществляется переход на прямой шаг.

Опишем алгоритм нахождения всех максимальных независимых множеств вершин графа.

Начальная установка.

Шаг 1.Пусть S0 = Q0 - = Æ, Q 0+= X, k =0.

Прямой шаг.

Шаг 2.Выбрать вершину xik Î Qk + и сформировать Sk +1, Qk -+1 и Qk ++1, оставив Qk - и Qk + нетронутыми. Положить k = k +1.

Проверка.

Шаг 3.Если выполняется условие (4.5), то перейти к шагу 5 иначе к шагу 4.

Шаг 4. Если Qk += Qk - =Æ, то напечатать максимальное независимое множество Sk и перейти к шагу 5. Если Qk +=Æ, а Qk -¹Æ, то перейти к шагу 5, иначе - к шагу 2.

Шаг возвращения.

Шаг 5.Положить k = k –1. Удалить xik из Sk +1, чтобы получить Sk. Исправить Qk + и Qk -, удалив вершину xik из Qk + и добавив ее к Qk -. Если k ¹0, то перейти к шагу 3, иначе если Q0 +=Æ, то остановиться (к этому моменту будут напечатаны все максимальные независимые множества), иначе перейти к шагу 2.

Пример. Найти все максимальные независимые множества графа G.

 

Матрица смежности графа G:

 

  А =   x1 x2 x3 x4 x5 x6 x7
x1              
x2              
x3              
x4              
x5              
x6              
x7              

 

1. Начальная установка:

S 0 = Ø; Q 0- = Ø; Q 0+ = { x 1, x 2, x 3, x 4, x 5, x 6, x 7}; k =0.

2. Прямой шаг:

x 1; S 1 = { x 1}; Q 1- = Ø; Q 1+ = { x 4, x 5, x 6, x 7}; k = 1.

3. Проверка.

Условие не выполняется, переходим к шагу 4 (→ 4).

4. Условие не выполняется → 2.

2. x 4; S 2 = { x 1, x 4}; Q 2- = Ø; Q 2+ = { x 7}; k = 2.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 7; S 3 = { x 1, x 4, x 7}; Q 3- = Ø; Q 3+ = Ø; k = 3.

3. Условие не выполняется → 4.

4. S3 = {x1, x4, x7} - максимальное независимое множество → 5.

5. k = 2; S 2 = { x 1, x 4}; Q 2- = { x 7}; Q 2+ = Ø → 3.

3. Условие выполняется → 5.

5. k = 1; S 1 = { x 1}; Q 1- = { x 4}; Q 1+ = { x 5, x 6, x 7} → 3.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 5; S 2 = { x 1, x 5}; Q 2- = Ø; Q 2+ = { x 6}; k = 2.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 6; S 3 = { x 1, x 5, x 6}; Q 3- = Ø; Q 3+ = Ø; k = 3.

3. Условие не выполняется → 4.

4. S3 = {x1, x5, x6} - максимальное независимое множество → 5.

5. k = 2; S 2 = { x 1, x 5}; Q 2- = { x 6}; Q 2+ = Ø → 3.

3. Условие выполняется → 5.

5. k = 1; S 1 = { x 1}; Q 1- = { x 4, x 5}; Q 1+ = { x 6, x 7} → 3.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 6; S 2 = { x 1, x 6}; Q 2- = { x 5}; Q 2+ = Ø; k = 2.

3. Условие выполняется → 5.

5. k = 1; S 1 = { x 1}; Q 1- = { x 4, x 5, x 6}; Q 1+ = { x 7} → 3.

3. Условие выполняется → 5.

5. k = 0; S 0 = Ø; Q 0- = { x 1}; Q 0+ = { x 2, x 3, x 4, x 5, x 6, x 7} → 2.

2. x 2; S 1 = { x 2}; Q 1- = Ø; Q 1+ = { x 3, x 5, x 7}; k = 1.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 3; S 2 = { x 2, x 3}; Q 2- = Ø; Q 2+ = Ø; k = 2.

3. Условие не выполняется → 4.

4. S2 = {x2, x3} — максимальное независимое множество → 5.

5. k = 1; S 1 = { x 2}; Q 1- = { x 3}; Q 1+ = { x 5, x 7} → 3.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 5; S 2 = { x 2, x 5}; Q 2- = Ø; Q 2+ = Ø; k = 2.

3. Условие не выполняется → 4.

4. S2 = {x2, x5} — максимальное независимое множество → 5.

5. k = 1; S 1 = { x 2}; Q 1- = { x 3, x 5}; Q 1+ = { x 7} → 3.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 7; S 2 = { x 2, x 7}; Q 2- = Ø; Q 2+ = Ø; k = 2.

3. Условие не выполняется → 4.

4. S2 = {x2, x7} — максимальное независимое множество → 5.

5. k = 1; S 1 = { x 2}; Q 1- = { x 3, x 5, x 7}; Q 1+ = Ø → 3.

3. Условие выполняется → 5.

5. k = 0; S 0 = Ø; Q 0- = { x 1, x 2}; Q 0+ = { x 3, x 4, x 5, x 6, x 7} → 3.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 3; S 1 = { x 3}; Q 1- = { x 2}; Q 1+ = { x 4, x 6}; k = 1.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 4; S 2 = { x 3, x 4}; Q 2- = Ø; Q 2+ = Ø; k = 2.

3. Условие не выполняется → 4.

4. S2 = {x3, x4} — максимальное независимое множество → 5.

5. k = 1; S 1 = { x 3}; Q 1- = { x 2, x 4}; Q 1+ = { x 6} → 3.

3. Условие не выполняется → 4.

4. Условие не выполняется → 2.

2. x 6; S 2 = { x 3, x 6}; Q 2- = Ø; Q 2+ = Ø; k = 2.

3. Условие не выполняется → 4.

4. S2 = {x3, x6} — максимальное независимое множество → 5.

5. k = 1; S 1 = { x 3}; Q 1- = { x 2, x 4, x 6}; Q 1+ = Ø → 3.

3. Условие выполняется → 5.

5. k = 0; S 0 = Ø; Q 0- = { x 1, x 2, x 3}; Q 0+ = { x 4, x 5, x 6, x 7} → 2.

2. x 4; S 1 = { x 4}; Q 1- = { x 1, x 3}; Q 1+ = { x 7}; k = 1.

3. Условие выполняется → 5.

5. k = 0; S 0 = Ø; Q 0- = { x 1, x 2, x 3, x 4}; Q 0+ = { x 5, x 6, x 7} → 2.

2. x 5; S 1 = { x 5}; Q 1- = { x 1, x 2}; Q 1+ = { x 6}; k = 1.

3. Условие выполняется → 5.

5. k = 0; S 0 = Ø; Q 0- = { x 1, x 2, x 3, x 4, x 5}; Q 0+ = { x 6, x 7} → 2.

2. x 6; S 1 = { x 6}; Q 1- = { x 1, x 3, x 5}; Q 1+ = Ø; k = 1.

3. Условие выполняется → 5.

5. k = 0; S 0 = Ø; Q 0- = { x 1, x 2, x 3, x 4, x 5, x 6}; Q 0+ = { x 7} → 2.

2. x 7; S 1 = { x 7}; Q 1- = { x 1, x 2, x 4}; Q 1+ = Ø; k = 1.

3. Условие выполняется → 5.

5. k = 0; S 0 = Ø; Q 0- = { x 1, x 2, x 3, x 4, x 5, x 6, x 7}; Q 0+ = Ø → останов.

Таким образом, данный граф имеет семь максимальных независимых множеств:

S1 = {x1, x4, x7}; S2 = {x1, x5, x6}; S3 = {x2, x3}; S4 = {x2, x5}; S5 = {x2, x7}; S6 = {x3, x4}; S7 = {x3, x6}.

Ядро - множество, которое является одновременно минимальным доминирующим и максимальным независимым.

Утверждение 4.9.1. Конечный граф без петель, не содержащий контуров нечетной длины, обладает ядром.

Понятие, противоположное максимальному независимому множеству, есть максимальный полный подграф. Максимальный полный подграф графа G называется кликой графа. Следовательно, в противоположность максимальному независимому множеству, в котором не могут встретиться две смежные вершины, в клике все вершины попарно смежны. Совершенно очевидно, что максимальное независимое множество графа G соответствует клике графа 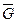и наоборот, где 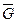– дополнение графа G.

Кликовое число – максимальное число вершин в кликах данного графа.

Утверждение. 4.9.2. Максимальное независимое множество графа G соответствует клике графа `G и наоборот.

Покрытия и раскраски

 

Некоторые задачи, возникающие при планировании производства, составлении графиков осмотра и транспортировки товаров, могут быть представлены как задачи теории графов, тесно связанные с так называемой «задачей раскраски». Эта задача формулируется следующим образом: для данного графа определить минимальное количество цветов, необходимых для раскраски вершин графа так, чтобы никакие две смежные вершины не были окрашены в один цвет.

Задачи раскраски вершин или ребер графа занимают важное место в теории графов. К построению раскрасок сводится целый ряд практических задач. Характерной особенностью этих задач является существование объек­тов, которые по каким-либо причинам не могут быть объ­единены в одну группу.

Пусть G – некоторый граф, k – натуральное число. Произвольная функция вида f: X ®{l,2,..., k }назы­вается вершинной k-раскраской, или просто k-раскраской, графа G. Если позволяет контекст, то k в этом определе­нии опускается. Раскраска называется правильной, если f(xi) ¹ f(xj) для любых смежных вершин xi и xj. Граф, для которого существует правильная k -раскраска, называется k-раскрашиваемым (или раскрашиваемым k цветами). В определении раскраски вместо множества {1, 2,..., k }можно взять произвольное k -элементное множество.

Правильную k -раскраску графа можно трактовать как окрашивание каждой его вершины в один из k цветов, при этом смежные вершины должны получать различ­ные цвета. Поскольку функция f не обязательно сюрьективна, то при k -раскраске фактически может быть ис­пользовано менее k цветов. Таким образом, правильную k -раскраску графа G можно рассматривать как разбие­ние

X 1È X2 È... È Xl = X, l£k,

множества вершин X на не более чем k непустых клас­сов, каждый из которых является независимым множест­вом. Классы этого разбиения называются цветными классами. Множество вершин одного цвета называетсяодноцветным клаcсом.

Минимальное число k, при котором граф G является k -раскрашиваемым, называется хроматическим числом этого графа и обозначается (G). Если (G) = k, то граф G называется k-хроматическим. Правильная k -раскраска графа G при k= (G) называется минимальной.

В качестве иллюстрации рассмотрим граф G, изобра­женный на рис. 4.28, где указана одна из правильных 4-раскрасок. Меньшим числом цветов этот граф раскра­сить правильно нельзя. Действительно, граф содержит цикл (x1, x2, x3, x4, x5, x1), для правильной раскраски которого нужно не менее трех цветов, а для вершины x6 требуется новый цвет. Итак, g(G)=4.

 

 

Пример. Так как в полном графе Кп любые две различные вершины связаны ребром, то g (Кn)= п.

Рассмотрим некоторые практи­ческие задачи, сводящиеся к пра­вильной раскраске графов.

1. Задача составления расписа­ний. Предположим, что нужно про­честь несколько лекций за крат­чайшее время. Чтение каждой лек­ции в отдельности занимает один час, но некоторые лекции не мо­гут читаться одновременно (например, их читает один и тот же лектор). Построим граф G, вершины которого би­ективно соответствуют лекциям, и две вершины смежны тогда и только тогда, когда соответствующие лекции нель­зя читать одновременно. Очевидно, что любая правильная раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам графа, составляющим цветной класс, читаются одновременно. И, обратно, любое допустимое расписание определяет правильную раскраску графа G. Оптимальные расписания соответствуют мини­мальным раскраскам, а число часов, необходимое для про­чтения всех лекций, равно g (G).

2. Задача распределения оборудования. Заданы мно­жества Х = { х1, х2,..., хn }и S = { s1, s2,..., sm }работ и механизмов соответственно. Для выполнения каждой из работ требуется некоторое время, одинаковое для всех работ, и некоторые механизмы. При этом никакой из ме­ханизмов не может быть одновременно занят в несколь­ких работах. Нужно распределить механизмы так, чтобы общее время выполнения всех работ было минимальным. Построим граф G с множеством вершин X и объявим верши­ны хi и хj (i≠j) смежными тогда и только тогда, когда для выполнения работ хi и хj требуется хотя бы один общий механизм. При правильной раскраске графа G ра­боты, соответствующие вершинам одного цвета, можно выполнять одновременно, а наименьшее время выполне­ния всех работ достигается при минимальной раскраске.

3. Задача о проектировании коробки скоростей. Короб­ка скоростей – механизм для изменения частоты враще­ния ведомого вала при постоянной частоте вращения ве­дущего. Это изменение происходит за счет того, что на­ходящиеся внутри коробки шестерни (зубчатые колеса) вводятся в зацепление специальным образом. Одна из задач, стоящая перед конструктором коробки, заключает­ся в минимизации ее размеров, а это часто сводится к минимизации числа валов, на которых размещаются шестерни.

Построим граф G, вершины которого биективно соот­ветствуют шестерням. Если по какой-то причине две шестерни не должны находиться на одном валу (напри­мер, они могут быть в зацеплении, или их общий вес велик для одного вала и т. д.), то соответствующие вер­шины графа соединим ребром. Вершины, имеющие один цвет при правильной раскраске этого графа, определяют шестерни, которые могут находиться на одном валу, а хроматическое число g (G) равно минимальному коли­честву валов, нужных для проектируемой коробки.

4. Рассмотрим граф G, вершины которого – страны, а ребра соединяют страны, имеющие общую границу. Числу g (G) соответствует наименьшее число красок, необходимых для раскраски карты так, чтобы никакие две соседние страны не были окрашены в один цвет.

Для некоторых графов хроматические числа найти не­сложно. Например, g (Кп) = п, g(Kn,m) = 2, g(C2n) = 2, g(C 2 n +1) = 3.

Очевидно, что граф является 1-хроматическим тогда и только тогда, когда он пустой, а 2-хроматическим – когда он двудольный и непустой. Обычно 2-хроматический граф называют бихроматическим.Поэтому теорему Кёнига о двудольных графах можно сформулировать в следующем виде.

Теорема 4.10.1. Непустой граф является бихроматическим тогда и только тогда, когда он не содержит цик­лов нечетной длины.

Задачи определения хроматического числа и построе­ния минимальной раскраски произвольного графа явля­ются очень сложными, эффективные алгоритмы их ре­шения неизвестны. Рассмотрим простой эвристический алгоритм построе­ния правильной раскраски вершин графа, в ряде случаев приводящий к раскраскам, близким к минимальным.

Замечание. Данный алгоритм определяет оценку y '(G) хроматического числа g(G) графа G, которая удовлетворяет соотношению

g(G) £y'(G) £ max min { d (i)+l, i },

i

где d (i) – степень i -ой вершины, причем индексация вершин хi осуществляется в соответствии с убыванием их степеней.

Шаг 1. G – данный граф. Для каждой вершины графа определить ее степень. Расположить вершины в порядке невозрастания их степеней.

Шаг 2. Первая вершина окрашивается в цвет №1. Затем список вершин просматривается сверху вниз и в цвет №1 окрашивается всякая вершина, которая не смежна с другой, уже окрашенной в этот цвет.

Шаг 3. Возвращаемся к первой в списке неокрашенной вершине, окрашиваем ее в цвет №2 и, двигаясь по списку, окрашиваем вершины в цвет №2 так же, как окрашивали в цвет №1.

Шаг 4. Процедура продолжается до тех пор, пока все вершины не будут окрашены. Количество использованных цветов будет приближенным значением хроматического числа.

Раскраска, к которой приводит описанный алгоритм, называется последовательной. Очевидно, что это – пра­вильная раскраска. Для некоторых классов графов (на­пример, полных k -дольных) последовательная раскраска является минимальной. В общем случае это не так.

Следующая теорема сводит задачу построения пра­вильной раскраски графов к аналогичной задаче для двухсвязных графов.

Теорема 4.10.2. Если каждый блок графа k -раскраши-ваем, то и сам граф также k -раскрашиваем.

Доказательство. Воспользуемся индукцией по числу блоков рассмат­риваемого графа. Для графа, являющегося блоком, ут­верждение тривиально. Предположим, что теорема верна для графов, состоящих из m /1 блоков. Пусть теперь G – граф, имеющий ровно m+ 1 блоков, В – один из его концевых блоков, Н – объединение всех остальных бло­ков. По индуктивному предположению оба графа В и H являются k -раскрашиваемыми. Зафиксируем для каждого из них правильную k -раскраску.

Графы В и H имеют ровно одну общую вершину х. Если ее цвета в обеих фиксированных k -раскрасках сов­падают, то получена правильная k -раскраска графа G. В противном случае нужно очевидным образом переста­вить цвета в одной из фиксированных раскрасок. Теорема доказана.

Утверждение 4.10.1. Если граф G является r -хромати-ческим, то он может быть раскрашен с использованием r красок с помощью следующей процедуры: сначала в один цвет окрашивается некоторое максимальное независимое множество S [ G ], затем окрашивается в следующий цвет множество S [ X \ S [ G ]] и т.д. до тех пор пока не будут раскрашены все вершины.

Утверждение 4.10.2. Каждый планарный граф 5-раскра-шиваем.

Утверждение 4.10.3. Каждый планарный граф, не содержащий треугольников, 3-раскрашиваем.

Утверждение 4.10.4. Хроматическое число графа G равно кликовому числу его дополнения ` .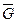

Реберной раскраской неорграфа G =(X, V) k цветами называется функция

j: V ®{l,2,.., k },

такая, что для любых двух смежных ребер v1 и v2 выполняется j (v 1)¹ j (v 2).

Хроматическим индексом графа G называется наименьшее такое k, что граф G допускает реберную раскраску k цветами.

Существуют и практические задачи, связанные с раскраской ребер в мультиграфе.

Раскраска ребер в мультиграфе G может быть определена с помощью раскраски вершин так называемого реберного мультиграфа L(G). Для произвольного неориентированного мультиграфа G={X, V, Р}, где X – множество вершин, V – множество дуг, Р Î V X V, (x,v,y) Î Р тогда и только тогда, когда дуга v исходит из вершины х и заходит в вершину у, реберным мулътиграфом L(G) называется тройка { V, X, Р’}, где Р'ÎV X V, и выполняется (u, х, v)ÎР' тогда и только тогда, когда в мультиграфе G вершина х является концом ребер и и v. Раскраской ребермультиграфа G называется раскраска вершин мультиграфа L(G).

Пример. Проводится монтаж аппаратуры. Чтобы не перепутать проводники, необходимо их окрасить таким образом, чтобы два проводника, идущие к одной плате, имели разные цвета. В этом случае вершинами являются платы, а ребрами – проводники.

Теорема 4.10.3. Пусть G –неорграф без петель, имеющий хотя бы одно ребро. Тогда следующие условия эквивалентны:

1) G – бихроматический граф;

2) G – двудольный граф;

3) G не содержит циклов нечетной длины.

Теорема 4.10.4.Для любого неорграфа G без петель выпол­няется неравенствоg (G) £ d(G) +1, где d(G) – наибольшая степень вершин графа.

 

 
Поделиться:





Воспользуйтесь поиском по сайту:



©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...