Сочетание из n элементов по k

Сочетание без повторений. Пусть дано множество Х={x₁;x₂;...;x_n} и множество Y={y₁; y₂;...;y_k}. Сколько существует подмножеств множества Х мощности k, отличающихся между собой хотя бы одним элементом?

Число сочетаний из n по k без повторения определяют по формуле:

 

Пример: пусть дано множество {a, b, c, d}. Сколько и какие подмножества можно сформировать для n=4 и k=3?

Число сочетаний из 4 по 3 без повторения равно

,

а множество комбинаторных объектов:

C43={{a, b, c}; {a, b, d}; {a, c, d}; {b, c, d}}.

Пример: каждому играющему в домино выдается 7 костей из 28. Сколько существует различных комбинаций костей, которые игрок может получить в начале игры?

Число возможных комбинаций в начале игры определяется числом сочетаний из 28 костей по 7, т. е. .

Сочетание с повторением. Отличием такой комбинаторной операции является возможность многократного использования в выборке, но не более k раз, одного и того же элемента множества Х. Число сочетаний с повторением равно:

,

 

а множество возможных комбинаторных объектов есть

С_{n повт}^k={{x₁, x₁, x₁,..}; {x₁, x₂, x₂,..}; {x₂, x₂, x₃,..}..}.

 

Пример: пусть Х={a, b, c, d}. Сколько и какие подмножества можно сформировать из четырех элементов по три с повторением?

Число сочетаний

а множество комбинаторных объектов:

С_3.²= {{a, a, a}; {b, b, b}; {c, c, c}; {d, d, d}; {a, a, b}; {a, a, c}; {a, a, d};

{ b, b, a}; {b, b, c}; {b, b, d}; { c, c, a}; { c, c, b}; {c, c, d}; {d, d, a,}; {d, d, b}; {d, d, c}; {a, b, c}; {a, b, d}; {a, c, d}; {b, c, d}}.

Разбиение множества

Число Стирлинга второго рода. Если Y есть набор подмножеств Y={Y₁;Y₂;...;Y_k}, то отображение множества Х={x₁;x₂;...;x_n} на Y определит разбиение множества X на подмножества Х₁;Х₂;...;Х_k, при выполнении следующих условий:

 

_i=1 È ^kX_i=X;

X_i Ç X_j=Æ, для i¹j; 1£i, j£k;

X_i¹Æ, для 1£i£k;

|X₁|+|X₂|+...+|X_k| = |X| = n.

Каждое подмножество Х_i называют блоком разбиения множества Х, а само разбиение обозначают B _k(Х)={Х₁; Х₂;...;Х_k}.

Число возможных разбиений множества Х на подмножества определяют числом Стирлинга второго рода S(n; k), где n - мощность множества X, а k –число формируемых подмножеств по правилу:

 

S(n; 0)=0 для n>0; S(n; n)=1 для n³0; S(n; k)=S(n-1; k-1)+t×S(n-1; k) для 0<k£n.

Пример: дано множество Х={a, b, c, d}. Выполнить его разбиение на два одноэлементных подмножества и одно двухэлементное, т.е. Y={Y₁, Y₂, Y₃}, где |Y₁|=1, |Y₂|=1, |Y₃|=2. Сколько и какие подмножества можно сформировать?

Число разбиений по формуле Стирлинга равно:

S(4, 3)=S(3, 2)+3×S(3, 3)=S(3, 2)+3, S(3, 2)=S(2, 1)+2×S(2, 2)=S(2, 1)+2; S(2, 1)=S(1, 0)+1×S(1, 1)=0+1.

S(4, 3)=3+2+1=6,

а множество подмножеств есть:

B ₃(4)={{{a}, {b}, {c, d}}; {{a}, {c}, {b, d}}; {{a}, {d}, {b, c}}; {{b}, {c}, {a, d}}; {{b}, {d}, {a, c}}; {{c}, {d}, {a, b}}}.

Пример: дано множество Х={a, b, c, d, e, f}. Разбить на два трехэлементных подмножества, т.е. Y={Y₁; Y₂}, где |Y₁|=3; |Y₂|=3. Сколько подмножеств можно сформировать?

Число таких разбиений по формуле Стирлинга равно:

S(6, 2)=S(5, 1)+2×S(5, 2),

S(5, 2)=S(4, 1)+2×S(4, 2),

S(5, 1)=S(4, 0)+1×S(4, 1)= S(4, 1),

S(4, 2)=S(3, 1)+2×S(3, 2),

S(4, 1)=S(3, 0)+1×S(3, 1)= S(3, 1).

S(3, 2)=S(2, 1)+2×S(2, 2)= S(2, 1)+2,

S(3, 1)=S(2, 0)+1×S(2, 1)= S(2, 1),

S(2, 1)= S(1, 0)+1×S(1, 1)=0+1=1.

S(6, 2)= 1+2×15=31.

Следовательно, существует 31 способ разбиения шестиэлементного множества на два трехэлементных подмножества.

Булеан множества. Множество подмножеств универсального множества U, включающее в себя пустое подмножество, одно-, двух- и т. д. до n-элементного подмножества, называют булеаном B (U). Каждое подмножество формируется сочетанием без повторения элементов универсального множества |U|=n по числу элементов формируемого подмножества i=0, 1, 2,..n.

, где i= 0, 1, 2,...n.

Пример: дано U={a, b, c, d}.

Булеан множества U есть B (U)={Æ; {a}; {b}; {c}; {d}; {a, b};

{a, c}; {a, d}; {b, c}; {b, d}; {c, d}; {a, b, c}; {a, b, d}; {b, c, d}; {a, c, d}; {a, b, c, d}}.

Правила комбинаторики

При исполнении нескольких операций (размещений, перестановок, сочетаний или разбиений) следует применять дополнительные правила: суммы, произведения и включения-исключения.

Правило суммы: если комбинаторный объект t _i может быть выбран из исходного множества X “ s ” способами, а другой комбинаторный объект t _j из того же исходного множества X “ p ” способами, то выбор “либо t _i, либо t _j“ может быть осуществлен “(s + p)” способами.

Пример: сколько можно составить перестановок из n перфокарт, в которых две перфокарты ‘a’ и ‘b’ не стояли бы рядом?

Известно, что общее число перестановок равно n!.

Если ‘a’ стоит непосредственно перед ‘b’, то раcположение пары ‘a, b’ среди множества перфокарт равно (n-1). Если ‘b’ стоит непосредственно перед ‘a’, то раcположение пары 'b, a’ среди множества перфокарт также равно (n-1).

По правилу суммы общее число размещений рядом перфокарт “a” и “b” равно (n-1)+(n-1)=2(n-1).

Число перестановок оставшихся перфокарт для каждого случая, когда перфокарты ’a’ и ‘b’ стоят рядом, равно (n-2)!

По правилу суммы общее число перестановок, когда перфокарты ‘a’ и ‘b’ стоят рядом, равно 2(n -1)×(n -2)! = 2(n -1)!

Следовательно, искомое число перестановок равно

n! - 2(n -1)!=(n-2)×(n -1)!

Пусть даны четыре перфокарты X={a, b, c, d}. Число перестановок, когда карты ‘a’ и ‘b’ не стоят рядом, равно

(4-2)(4-1)!=12.

Множество комбинаторных объектов по этому условию есть:

{(a c b d), (a c d b), (a d b c), (a d c b), (b c a d), (b c d a), (b d a c),

(b d c a), (c a d b), (c b d a), (d a c b), (d b c a)}.

Правило произведения: если комбинаторный объект t _i может быть выбран из исходного множества “ s ” способами и после каждого из таких выборов комбинаторный объект t _j может быть выбран “ p ” способами, то выбор “ t _i и t _j“ в указанном порядке может быть осуществлен “(s × p)” способами.

Пример: Из m букв и n цифр следует сформировать k элементные множества, содержащие s букв и (k-s) цифр при условии s £ m, (k-s)£ n.

Число подмножеств, содержащих s букв, есть

.

Число подмножеств, содержащих (k-s) цифр есть .

 

Тогда число подмножеств, содержащих s букв и (k-s) цифр, по правилу умножения есть

 

Пусть даны четыре буквы {a, b, c, d} и три цифр {1, 2, 3}, для которых m =4 и n =3. Сформировать трехэлементные подмножества (k =3), содержащих две буквы (s =2) и одну цифру ((к-s)=1).

Число трехэлементных комбинаторных объекта, содержащих две буквы и одну цифру равно:

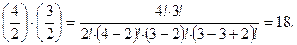
Множество таких объектов:

{{a, b, 1}, {a, b, 2}, {a, b, 3}, {a, c, 1}, {a, c, 2}, {a, c, 3}, {a, d, 1}, {a, d, 2}, {a, d, 3}, {b, c, 1}, {b, c, 2}, {b, c, 3}, {b, d, 1}, {b, d, 2}, {b, d, 3}, {c, d, 1}, {c, d, 2}, {c, d, 3}}.

Правило включения-исключения: если существует множество объектов Х и множество свойств Y={y₁,y₂,..y_t}, которыми могут обладать элементы x_iÎХ, то может быть выполнено разбиение множества Х на подмножества по числу свойств, которыми они обладают.

В этом случае разбиение множества на подмножества удовлетворяет следующему условию:

|X₀|=|X|-|X₁|+|X₂|-|X₃|...+(-1)^t|X_t|,

где |X₀| - число элементов множества Х, не обладающих ни одним свойством множества Y;

|X | - общее число элементов множества Х;

|X₁| - число элементов множества Х, обладающих только одним свойством из множества Y, т.е. y_iÎY;

|X₂| - число элементов множества Х, обладающих только двумя свойствами множества Y, т.е. {y_i, y_j}ÍY;

|X₃| - число элементов множества Х, обладающих только тремя свойствами множества Y, т.е. {y_i, y_j, y_k}ÍY и т.д.

Следует обратить внимание, что знак “+” ставят для подмножеств, обладающих четным числом свойств, а знак “-” - нечетным.

Пример: даны множества A, B и C. При этом xÎA, xÎB, xÎC, xÎ(AÇB), xÎ(AÇC), xÎ(BÇC) или xÎ(AÇBÇC). Найти xÎ(AÈBÈC).

Согласно правилу включения-исключения имеем:

Æ=|AÈBÈC|-|A|-|B|-|C|+|(AÇB)|+|(AÇC)|+|(BÇC)|-|AÇBÇC)|.

Откуда |AÈBÈC|=|A|+|B|+|C|-|(AÇB)|-|(AÇC|-|BÇC|+ |AÇBÇC)|.

Пусть даны по четыре прописных буквы латиницы A’={A, B, C, D},

кириллицы А”={А, Б, В, Г} и греческого алфавита А’”={А, B, Γ, Δ}.

Тогда (A'ÇА”)={A, B}, (A’ÇА”)={A, B},

(А”ÇА’”)={A, В, Г},

Рис. 2.1 Поиск объединения множеств (A’ÇА”ÇА’”)={A, B}.

Следовательно, |A’ÈА”ÈА’”|=|A’|+|А”|+|А’”|-|(A’ÇА”)|-|(A’ÇА’”)|-|(А”ÇА’”)|+|(A’ÇА”ÇА’”)|= 4+4+4-2-2-3+2 =7.

Множество букв объединения четырех алфавитов есть (A’ÈА”ÈА’”) = {A, B, C, D, Б, Г, Δ}.

Пример: Дана колода из n индексированных перфокарт. Сколькими способами можно расположить их в колоде, чтобы ни одна перфокарта с номером i не занимала i-го места? для 1£i£n.

Общее число перестановок перфокарт в колоде равно n!

Число перестановок, при котором i перфокарт занимают i мест есть (n-i)!

Число перестановок i перфокарт, когда i-я перфокарта занимает i-е место по правилу произведения равно:

.

И наконец, число размещений перфокарт

в колоде, при котором ни одна из перфокарт с номером i не занимает i-го места по правилу включения-исключения равно:

 

B₀ .

 

Пусть n=4.

Тогда B ₀ ..

В таблице приведены возможные расположения перфокарт, когда ни одна перфокарта не занимает соответствующего места.

Пример: в студенческой группе обучается 50 человек, т.е. |X|=50. В группе 20 юношей (свойство -”быть юношей”), т.е. |X₁₁|=20, 20 студентов имеют хорошую успеваемость (свойство -”быть успевающим”), т.е. |X₁₂|=20, 20 студентов увлекаются спортом (свойство -”быть спортсменом”), т.е. |X₁₃|=20, 5 юношей имеют хорошую успеваемость (два свойства: ”быть юношей” и “быть успевающим”), т.е. |X₂₁|=|X₁₁ÇX₁₂|=5, 10 юношей увлекаются спортом (два свойства: “быть юношей” и “быть спортсменом”), т.е. |X₂₂|=|X₁₁ÇX₁₃|=10, 10 успевающих студентов увлекаются спортом (два свойства: “быть успевающим” и “быть спортсменом”), т.е. |X₂₃|=|X₁₂ÇX₁₃|=10, 5 юношей имеют хорошую успеваемость и увлекаются спортом (три свойства: “ быть юношей”, “быть успевающим” и “быть спортсменом”), т.е. |X₃₁|=|X₁₁ÇX₁₂ÇX₁₃|=5.

Сколько девушек (ùX₁₁) имеют слабую успеваемость (ùX₁₂) и не увлекаются спортом (ùX₁₃) или ù(X₁₁ÇX₁₂ÇX₁₃)?

По правилу включения-исключения имеем:

|ù(X₁₁ÇX₁₂ÇX₁₃)|=|X|-|X₁₁|-|X₁₂|-|X₁₃|+|X₂₁|+|X₂₂|+|X₂₃|-|X₃₁|

|ù(X₁₁ÇX₁₂ÇX₁₃)|=50-20-20-20+5+10+10-5=10.

Следовательно, 10 девушек имеют слабую успеваемость и не увлекаются спортом.

 

Пример: в цехе имеется 9 свободных рабочих мест, из которых на двух могут работать только женщины, а на трех - только мужчины. Сколькими способами можно распределить трех женщин и четырех мужчин на эти рабочие места?

Если трех мужчин направить на три рабочих места, оборудованных для мужчин, без учета их квалификации, то из четырех общих рабочих мест без учета их специализации одно будет занято мужчиной. В этом случае существует три способа размещения женщин на рабочих местах без учета их квалификации и специализации рабочих мест (см. рисунок). Если двух мужчин направить на два специализированных для мужчин рабочих места, то из четырех общих рабочих мест два места будут заняты мужчинами без учета их квалификации. В этом случае существует два способа размещения женщин на рабочих местах без учета их квалификации (см. рисунок).

И наконец, если одного мужчину направить на одно специализированное для мужчин рабочее место, то из 4-х общих свободных рабочих мест три будут заняты мужчинами без учета их квалификации. В этом случае существует один способа размещения женщин на рабочих местах.

Итого существует шесть способов распределения трех женщин и четырех мужчин без учета их квалификации и специализации девяти рабочих мест.

Вопросы и задачи

2.1. Сколько будет четырехзначных чисел из цифр 0, 1, 2, 3?

2.2. Из цифр 1, 2, 3, 4, 5 составить трехзначные числа так, что в каждом числе не было одинаковых цифр.Сколько четных чисел?

2.3. В соревновании участвуют 8 спортсменов. Сколькими способами можно распределить между ними золотую, серебряную и бронзовую медали?

 

2.4. Каково число матриц из n строк и m столбцов с элементами из множества {0, 1}.

 

2.5. Сколькими способами из 28 костей домино можно выбрать две кости так, чтобы их можно было приложить друг к другу (т.е. некоторое число очков встретилось на обеих костях)?

 

2.6. Бросают три игральные кости (с шестью гранями каждая). Сколькими способами они могут упасть так, что все оказавшиеся вверху грани имели одинаковое число очков?

 

2.7. Дано m предметов одного сорта и n –другого. Найти число выборок, составленных из r предметов одного сорта и s –другого.

 

2.8. Из 30 сотрудников отдела английский язык знают 19

человек, немецкий - 17, французский -11, английский и немецкий - 12, английский и французский - 7, немецкий и французский -5, все три языка - 2 человека. Сколько сотрудников не владеют иностранным языком?

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: