 |
Часть 1. Генеральная совокупность и выборка. Статистический ряд распределения и выборочные характеристики.
|
|
|
|
Выборкой называют реально наблюдаемые значения (в том числе и повторяющиеся) случайной величины X, а все теоретически домысливаемые значения этой величины - генеральной совокупностью. Выборку или наблюдаемые значения СВ X обозначают x1, x2,…, xn; n - объем выборки.
С помощью инструмента Сервис / Анализ данных / Генерация случайных чисел удобно моделировать случайные выборки с разными законами распределения вероятности: равномерное распределение, нормальное распределение, Бернулли, биномиальное, Пуассона, модельное, дискретное.
Основными числовыми характеристиками выборки x1, x2,…, xn или выборочными характеристиками, являются:
· выборочное среднее 
;
· выборочная дисперсия 
, которую вычисляют по одной из двух тождественных формул:
,
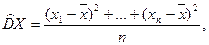
· выборочное среднее квадратическое отклонение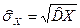 
- это характеристика среднего разброса попавших в выборку чисел около выборочной средней.
Аналогичные характеристики генеральной совокупности называют генеральными характеристиками. Если генеральная совокупность задана рядом распределения вероятностей случайной величины X, то:
· генеральное среднее MX, называемое иначе математическим ожиданием случайной величины X, вычисляется по формуле 
;
· генеральная дисперсия DX вычисляется по одной из двух тождественных формул:
,
,
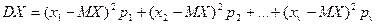· генеральное среднее квадратическое отклонение СВ X вокруг MX – по формуле: 
.
В реальных задачах исследователь располагает, как правило, результатами выборочных наблюдений (статистическими данными) и не знает «всей» генеральной совокупности. Вычисленные по этим данным выборочные характеристики являются оценками соответствующих генеральных характеристик. Будем предполагать, что наблюдения независимы и проведены примерно в одинаковых (типичных) условиях. При выполнении этих предположений выборочное среднее 
является «хорошей оценкой» генерального среднего MX. Более же «хорошей оценкой» генеральной дисперсии DX, особенно при малом объеме выборки, является так называемая «несмещенная оценка» генеральной дисперсии, вычисляемая по формуле
|
|
|
и называемая дисперсией выборки.
Величину 
называют выборочным стандартным отклонением.
ПРИМЕР 1.
В ходе исследования рецидивной преступности из документов были собраны данные о числе повторных судимостей 100 случайно отобранных человек, имевших в прошлом одну или более судимостей. Среди отобранных не имели повторных судимостей 50 человек, а по остальным — числа повторных судимостей оказались такими: 1, 1, 1, 2, 3, 1, 1, 1, 1, 2, 2, 1, 2, 1, 1, 1, 1, 1, 2, 3, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 2, 2, 1, 2, 1, 3, 4, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1.
Чтобы составить представление о закономерности варьирования чисел в «неизвестной» генеральной совокупности, результаты выборочных наблюдений группируют.
Сгруппируем 100 данных о числе повторных судимостей так: различающиеся наблюдения (их называют вариантами, хi) расположим в порядке возрастания и для каждого варианта хi, укажем число mi - частоту (кратность) варианта, число 
= mi/n - частость (относительную частоту, статистическую или опытную вероятность) варианта, вероятность Пуассона рассчитывается по формуле 
:
| Число повторных судимостей (xi) | Итого | |||||
| Количество человек (mi) | ||||||
Опытная вероятность 
| 0,5 | 0,35 | 0,1 | 0,04 | 0,01 | |
| (число людей в %) | 50% | 35% | 10% | 4% | 1% | 100% |
| Вероятность Пуассона (pi) | 0,49 | 0,35 | 0,12 | 0,03 | 0,01 |
Судя по ряду: рецидивистов с двумя судимостями в 3,5 раза больше числа рецидивистов с тремя судимостями; в свою очередь число рецидивистов с тремя судимостями в 2,5 раза больше, чем рецидивистов с четырьмя судимостями.
|
|
|
Распределение опытных (статистических) вероятностей по вариантам:
| Вариант (xi) | 
| |
| Опытная вероятность
| 
| 
|
называют статистическим рядом распределения. В статистическом ряду указывают значения – варианты, зафиксированные в проведенных наблюдениях, и опытные вероятности вариантов, которые могут и не совпадать с истинными вероятностями.
Результат работы «Описательной статистики» представлен в таблице:
| Столбец1 | |
| Среднее | 0,710 |
| Стандартная ошибка | 0,088 |
| Медиана | 0,500 |
| Мода | 0,000 |
| Стандартное отклонение | 0,880 |
| Дисперсия выборки | 0,774 |
| Эксцесс | 1,709 |
| Асимметричность | 1,334 |
| Интервал | 4,000 |
| Минимум | 0,000 |
| Максимум | 4,000 |
| Сумма | 71,000 |
| Счет | 100,000 |
| Уровень надежности(95,0%) | 0,175 |
В таблице приведены:
медиана — число, находящееся в центре ряда данных, расположенных в неубывающем порядке; если в центре этого ряда будет два числа, то медиана равна среднему арифметическому этих чисел;
мода — число, наиболее часто встречающееся в ряду данных;
минимум – минимальный элемент выборки,
максимум – максимальный элемент выборки,
сумма – сумма элементов выборки,
счет – число элементов выборки (объем выборки),
среднее – среднее значение выборки,
стандартная ошибка – погрешность оценки среднего значения,
асимметричность – показывает насколько ассиметрично распределение плотности вероятности,
эксцесс – характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением.
Последнее число в таблице: 0,175 — это ошибка ε выборочного среднего, гарантируемая с 95%-ной надежностью; с вероятностью 95% можно утверждать, что интервал (0,535; 0,885) накроет генеральное среднее число повторных судимостей. Поскольку найденный интервал не накрывает, например, число 1, то гипотезу H0: MX = 1 о том, что генеральное среднее число повторных судимостей равно 1 (при альтернативе H1: MX ≠ 1), принять, на уровне значимости α = 1-γ = 1-0,95 = 0,05, нельзя.
«Гистограмма»:
· группирует числа, введенные в рабочий лист, при этом граничные значения – «карманы» либо вводятся в рабочий лист в возрастающем порядке, либо рассчитываются автоматически (как точки, равномерно распределенные между минимальным и максимальным наблюдениями), а частота текущего «кармана» - это число наблюдений, не больших этого «кармана» и больших предыдущего «кармана»;
|
|
|
· подсчитывает по требованию «интегральный %» - это ряд накопленных частостей (опытных вероятностей) в процентах;
· строит по требованию гистограмму – столбиковую диаграмму частот и график «интегральных %» (Рис.2).
В таблице представлены результаты «Гистограммы» для 100 данных о числе повторных судимостей при введенных граничных значениях 0, 1, 2, 3, 4.
| Карман | Частота | Интегральный % |
| 50,00% | ||
| 85,00% | ||
| 95,00% | ||
| 99,00% | ||
| 100,00% | ||
| Еще | 100,00% |
Рис.2. Результат работы средства Гистограмма
Приводимая в распечатке работы средства «Описательная статистика» асимметричность (А) является характеристикой асимметричности гистограммы (если правая ветвь длиннее левой, А > 0; в противном — А < 0), а эксцесс (Е) является характеристикой «островершинности» гистограммы по сравнению с нормальной кривой (чем больше Е, тем «островершиннее» гистограмма). Для нормальной кривой А = Е = 0.
Обратим внимание на то, что выборочное среднее число судимостей ( = 0,71) примерно равно дисперсии числа судимостей (
— 0,77). Это служит основанием выдвижения гипотезы H0: СВ X (число повторных судимостей случайно выбранного человека, имеющего в прошлом судимость) имеет пуассоновское распределение. Математическое ожидание Mm (в условиях примера Mm — это генеральное среднее число повторных судимостей) и дисперсия Dm (генеральная дисперсия числа повторных судимостей) этого распределения совпадают. Пуассоновские вероятности, где а = Mm заменено на выборочное среднее число повторных судимостей, а ≈ = 0,71, приведены в последней строке. Пуассоновские вероятности практически не отличаются от опытных, гипотеза H0 согласуется с результатами наблюдений.
Для выявления закономерности варьирования наблюдений в случае большого числа вариантов, что обычно бывает при изучении непрерывной величины (например, времени, прошедшего между освобождением рецидивиста из мест лишения свободы и совершением нового преступления) строят интервальный статистический ряд.
|
|
|
ПРИМЕР 2.
По документам n = 100 рецидивистов собраны сведения о времени X между окончанием меры наказания за первое преступление и привлечением к наказанию за второе преступление. Отметим, что число различающихся данных оказалось достаточно большим, при этом x min = 0 (рецидивист совершил второе преступление до окончания меры наказания за первое), а x max = 7,5 (лет). Длину h интервала группирования сведений определим по формуле Стэрджеса (которая для многих задач дает оптимальную длину интервала, позволяющую выявить характерные черты варьирования наблюдений):
(год).
Сами интервалы будут такими: (x min; x min+ h), (x min+ h; x min+2 h), …; построение интервалов заканчивают как только конец очередного интервала не станет равным или большим x max. В условиях задачи интервалы будут такими: (0; 1), (1; 2), …, (7; 8). Результат работы средства «Гистограмма» при введении в качестве карманов чисел 1, 2, 3, …, 8 приведена на рис.3.
| Карман | Частота | Интегральный % |
| 40,00% | ||
| 66,00% | ||
| 81,00% | ||
| 90,00% | ||
| 95,00% | ||
| 98,00% | ||
| 99,00% | ||
| 100,00% | ||
| Еще | 100,00% |
Рис.3. Результат работы средства Гистограмма
Судя по результатам у 40 рецидивистов промежуток времени X между преступлениями не превысил 1 года (X ≤1), у 26 рецидивистов: 1< X ≤2, у 15 рецидивистов: 2< X ≤3 и т.д.
В ряде задач статистические данные задаются в группированном виде. Формулы расчета выборочных характеристик: , , 
по данным, сгруппированным в статистический ряд, таковы:
где l – число групп ряда,
xi – вариант (центр интервала для интервального ряда),
mi – частота варианта (интервальная частота).
Вычислим среднюю продолжительность времени пребывания на свободе и среднее квадратическое отклонение времени. Результаты группировки, приведенные на рис.3, запишем в следующую таблицу:
| Интервал | 0..1 | 1..2 | 2..3 | 3..4 | 4..5 | 5..6 | 6..7 | 7..8 | |
| Число повторных судимостей (xi) | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | Итого |
| Количество человек (mi) | |||||||||
Опытная вероятность ( )
| 0,4 | 0,26 | 0,15 | 0,09 | 0,05 | 0,03 | 0,01 | 0,01 | |
| Экспоненциальная вероятность (pi) | 0,419 | 0,241 | 0,139 | 0,080 | 0,046 | 0,026 | 0,015 | 0,009 |
= (0,5*40+…+7,5*1)/100=1,81 (года),
(года).
Обратим внимание на то, что ≈ - это свойственно распределениям, построенным по наблюдениям «экспоненциальной» СВ – это непрерывная СВ X, вероятность попадания которой в малый интервал длиной h с центром в токе x рассчитывается так:
|
|
|
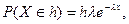где 
.
Заменив генеральное среднее MX на выборочное среднее =1,81, рассчитаем экспоненциальные вероятности попадания времени пребывания рецидивиста на свободе в соответствующие интервалы; они практически не отличаются от опытных вероятностей.
|
|
|
