Часть 2. Сравнение характеристик двух генеральных совокупностей

 

Допустим, что требуется на основании выборочных обследований сравнить два города по среднему возрасту и «вариабельности» (дисперсии) возраста гражданина, впервые нарушившего уголовное законодательство (или сравнить названные характеристики в одном городе до и после проведения соответствующих профилактических мероприятий). Введем обозначения:

X, MX, DX — возраст случайно выбранного нарушителя, средний возраст и дисперсия возраста нарушителя в первом городе соответственно;

Y, MY, DY — аналогичные характеристики для второго города.

Не имея возможности собрать сведения о возрасте всех нарушителей городов, а располагая лишь выборочными обследованиями: в первом городе собраны данные о возрасте n_X нарушителей, а во втором - n _Y, требуется проверить гипотезы Н₀: MX = MY и Н₀: DX = DY о том, что средний возраст нарушителя в городах одинаков и вариабельность (дисперсия) возраста одинакова.

Алгоритмы проверки гипотез Н₀: MX = MY и Н₀: DX = DY реализуются с помощью надстроек Excel «Двухвыборочный F -тест для дисперсий», «Парный двухвыборочный t -тест для средних», «Двухвыборочный t -тест с одинаковыми дисперсиями», «Двухвыборочный t -тест с различными дисперсиями», «Двухвыборочный z -тест для средних». Эти алгоритмы предполагают, что:

· n_X наблюдений СВ X (n_Y наблюдений СВ Y) проведены в типичных условиях;

· все n _X + n _Y наблюдений независимы;

· СВ Х (СВ Y) — нормально распределенная СВ.

«Двухвыборочный F-тест для дисперсий» используется для проверки гипотезы
Н₀: DX = DY (генеральные дисперсии одинаковы).

Исходные данные - введенные в рабочий лист наблюдения переменной 1 (СВ X) и наблюдения переменной 2 (СВ Y), а также уровень значимости α - вероятность отвергнуть верную гипотезу Н₀. По этим данным программа рассчитывает: средние и , дисперсии и и ряд других величин, необходимых для проверки гипотезы Н₀: DX = DY. Среди этих величин: dƒ — число степеней свободы, которое равно: n _X - 1 для переменной 1 и n _Y - 1 для переменной 2; ; вероятность «P одностороннее», называемая «рассчитанным уровнем значимости»: если «Р одностороннее»>α, гипотезу Н₀: DX - DY принимают; если «Р одностороннее»<α, то Н₀ не принимают; принимают альтернативную гипотезу Н₁, которая может быть двух видов:

Н₁: DX > DY, если > , и Н₁: DX < DY, если < .

При альтернативе Н₁: DX ≠ DY в диалоговое окно следует вместо α ввести α/2; если «p одностороннее» > α/2, принимают Н₀, в противном — Н₁.

 

ПРИМЕР 3.

Выборочные данные о возрасте (полное число лет) граждан, впервые совершивших уголовные преступления, таковы: 15, 17, 15, 21, 21, 18, 20 — в первом микрорайоне; 25, 16, 19, 24, 19, 20, 21, 23, 23 — во втором.

 

	Выборка
n	x1	x2

 

Результат программы «Двухвыборочный F -тест для дисперсий» при α = 0,05 приведен в таблице:

 

Двухвыборочный F-тест для дисперсии
	Переменная 1	Переменная 2
Среднее	18,143	21,111
Дисперсия	6,810	8,361
Наблюдения	7,000	9,000
df	6,000	8,000
F	0,814
P(F<=f) одностороннее	0,413
F критическое одностороннее	0,241

 

Вероятность «Р одностороннее» = 0,413 > α, поэтому гипотезу Н₀: DX = DY (при альтернативе Н₁: DX < DY, ведь дисперсия первой выборки меньше дисперсии второй выборки) принимаем: генеральная «вариабельность» возраста нарушителя в обоих микрорайонах одинакова, или различие выборочных дисперсий = 6,81 и = 8,361 незначимо, несущественно, связано со случайными ошибками выборки.

Программы «Парный двухвыборочный t -тест для средних», «Двухвыборочный t -тест с одинаковыми дисперсиями», «Двухвыборочный t -тест с различными дисперсиями», «Двухвыборочный z -тест для средних» используются для проверки гипотезы Н₀: MX - MY = а (разность генеральных средних равна числу а). Число а названо гипотетической разностью средних; по умолчанию а = 0 и тогда проверяемая гипотеза Н₀: MX = MY.

«Двухвыборочный t-mecm с одинаковыми дисперсиями» используется для проверки гипотезы только в том случае, когда есть основание считать равными генеральные дисперсии, DX = DY, хотя числовые значения этих дисперсий и неизвестны.

В качестве альтернативы к гипотезе Н₀: MX - MY = а при а = 0 может быть:

Н₁: MX > MY; Н₁: MX < MY; Н₁: MX ≠ MY.

Исходные данные программы - наблюдения величин X и Y и вероятность α.

По данным примера была принята гипотеза Н₀: DX = DY (принятие Н₀ служит основанием считать дисперсии равными, но не означает, что равенство дисперсий – абсолютная истина).

Результат программы «Двухвыборочный t-mecm с одинаковыми дисперсиями» при
α = 0,05 и «гипотетической разности средних» приведен в таблице:

 

Двухвыборочный t-тест с одинаковыми дисперсиями
	Переменная 1	Переменная 2
Среднее	18,143	21,111
Дисперсия	6,810	8,361
Наблюдения	7,000	9,000
Объединенная дисперсия	7,696
Гипотетическая разность средних	0,000
df	14,000
t-статистика	-2,123
P(T<=t) одностороннее	0,026
t критическое одностороннее	1,761
P(T<=t) двухстороннее	0,052
t критическое двухстороннее	2,145

 

В таблице «Объединенная дисперсия» - это оценка генеральной дисперсии обеих совокупностей, равная:

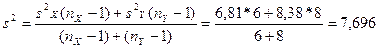; число степеней свободы

dƒ = n _X + n _Y – 2 = 14, статистика .

Альтернативой гипотезе Н₀: MX = MY (средний возраст преступника для микрорайонов одинаков) может быть:

· гипотеза Н₁: MX < MY (ведь =18,143 < =21,111); в этом случае Н₀ принимают, если рассчитанный «Односторонний уровень значимости», или вероятность «P одностороннее» > α, в противном – принимают Н₁ («P одностороннее» = 0,026 < α = 0,05, поэтому принимаем Н₁);

· гипотеза Н₁: MX ≠ MY; в этом случае Н₀ принимают, если «P двухстороннее» > α, в противном случае принимают Н₁ («P двухстороннее» = 0,052 > α = 0,05, принимаем гипотезу Н₀).

Пример показывает, что при неизменной вероятности α отвергнуть верную гипотезу Н₀ ответ на вопрос о том, принять или не принять гипотезу Н₀, зависит и от вида альтернативы Н₁.

«Парный двухвыборочный t-тест для средних» используется для проверки гипотезы Н₀: MX - MY = а, когда СВ X и СВ Y одноименные и наблюдаются «в паре»; в этом случае число n_X наблюдений СВ X равно числу n_Y наблюдений СВ Y, n _X = n _Y.

«Двухвыборочный t-тест с различными дисперсиями» используется для проверки гипотезы Н₀: MX - MY = а, когда есть основание считать генеральные дисперсии неравными: DX ≠ DY, хотя числовые значения этих дисперсий и неизвестны.

«Двухвыборочный z -тест для средних» используется для проверки гипотезы
Н₀: MX - MY = а, когда числовые значения дисперсий DX и DY известны.

В данных программах вопрос о том, принять или не принять гипотезу
Н₀: MX - MY = а решается также, как и в программе «Двухвыборочный t-mecm с одинаковыми дисперсиями».

 

Задания для самостоятельного выполнения:

Выполните самостоятельно действия, описанные в примерах 1-3. Результаты проделанной работы представьте в отчете по практической работе.

 

Контрольные вопросы:

1. Что понимается под статистической информацией?

2. Что такое средняя величина и каково ее значение в изучении материалов юридической статистики?

3. Для каких целей в статистике используются мода и медиана?

4. Назовите примеры задач правоприменительной деятельности, решаемых с использованием пакета «Анализ данных».

 

Литература:

1. Информатика и математика для юристов: учебник для студентов вузов, обучающихся по юридическим специальностям / [С.Я Казанцев и др.]; под ред. С.Я.Казанцева, Н.М.Дубининой. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2008. – 560с.

2. Абдулазар, Л. Лучшие методики применения Excel в бизнесе. – Пер. с англ. / Л. Абдулазар. – М.: Издательский дом «Вильямс», 2006. – 464 с.: ил.

3. Гмурман, В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов: 9-е изд., стер. / В.Е. Гмурман – М.: Высшая школа, 2003. – 479 с.

6. Минько, А.А. Сводные таблицы и диаграммы в Excel. Просто как дважды два /
А.А. Минько. – М.: Эксмо, 2008. – 208 с.: ил.

7. Макарова, Н.В. Статистика в Excel: Учеб. пособие / Н.В. Макарова, В.Я. Трофимец. – М.:Финансы и статистика, 2006. – 368 с.: ил.

 

 

⇐ Предыдущая21222324252627282930Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: