Взаимно простые многочлены.

Определение 1. Пусть f1(x), …, fk(x)Î P[x] и Е fi(x)¹ 0 (ненулевой набор многочленов). Если $ многочлен d(x) ÎP[x] такой, что:

1) старший коэффициент d(x) равен 1.

2) d(x) / fi(x) " i=1,…,k

3) если h(x) ÎP[x] обладает свойством h(x) / fi(x) "i, то h(x) / d(x), тогда d(x) называют НОД многочленов fi,…, fk

Обозначим НОД многочленов f1,…, fk через (f1,…, fk).

Выясним вопрос существования, однозначности и нахождения НОД.

Лемма 1: Пусть f1(x), …, fk(x)Î P[x],

М={ f1 j1+…+ fk jk | j1,…, j1 Î P[x] } — подмножество P[x]. f, g ÎM; u, v ÎP[x] Þ fu+gv ÎM.

< f=f1j1+…+ fkjk g = f₁ 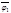+… +f_k fu+gv= f1(j1 u+ v)+…+ fk(jk u+ v) очевидно из М. >

Теорема 1. ( О существовании НОД)

Пусть f1(x), …, fk(x)Î P[x] — некоторые многочлены, среди них есть ненулевой. Тогда многочлен наименьшей степени из М, взятый со старшим коэффициентом 1, является наибольшим общим делителем этих многочленов.

< Сразу же заметим, что в М есть ненулевой многочлен — fi(x). Докажем, что все fi(x) r=1,…,k в множестве М. По определению М

f1 j1+…+ fk jk Î М, если j1=1; j2=…=jk=0; Þf1ÎM и т.д.

Очевидно также, что в М есть многочлены со старшим коэффициентом 1 (см. Лемму1):

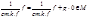
если f, g Î M.

Среди многочленов со старшим коэффициентом 1 выберем многочлен наименьшей степени. Обозначим его через d(x) и докажем, что это НОД. Во-первых, он со старшим коэффициентом 1 (мы его так выбрали).

Во-вторых, d(x) / fi(x) " i. (1)

Докажем (1). Допустим, что Ei d(x) ∤ fi(x), т.е d(x) не делит fi(x). Разделим с остатком fi (x) на d (x): fi(x)=d(x)q(x)+r(x). Выразим r(x):

r(x)= f_i(x)+d(x)(-q(x)) Î M.

Согласно Лемме о делении с остатком ст.r < ст.d(x).

Если старший коэффициент r(x) равен 1, то сразу же имеем противоречие с выбором d, если же старший коэффициент не равен 1, сделаем, чтобы он стал равен 1:

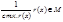(согласно Лемме 1)

Опять пришли к противоречию.

Докажем условие 3) в определении НОД.

Пусть h(x) | fi(x) " i d(x)= f1 j1+…+ fkjk ÎM Þ h(x) | d(x) (h(x) делит каждое из слагаемых, значит он делит сумму). >

Следствие (основное свойство НОД):

Наибольший общий делитель ненулевого набора многочленов f1, f2, …, fk представляется в виде: f1 y1,…,fn yk, где y1,…,ynÎP[x].

Это следует из способа доказательства теоремы о существовании НОД, ибо НОД –элемент из М.

Теорема 2.НОД определен однозначно.

<Пусть d₁ и d₂ — наибольшие общие делители многочленов f1,…,fk.

Тогда d₁ делит f1,…,fk, то есть d₁ │ f1,…,fk, отсюда следует, что d₁ / d₂ (по 3 свойству НОД). Аналогично d1 │ d2,значит можно записать d1 = a d2. А так как d1 и d2 со старшим коэффициентом 1,то в качестве a можно взять только единицу (a=1). Значит d1=d2,т.е. НОД определен однозначно. >

Лемма 2.Пусть f(x)=g(x)q(x)+r(x).Тогда наибольший общий делитель f и g равен наибольшему общему делителю g и r, т.е.: (f, g)=(g, r).

< Доказательство теоремы следует из определения. Пусть (f, g) = d1, (g, r) = d2.Тогда:

d1 │ f d2 │ g

Þ d1│ r Þ d1 │ d2 и d2 │ d1 Ü d2 │ f Ü

d1 │ g d2│ r

А значит: d1= d2. >

Теорема 3 (об отыскании НОД для двух многочленов).

Пусть f(x), g(x)ÎP[x], g(x)¹0. Тогда НОД многочленов f и g равен последнему, отличному от нуля, остатку в алгоритме Евклида для этих многочленов, взятому со старшим коэффициентом — единица. Если g | f, то НОД (f, g) равен .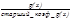

< Если g / f,то последнее утверждение в формулировке теоремы очевидно

Применяя Лемму 2 к системе равенство (4) предыдущего параграфа, получим,что

(f, g)=(g,r)=…=(r_k; r_k-1 )=

P.S. f=gq+r

g=rq₁+r₁

…………. система (4)

r_k-2=r_k-1+r_k

r_{k-1 =}r_kq_k+1+0. >

Замечание:

В теореме 3 содержится алгоритм практического отыскания НОД:

+ Ищем последний отличный от нуля остаток в алгоритме Евклида.

+ Делаем его со старшим коэффициентом единица,это и будет НОД.

Теорема 4.(f1,……….,fk)=((f1,……..,(f)(k-1)), fk), k≥2.

Эта теорема указывает путь, как процесс нахождения НОД для нескольких многочленов можно свести к нахождению НОД двух многочленов.

Определение.Многочлены f_{1,……….,}f_k называются взаимно простыми, если их НОД равен единице.

Теорема 5(критерий взаимной простоты).

Многочлены (f1,………., fk) взаимно простоты тогда и только тогда, когда $ u1,……,uk ÎP[x], такие что единица представляется в виде f1 u1 +……+fk uk.

<

Þ Имеем f1,……….,fk взаимно простые, то $ u1,……,uk ÎP[x], такие что f1u1 +……+fkuk=1. Это следует из основного свойства НОД.

Ü Пусть d(x)=(f1,……….,fk). Значит d(x) | 1 Þ d(x)=1 и значит многочлены взаимно простые.>

 

 

???. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ МНОГОЧЛЕНОВ (НОК).

Определение. Пусть f1(x),……,fk (x) Î P[x], fi¹0, "fi.Многочлен h(x) называют наименьшим общим кратным многочленов f1(x),……,fk (x), если:

1) fi (x) | h(x), т.е. h(x)-общее кратное многочленов;

2) "g(x), являющегося общим кратным, т.е. fi | g, "i, Þ h(x) | g(x). Обозначают НОК таким образом: [f1(x),……,fk (x)] = НОК (f1,……….,fk).

Свойства НОК:

1)[f1,f2] = — это дает правило вычисления НОК для двух многочленов;

2) [f1(x),……,fk (x)] = [f1(x),…fk-1],fk (x)] — это свойство сводит вычисление НОК для k многочленов к вычислению НОК для двух многочленов;

3) , ,

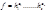[f, g]= , где 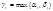, i=1,…..,s.

Докажем свойство 1):

< Обозначим [f1,f2] через m1, через m2, _{, .}

= = Þ Þ .

Если докажем, что ,т.е. m1 и m2 могут отличаться на постоянный множитель, то m₂ будет годиться в качестве НОК. >

Докажем свойство 3):

<

[f,g]= ,

то , где . >

43???.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: