Определение и примеры эвклидовых пространств.?

Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы:

(x, y) = (y, x),

(α ·x, y) = α ·(x, y),

(x + y, z) = (x, z) + (y, z),

(x, x) > 0 при x ≠ 0, (0, 0) = 0,

то в пространстве L определено скалярное произведение (x, y).

Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.

В линейном пространстве R₃ трёхмерных геометрических радиусов-векторов определёно скалярное произведение: (x, y) = |x|·|y|·cos{x,y}. Здесь cos{x,y} — косинус угла между векторами x и y.

Пример.

Легко проверить, что это для такого скалярного произведения справедливы аксиомы скалярного произведения:

(x, y) = |x|·|y|·cos{x,y} = |y|·|x|·cos{x,y}= (y, x),

(α ·x, y) = | α ·x|·|y|·cos{ α ·x,y} = |α|· sign(α)· |x|·|y|· cos{x,y} =α ·|x|·|y|· cos{x,y} = α·(x, y),

(x + y, z) = |x + y|·|z|·cos{x + y,z} = pr_z(x + y)·|z| = (pr_z(x)+pr_z(y))·|z| =

= (|x|·cos{x,z} + |y|·cos{x,z})·|z| =|x|·cos{x,z}·|z| + |y|·cos(x,z)·|z| = (x, z) + (y, z),

(x, x) = |x|·|x|·cos{x,x} = |x|·|x|·cos( 0 ) = |x|·|x| > 0 при x ≠ 0, (0, 0) = |0|·|0|·cos{0,0} = 0.

Линейное пространство R₃ трёхмерных геометрических радиусов-векторов с определённым в нём скалярным произведением (x, y) = |x|·|y|·cos{x,y} — евклидово пространство.

Определние вида кривой 2-го порядка по заданному уравнению. И ее построение.?

Общим уравнением второго порядка называется уравнение вида:

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0

где коэффициенты A,B,C одновременно не равны нулю.
Линии, определяемые такими уравнениями, называются кривыми второго порядка.
Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами.
Линии второго порядка, обладающие единственным центром, называются центральными.
Координаты центра S(x₀; y₀) линии определяются из системы:

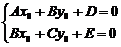
Обозначим через .
При Δ≠0 кривая второго порядка будет центральной.
Причем, при Δ>0 уравнение является уравнением эллиптического типа. Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (точка), либо мнимого эллипса (в этом случае уравнение не определяет на плоскости никакого геометрического образа).
При Δ<0 уравнение является уравнением гиперболического типа. Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную (пару пересекающихся прямых).
При Δ=0 линия второго порядка не является центральной. Такие уравнения называются уравнениями параболического типа и определяют на плоскости либо обыкновенную параболу, либо пару параллельных (или совпадающих) прямых, либо не определяют на плоскости никакого геометрического образа
Классификация кривых второго порядка:

· Эллипс

· Окружность

· Гипербола

· Парабола

Оптические свойства кривых второго порядка:

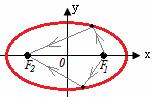
Для эллипса: лучи света, исходящие из одного фокуса эллипса, после зеркального отражения от эллипса проходят через второй фокус.

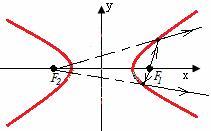
Для гиперболы: продолжение отраженного луча света, исходящего из одного фокуса гиперболы, попадает во второй фокус.

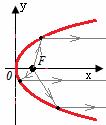
Для параболы: лучи света, исходящие из фокуса параболы, после зеркального отражения от нее образуют пучок лучей, параллельных ее фокальной оси.

Уравнение в полярных координатах.
Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы имеет вид:

где φ,ρ - полярные координаты произвольной точки линии, p –параметр, ε - эксцентриситет. При этом полярная система координат выбрана следующим образом: полюс находится в фокусе, полярная ось направлена в сторону, противоположную ближайшей к этому фокусу директрисы.
В частности, при ε=0, получим уравнение окружности в полярных координатах:
ρ=R

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: