 |
Спектральное представление детерминированного сигнала
|
|
|
|
Любой периодический сигнал можно рассматривать как бесконечную сумму гармоник. Удобно представить эту сумму в виде зависимости модуля амплитуды гармоники от частоты. Такое частотное распределение амплитуд гармоник, имеющее дискретный вид для периодического сигнала (рис.1.2), называется амплитудно-частотной характеристикой (АЧХ) спектра этого сигнала.
Для непериодического сигнала расстояние между спектральными линиями становится равным нулю, АЧХ имеет вид непрерывной функции (рис.1.3).
Каждая частотная составляющая периодического сигнала в общем случае имеет фазовый сдвиг, т. е. смещение начала гармоники относительно точки, принятой за нулевую. Это смещение выражается в угловой мере (радианах, градусах). Его можно оценивать фазо-частотной характеристикой (ФЧХ). Понятие ФЧХ распространяется и на непериодические сигналы.
Вся информация как о модуле амплитуды, так и о фазе частотных составляющих содержится в функции, называемой спектральной плотностью сигнала [1].
Рис. 1.2. Пример амплитудно-частотной характеристики периодического сигнала:
(А – модуль амплитуды гармоник, n - частота гармоник)
Рис. 1.3. Пример АЧХ апериодического сигнала
Спектральная плотность 
сигнала связана с сигналом E(t) прямым преобразованием Фурье:
| (1.1) |
и наоборот, сигнал E(t) может быть найден по его спектральной плотности обратным преобразованием Фурье:
| (1.2) |
По формуле Эйлера
| exp(± ix) = cos x ± i sin x. | (1.3) |
Используя формулу Эйлера (1.3), спектральную плотность , определяемую выражением (1.1), можно представить как алгебраическую сумму вида:
| = A (v) – iB (v),
| (1.4) |
где A (v) и B (v) – соответственно косинус- и синус-преобразования Фурье, рассчитываемые по формулам
|
|
|
| (1.5) | |
| (1.6) |
Спектральную плотность можно также выразить через две другие частотные характеристики: амплитудно-частотную S (v) и фазо-частотную ФЧХ q(v):
| = S (v)exp(i q(v)),
| (1.7) | |||
| где | 
| (1.8) | ||
| (1.9) | |||
Очевидно, что АЧХ S (v) является четной функцией, а ФЧХ q(v) – нечетной.
Сигнал E (t) можно найти, зная его АЧХ S (v) и ФЧХ q(v):
| (1.10) |
Четность АЧХ и нечетность ФЧХ позволяет упростить выражение (1.10) и привести его к виду:
| (1.11) |
Значение спектральной плотности и АЧХ S(v) на нулевой частоте есть интеграл вида
| (1.12) |
а ФЧХ q(v) обращается в нуль:
| q(0) = 0. | (1.13) |
Пример. Найдем АЧХ S (v) и ФЧХ q(v) сигнала E (t), представляющего собой прямоугольный импульс (рис.1.4).
Рис. 1.4. График прямоугольного импульса
Сначала вычислим синус- и косинус-преобразования Фурье A (v) и B (v), используя формулы (1.5) и (1.6). Бесконечные пределы в данном конкретном случае заменяем на – t э/2 и t э/2. Внутри этих пределов значение сигнала E (t) равно A. Выражение (1.6) в данном случае есть интеграл с симметричными пределами нечетной функции (сигнал E (t) – четная функция, синус – нечетная, их произведение – нечетная функция). Следовательно, в данном случае, как и для всех четных сигналов, синус-преобразование B (v) обращается в нуль. Расчет косинус-преобразования A (v) по формуле (1.5) приводит к интегралу вида
| (1.14) |
После интегрирования правой части выражения (1.14) получим:
 .
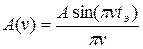| (1.15) |
Чтобы упростить формулу (1.15), используем функцию вида
 .
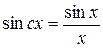| (1.16) |
Тогда выражение (1.15) примет вид:
| A (v) = At эsin c (π vt э). | (1.17) |
Так как в данном случае из-за четности сигнала B(v) = 0, то
| S (v) = A (v) = At эsin c (π vt э). | (1.18) |
|
|
|
График S (v) схематично приведен на рис. 1.5 и представляет собой четную функцию, осциллирующую относительно оси v с постоянным периодом и убывающей амплитудой. При нулевом значении v функция sin cx равна 1 (отношение величин при их стремлении к нулю заменяется отношением производных).
Рис.1.5. АЧХ прямоугольного импульса
ФЧХ сигнала q(v), вычисляемая по формуле (1.9), равна нулю, т. к. функция B (v) обратилась в нуль. ФЧХ равна нулю для всех четных сигналов.
|
|
|
