 |
Центральная предельная теорема для одинаково распределенных слагаемых
|
|
|
|
Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемыми на распределения образующих сумму случайных слагаемых. Здесь мы сформулируем и докажем одну из самых простых форм центральной предельной теоремы, относящуюся к случаю одинаково распределенных слагаемых.
Теорема. Если 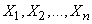 - независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием
- независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием  и дисперсией
и дисперсией  , то при неограниченном увеличении
, то при неограниченном увеличении  закон распределения суммы
закон распределения суммы
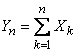 (13.8.1)
(13.8.1)
неограниченно приближается к нормальному.
Доказательство.
Проведем доказательство для случая непрерывных случайных величин 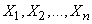 (для прерывных оно будет аналогичным).
(для прерывных оно будет аналогичным).
Согласно второму свойству характеристических функций, доказанному в предыдущем  ,характеристическая функция величины
,характеристическая функция величины  представляет собой произведение характеристических функций слагаемых. Случайные величины
представляет собой произведение характеристических функций слагаемых. Случайные величины 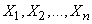 имеют один и тот же закон распределения с плотностью
имеют один и тот же закон распределения с плотностью 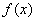 и, следовательно, одну и ту же характеристическую функцию
и, следовательно, одну и ту же характеристическую функцию
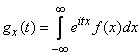 . (13.8.2)
. (13.8.2)
Следовательно, характеристическая функция случайной величины  будет
будет
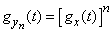 . (13.8.3)
. (13.8.3)
Исследуем более подробно функцию 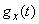 . Представим ее в окрестности точки
. Представим ее в окрестности точки  по формуле Маклорена с тремя членами:
по формуле Маклорена с тремя членами:
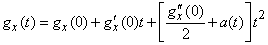 , (13.8.4)
, (13.8.4)
где  при
при  .
.
Найдем величины  ,
, 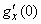 ,
,  . Полагая в формуле (13.8.2)
. Полагая в формуле (13.8.2)  имеем:
имеем:
 . (13.8.5)
. (13.8.5)
Продифференцируем (13.8.2) по  :
:
 . (13.8.6)
. (13.8.6)
Полагая в (13.8.6)  , получим:
, получим:
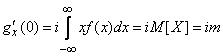 . (13.8.7)
. (13.8.7)
Очевидно, не ограничивая общности, можно положить  (для этого достаточно перенести начало отсчета в точку
(для этого достаточно перенести начало отсчета в точку  ). Тогда
). Тогда
 .
.
Продифференцируем (13.8.6) еще раз:
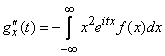 ,
,
отсюда
 . (13.8.8)
. (13.8.8)
При  интеграл в выражении (13.8.8) есть не что иное, как дисперсия величины
интеграл в выражении (13.8.8) есть не что иное, как дисперсия величины  с плотностью
с плотностью 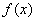 , следовательно
, следовательно
 . (13.8.9)
. (13.8.9)
Подставляя в (13.8.4)  ,
,  и
и  , получим:
, получим:
|
|
|
 . (13.8.10)
. (13.8.10)
Обратимся к случайной величине  . Мы хотим доказать, что ее закон распределения при увеличении
. Мы хотим доказать, что ее закон распределения при увеличении  приближается к нормальному. Для этого перейдем от величины
приближается к нормальному. Для этого перейдем от величины  к другой («нормированной») случайной величине
к другой («нормированной») случайной величине
 . (13.8.11)
. (13.8.11)
Эта величина удобна тем, что ее дисперсия не зависит от  и равна единице при любом
и равна единице при любом  . В этом нетрудно убедиться, рассматривая величину
. В этом нетрудно убедиться, рассматривая величину  как линейную функцию независимых случайных величин
как линейную функцию независимых случайных величин 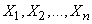 , каждая из которых имеет дисперсию
, каждая из которых имеет дисперсию  . Если мы докажем, что закон распределения величины
. Если мы докажем, что закон распределения величины  приближается к нормальному, то, очевидно, это будет справедливо и для величины
приближается к нормальному, то, очевидно, это будет справедливо и для величины  , связанной с
, связанной с  линейной зависимостью (13.8.11).
линейной зависимостью (13.8.11).
Вместо того чтобы доказывать, что закон распределения величины  при увеличении
при увеличении  приближается к нормальному, покажем, что ее характеристическая функция приближается к характеристической функции нормального закона.
приближается к нормальному, покажем, что ее характеристическая функция приближается к характеристической функции нормального закона.
Найдем характеристическую функцию величины  . Из соотношения (13.8.11), согласно первому свойству характеристических функций (13.7.8), получим
. Из соотношения (13.8.11), согласно первому свойству характеристических функций (13.7.8), получим
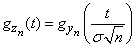 , (13.8.12)
, (13.8.12)
где  - характеристическая функция случайной величины
- характеристическая функция случайной величины  .
.
Из формул (13.8.12) и (13.8.3) получим
 (13.8.13)
(13.8.13)
или, пользуясь формулой (13.8.10),
 . (13.8.14)
. (13.8.14)
Прологарифмируем выражение (13.8.14):

 .
.
Введем обозначение
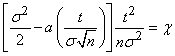 . (13.8.15)
. (13.8.15)
Тогда
 . (13.8.16)
. (13.8.16)
Будем неограниченно увеличивать  . При этом величина
. При этом величина  , согласно формуле (13.8.15), стремится к нулю. При значительном
, согласно формуле (13.8.15), стремится к нулю. При значительном  ее можно считать весьма малой. Разложим,
ее можно считать весьма малой. Разложим,  в ряд и ограничимся одним членом разложения (остальные при
в ряд и ограничимся одним членом разложения (остальные при  станут пренебрежимо малыми):
станут пренебрежимо малыми):
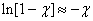 .
.
Тогда получим
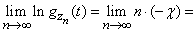
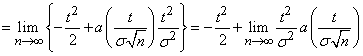 .
.
По определению функция 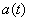 стремится к нулю при
стремится к нулю при  ; следовательно,
; следовательно,

и
 ,
,
откуда
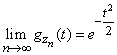 . (13.8.17)
. (13.8.17)
Это есть не что иное, как характеристическая функция нормального закона с параметрами  ,
,  (см. пример 2,
(см. пример 2,  13.7).
13.7).
Таким образом, доказано, что при увеличении  характеристическая функция случайной величины
характеристическая функция случайной величины  неограниченно приближается к характеристической функции нормального закона; отсюда заключаем что и закон распределения величины
неограниченно приближается к характеристической функции нормального закона; отсюда заключаем что и закон распределения величины  (а значит и величины
(а значит и величины  ) неограниченно приближается к нормальному закону. Теорема доказана.
) неограниченно приближается к нормальному закону. Теорема доказана.
|
|
|
Мы доказали центральную предельную теорему для частного, но важного случая одинаково распределенных слагаемых. Однако в достаточно широком классе условий она справедлива и для неодинаково распределенных слагаемых. Например, А. М. Ляпунов доказал центральную предельную теорему для следующих условий:
 , (13.8.18)
, (13.8.18)
где 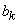 - третий абсолютный центральный момент величины
- третий абсолютный центральный момент величины  :
:
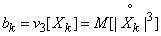
 .
.
 - дисперсия величины
- дисперсия величины  .
.
Наиболее общим (необходимым и достаточным) условием справедливости центральной предельной теоремыявляется условие Линдеберга: при любом 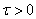
 ,
,
где  - математическое ожидание,
- математическое ожидание,  - плотность распределения случайной величины
- плотность распределения случайной величины  ,
,  .
.
|
|
|


