Сформулируйте основные свойства функции распределения случайного вектора (Х,У) и приведите примеры двумерной функции распределения.

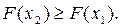
Следствие 1. Вероятность того, что непрерывная случайная величина X примет одно определённое значение, равна нулю, т.е. Р(Х=х¹)=0.

=F(b)-F(a)/

Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определённое значение, равна нулю, т.е. Р(Х=х¹)=0.

3) Если возможные значения случайной величины принадлежат интервалу (a;b), то 1) F(x)=0, х ≤ a, 2) F(x)=1, х ≥ b.

Следствие: Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливо равенство: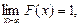

Свойства функции совместного распределения

Для простоты обозначений все дальнейшие рассуждения и формулировки приводятся в случае n=2 для случайного вектора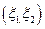

1)

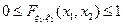
2) 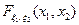не убывает по каждой координате вектора .

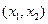3) Для любого i =1,2существует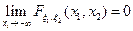
Для любого i =1,2существует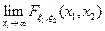
При этом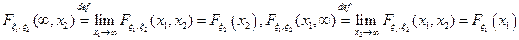

4) Функция 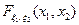по каждой координате вектора 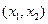непрерывна слева.

Функция, дающая для любой пары значений x, y вероятность того, что случайная величина Х будет меньше или равна x, а случайная величина Y меньше или равна y:
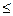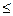F(x,y) = P(X x; Y y).
Примечание. Это понятие можно легко обобщить на большее число случайных величин.

Лапласа-Гаусса

95. Какой случайный вектор называется абсолютно непрерывным? Укажите основные свойства функции плотности распределения двумерного случайного вектора. Как можно найти непрерывную функцию плотности распределения двумерного случайного вектора, если известна его функция распределения? Укажите функцию плотности для равномерного распределения в круге радиуса R.

Случайный вектор называется абсолютно непрерывным, если существует 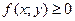- плотность распределения, такая, что:

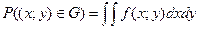
Свойства f(x;y):

1) f(x;y) – неотрицательная

2) dxdy=1

3) 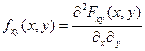В точке непрерывности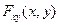

Если F(х;у) известна => 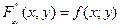- в точках непрерывности f(x,y).

Пример: Случ вектор (Х;У) равномерно распределен в круге радиуса R.

Найти функцию плотности.

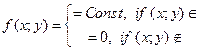кругу (if = если)

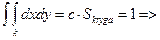
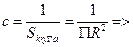
кругу

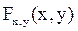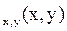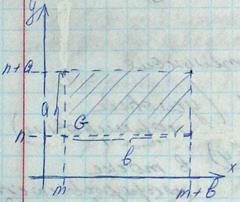
96. Как найти функцию распределения двумерного случайного вектора (X,Y), если известна функция плотности распределения f ? Укажите функцию распределения 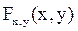для случайного вектора (X,Y), равномерно распределенного в прямоугольнике со сторонами a и b.

Ответ:

По св-ву плотности распределения следует:

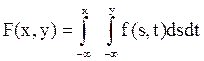
Равномерное распределение в прямоугольнике =>

F(x,y)=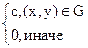

1 =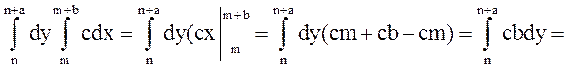

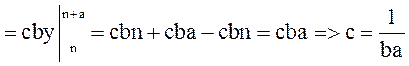
F(x,y)=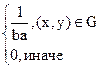

F(x,y)= 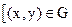т.к. иначе F(x,y), x>m+b, y>n+a, F(x,y)=1, x<m, y<n F(x,y=0]=

= =

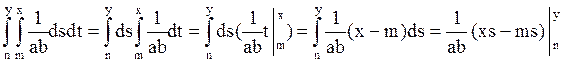= (x(y-n)-m(y-n))= (xy-xn-ym+mn).

97. Как найти функцию плотности f_x(x) и f_y(y) компонент Х и Y, если известна функция плотности f_X,Y(x,y) двумерного распределения (Х,Y)?

Для того чтобы найти функцию распределения компоненты при известной функции распределения двумерного распределения. Необходимо проинтегрировать данную функцию распределения по противоположной компоненте, т.е.

f_x(x)= 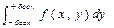и соответственно наоборот.

f(x,y)=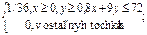

f_x(x)= 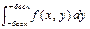= 1/36 =

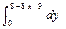98. Как можно найти функцию (,), f x y X Y плотности распределения случайного вектора (X, Y) с независимыми компонентами X и Y, если известны их плотности распределения f (x) X и f (y) Y? Будут ли независимыми компоненты случайного вектора (X, Y), равномерно распределенного в прямо-

угольнике a ≤ x ≤ b, c ≤ y ≤ d? Ответ обоснуйте.

По определению:

Компоненты Х и У абсолютно непрерывного случайного вектора называются независимыми, если

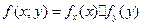
Пример: прямоугольник 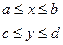, в котором вектор (х,у) равномерно распределен.

F(x;y)= 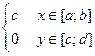иначе

При решении уравнения 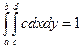найдем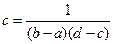

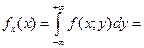
а)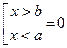

б)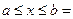

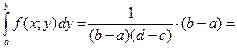
Аналогично для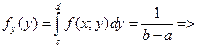

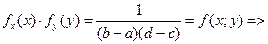
Компоненты Х и У - независимые

99. Как можно найти функцию распр F_x,y(x,y) случайного вектора (X,Y) с независимыми компонентами X и Y, если известны их ф-ии распр F_X(x) и F_Y(y)?

Если X и Y – независимые компоненты случ вектора (X,Y) и известна их ф-ия распр F_X(x) и F_Y(y), то его ф-ия распр F_x,y(x,y)= F_X(x)*F_Y(y). Обоснование.

Пусть A=(X<x), B=(Y<y), тогда P((XÎA)(YÎB))=F_x,y(x,y) и P(XÎA)*P(YÎB)=F_X(x)*F_Y(y), т.к. P((XÎA)(YÎB))=P(XÎA)*P(YÎB) (т.к. X и Y –независимые).

100. Как найти математическое ожидание функции 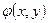, где Х,У – компоненты случайного вектора (Х,У)? Как определяются начальные k,l и центральные 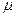k,l моменты случайного вектора (Х,У)?

Для математического ожидания функции ф(х, у) от компонент случайного вектора (X, Y) справедлива формула

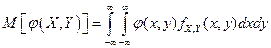
Мы видели, что в одномерном случае основные числовые характеристики случайной величины выражались через начальные и центральные моменты. Дадим аналогичное определение для случайного вектора.

Началъным моментом порядка (к, 1} называется математическое ожидание функции хку':

(1)

Центральным моментом порядка (к, Г) называется математическое ожидание функции (х-тх) \y-mY),где тх = М(Х), mY = M{Y):

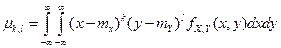
Числа к и l характеризуют порядок момента по отношению к каждой компоненте случайного вектора. Число r = к + l называют суммарным порядком момента. Соответственно суммарному порядку моменты можно разделить на моменты первого, второго и т.д. порядка. Мы рассмотрим более подробно моменты первого и второго порядка.

Первые начальные моменты - это нам уже знакомые математические ожидания случайных величин X и Y.

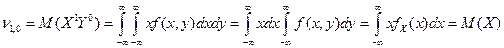
Аналогично,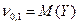

Точка с координатами (М(Х), M(Y)) характеризует центр системы случайных величин, вокруг которого происходит рассеивание возможных значений.

Кроме первых моментов широко применяют вторые централь­ные моменты, которые бывают трех типов. Два из них дают знакомые нам дисперсии компонент X и Y:

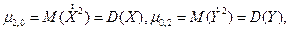
которые характеризуют рассеивание возможных значений случайных величин X и 7 вдоль осей х и у.

Особую роль в определении взаимодействия компонент играет второй смешанный центральный момент

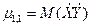
Мы уже рассматривали эту характеристику дискретных систем случайных величин, которую называли ковариацией. Она имеет важное значение и для непрерывных случайных векторов.