 |
Определение наблюдаемости. Анализ наблюдаемости системы.
|
|
|
|
Переходная матрица. Методы ее нахождения и ее свойства.
Переходная матрица 
позволяет отыскать решение 
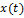в пространстве переменных состояний, начиная с некоторого значения 
до ∞. Она должна удовлетворять уравнениям:
, 
где E – единичная матрица.
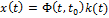
, сравниваем с 
=> 
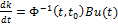
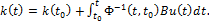
так как 
, получаем
. Обратная переходная матрица: 
. Решение системы в общем виде: 
.
Способы нахождения:
1) корни 
характеристического уравнения 
. Затем решаем n уравнений 
, откуда 
.
Переходная матрица: 
, где 
.
2) Для случая стационарных систем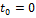 
, 
.
Применим преобразование Лапласа к диф. уравнению:
=> 
=> 
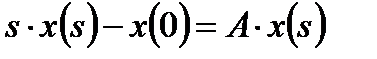
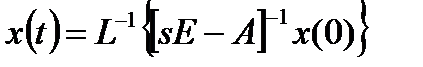
Откуда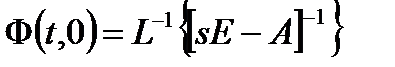 
3) 
, где 
– элемент переходной матрицы, представляет собой описание переходного процесса по i-ой координате вектора состояния при заданных единичных начальных условиях на j-ую координату вектора состояний при остальных координатах равных нулю.
Свойства переходной матрицы:
- Переходная матрица полностью определена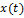
- Переходная матрица является невырожденной
3. Решение линейной нестационарной системы в пространстве состояний.
Переходная матрица t wx:val="Cambria Math"/><w:i/><w:sz w:val="20"/><w:sz-cs w:val="20"/></w:rPr><m:t>0</m:t></m:r></m:sub></m:sSub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="20"/><w:sz-cs w:val="20"/></w:rPr><m:t>)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> позволяет отыскать решение 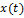в пространстве переменных состояний, начиная с некоторого значения до ∞. Она должна удовлетворять уравнениям:
|
|
|
, где E – единичная матрица.
Чтобы отыскать каким образом переходная матрица связана с 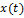, будем варьировать векторную переменную 
:
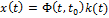
Дифференцируем систему: , сравниваем с уравнением в пространстве переменных состояний:
, домножим на обратную переходную матрицу 
:
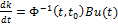
Интегрируем это выражение: 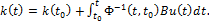Так как при 
выполняется второе уравнение переходной матрицы, то 
. Получаем уравнение: . Обратная переходная матрица: . Решение системы в общем виде: , где 
.
Решение линейной стационарной системы в пространстве состояний.
Для линейной стационарной системы переходная матрица примет вид для случая, если матрица A - диагональная. Проверяем является ли такая матрица переходной: 
, оба условия удовлетворены. В общем случае же 
, где , векторы собственных значений можно вычислить из , 
– матрица собственных значений вида 
. Собственные значения можно получить из уравнения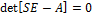 
Определение управляемости. Анализ управляемости системы.
Система называется полностью управляемой, если из произвольного начального состояния 
ее можно перевести в любое конечное состояние 
, при помощи входного сигнала, заданного на этом интервале времени (имея матрицы A и С). Заменим в пространстве переменных состояний 
и домножим 1ое уравнение на 
: 
, система приведена к диагональному виду, 
, получим n независимых уравнений.
Так как хотя бы один 
равен нулю, то система неуправляема. Для исследования управляемости нужно получить матрицу 
, и так как 
и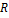 
невырожденная, то 
. Условием полной управляемости будет то, что ранг матрицы 
.
Определение наблюдаемости. Анализ наблюдаемости системы.
Система называется полностью наблюдаемой, если возможно определить начальное состояние , имея ее математическое описание (матрицы A и C) по выходному сигналу 
от начальных условий при 
. Заменим в пространстве переменных состояний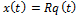 
и домножим первое уравнение на : , система приведена к диагональному виду, , получим n независимых уравн.
|
|
|
Так как хотя бы один 
равен нулю, то система не наблюдаема. Для исследования наблюдаемости нужно получить матрицу 
, и так как 
и 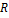невырожденная, то о наблюдаемости можно судить по прямоугольной матрице 
. Условием полной наблюдаемости будет то, что ранг матрицы 
.
|
|
|
