 |
Тест Голдфелда-Квандта
|
|
|
|
При малом объёме выборки для оценки гетероскедастичности используют тест Голдфелда-Квандта, разработанный в 1965г. М.Г. Голдфелд и Р.Э. Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора, остатки распределены нормально и не подвержены автокорреляции.
- упорядочить все n наблюдений по величине Х;
- вся упорядоченная выборка после этого разбивается на три подвыборки k, (k- 2 n), k;
- оцениваются отдельные регрессии для первой подвыборки(k первых наблюдений) и для третьей подвыборки (k последних наблюдений).
Замечание. Мощность критерия зависит от выбора значения k1 и k2 по отношению к n. Обычно выбирают k 1 = k 2 таким образом, чтобы вся совокупность разделилась на три равные части. Однако М.Г. Голдфелд и Р.Э. Квандт уточняют это правило и рекомендуют брать значения k 1= k 2= 11, если n = 30 и k 1= k 2= 22, если n = 60.
 Дисперсия суммы квадратов отклонений по первой и третьей выборке:
Дисперсия суммы квадратов отклонений по первой и третьей выборке:
Для сравнения соответствующих дисперсий строится следующая F-статистика:
 |
Здесь (k-m- 1 ) — число степеней свободы соответствующих выборочных дисперсий (m — количество объясняющих переменных в уравнении регрессии). По сделанным предположениям относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы ν1 = ν2 = k-m- 1.
Если Fнабл. ˃ Fкр. = Fɑ;ν1;ν2, то гипотеза об отсутствии гетероскедастичности отклоняется(здесь ɑ — выбранный уровень значимости).
Коэффициент ранговой корреляции Спирмена
Иногда встречаются случаи, когда необходимо установить тесноту связи между ординальными(порядковыми) переменными. В этом случае объекты анализа упорядочивают или ранжируют по степени выраженности измеряемых переменных. При этом каждому объекту присваивается определенный номер, называемый рангом. Если объекты ранжированы по двум признакам, то имеется возможность оценить тесноту связи между переменными, основываясь на рангах, т.е. тесноту ранговой корреляции.
|
|
|
 Коэффициент ранговой корреляции Спирмена находится по формуле:
Коэффициент ранговой корреляции Спирмена находится по формуле:
где di — разность рангов ri и si i -го объекта по переменным X и Y; n — число пар наблюдений.
Если ранги всех объектов равны (ri = si, i = 1,2,…, n), то ρ = 1, т.е. при полной прямой зависимости ρ = 1. При полной обратной связи, когда ранги объектов по двум переменным расположены в обратном порядке, можно показать, что ρ = –1. Во всех остальных случаях | ρ | ˂ 1.
При ранжировании иногда сталкиваются со случаями, когда невозможно найти существенные различия между объектами по величине проявления рассматриваемого признака: объекты, как говорят оказываются связанными. Связанным объектам приписывают одинаковые средние ранги, такие, чтобы сумма всех рангов оставалась такой же, как и при отсутствии связанных рангов. Например, если четыре объекта оказались равнозначными в отношении рассматриваемого признака и невозможно определить, какие из четырех рангов(4, 5, 6, 7) приписать этим объектам, то каждому объекту приписывается средний ранг, равный (4+5+6+7)/4 = 5,5.
 При проверке значимости ρ исходят из того, что в случае справедливости нулевой гипотезы об отсутствии корреляционной связи между переменными при n ≥ 10 статистика
При проверке значимости ρ исходят из того, что в случае справедливости нулевой гипотезы об отсутствии корреляционной связи между переменными при n ≥ 10 статистика
имеет t -распределение Стьюдента с (n - 2) степенями свободы. Поэтому ρ значим на уровне ɑ, если | t | ˃ t 1 - ɑ;n- 2, где t1-ɑ;n- 2 – табличное значение t -критерия Стьюдента, определенное на уровне значимости ɑ при числе степеней свободы (n - 2).
Пример1.
По результатам тестирования 10 студентов по двум дисциплинам A и В на основе набранных балов получены следующие ранги(табл). Вычислить коэффициент ранговой корреляции Спирмена и проверить его значимость на уровне ɑ =0,05.
|
|
|
Решение:
Разности рангов и их квадраты поместим в последних двух строках табл. 1.
Табл. 1.
| Ранги по дисциплинам | Результаты тестирования студентов | всего | ||||||||||
| А | ri | 7.5 | 7.5 | 7.5 | 7.5 | |||||||
| В | si | 2.5 | 2.5 | 9.5 | 9.5 | |||||||
| ri-si | -0.5 | -2 | 0.5 | -0.5 | -2 | -2 | 0.5 | - | ||||
| (ri-si)2 | 0.25 | 0.25 | 0.25 | 0.25 |
По формуле (*)
 |
Для проверки значимости ρ по формуле вычислим
 |
Найдем по таблице распределения Стьюдента t 0,95;8 = 2,31. Так как t ˃ t 0,95;8, то коэффициент ранговой корреляции ρ значим на 5%-ном уровне. Связь между оценками дисциплин достаточно тесная.
Использование коэффициента ранговой корреляции Спирмена для обнаружения гетероскедастичноси
При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличивается, либо уменьшаться с увеличением значения X. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений εi и значения xi случайного вектора X будут коррелированы. Значения xi и εi ранжируются(упорядочиваются по величинам). Затем используя формулу (*) определяется коэффициент ранговой корреляции, где di – разность между рангами xi и εi, i=1,2,…,n; n – число наблюдений.
Например, если x 20 является 25-м по величине среди всех наблюдений X; а ε 20– является 32-м, то di = 25 – 32 = – 7.
Если наблюдаемое значение t-статистики, вычисленное по формуле (**), превышает критическое tкр= t1-ɑ;n-2, то необходимо отклонить гипотезу о равенстве нулю коэффициенту корреляции ρ,а следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.
Если в модели регрессии больше чем одна объясняющая переменная, то проверка гипотезы может осуществляться с помощью t-статистики для каждой из них отдельно.
Пример 2.
Оценим регрессионную зависимость выпуска продукции обрабатывающей промышленности на душу населения y от валового внутреннего продукта на душу населения x в том же году для 17 стран.
|
|
|
Исходные данные представлены в табл. 2.
Наблюдения расположены в порядке возрастания независимой переменной x.
Пусть модель описывается выражением y =α+β x +ε.
По исходным данным с помощью МНК получена следующая регрессионная зависимость:
 |
(14,5) (0,6)
(в скобках указаны стандартные ошибки).
Табл. 2.
| n | y | x | n | y | x |
Для установления гетероскедастичности применим тест Спирмена.
Выдвигается нулевая гипотеза об отсутствии гетероскедастичности.
Отклонения от линии регрессии (остатки ε i) и данные по x в порядке возрастания приведены в табл. 3.
Табл. 3.
| X | ранг | | ε i | | ранг | D i | Di 2 | X | ранг | | ε i | | ранг | D i | Di 2 |
| 3,6 | -1 | 7,1 | |||||||||
| 3,3 | 2,8 | ||||||||||
| 15,2 | -6 | 1,2 | -3 | ||||||||
| 5,9 | 3,3 | -3 | |||||||||
| 4,2 | 4,5 | ||||||||||
| 11,4 | -1 | 5,0 | -2 | ||||||||
| 14,4 | -1 | 0,8 | |||||||||
| 9,8 | 8,7 | ||||||||||
| 7,9 | Итого |
 На основе этих данных вычислен коэффициент ранговой корреляции:
На основе этих данных вычислен коэффициент ранговой корреляции:
Для проверки значимости ρ по формуле вычислим:
 |
Это выше, чем tкр и, следовательно, нулевая гипотеза об отсутствии гетероскедастичности отклоняется.
Тест Уайта
Тест ранговой корреляции Спирмена и тест Гольдфельда-Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности.
|
|
|
При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений регрессоров, т.е.
s2 = fi (xi), 
Чаще всего функция f выбирается квадратичной, что соответствует тому, что средняя квадратичная ошибка регрессии зависит от наблюдаемых значений регрессоров приближенно линейно. Гомоскедастичной выборке соответствует случай f = const.
Идея теста Уайта заключается в оценке функции с помощью соответствующего уравнения регрессии для квадратов остатков:

 , где ui – случайный член.
, где ui – случайный член.
Гипотеза H0 об отсутствии гетероскедастичности (условие f = const) принимается в случае не значимости регрессии в целом.
a) Итак, сначала к исходной модели применяется обычный МНК;
b) Находятся остатки  ,
, 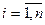 регрессии;
регрессии;
c) Осуществляется регрессия квадратов этих остатков  на все регрессоры x;
на все регрессоры x;
d) Осуществляется регрессия квадратов этих остатков  на квадраты регрессоров x 2;
на квадраты регрессоров x 2;
e) Осуществляется регрессия квадратов этих остатков  на попарные произведения регрессоров;
на попарные произведения регрессоров;
Для пунктов c) – e) считается F – статистика, если  где p – количество регрессоров, то гипотеза H0 об отсутствии гетероскедастичности отклоняется.
где p – количество регрессоров, то гипотеза H0 об отсутствии гетероскедастичности отклоняется.
Заметим, что на практике применение теста Уайта с включением и не включением попарных произведений дают, как правило, один и тот же результат.
Привлекательной чертой теста является его универсальность. Однако, если гипотеза H0 об отсутствии гетероскедастичности отклоняется, этот тест не дает указания на функциональную форму гетероскедастичности.
Ошибки в форме Уайта
Предположим, что Ω, матрица ковариаций вектора ошибок ε, диагональна, V( )=
)=  , где t= 1,…,n.
, где t= 1,…,n.
Элемент матрицы Ω - ( ) равен ковариации остатков для i -го и j -го значений результата:
) равен ковариации остатков для i -го и j -го значений результата:


 , если
, если 
Если 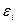 и
и  - ожидаемые значения.
- ожидаемые значения.
С точностью до  .
.
Пусть 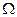 диагональна для любых i и j:
диагональна для любых i и j: 
Тогда:

В классе линейных несмещенных оценок вектора  для обобщенной регрессионной модели оценка
для обобщенной регрессионной модели оценка

имеет наименьшую ковариационную матрицу.
Подставим в эту формулу следующее выражение:

В результате получаем выражение вида:

 , где
, где 
Следовательно 
 Элемент матрицы Х – неслучайная величина.
Элемент матрицы Х – неслучайная величина.

Состоятельная оценка дисперсии коэффициентов регрессии в форме Уайта при наличии гетероскедастичности:
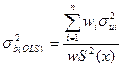 ;
;
 .
.
Дисперсия случайного члена:  .
.
С ростом выборки смещение оценки дисперсии уменьшается, следовательно t и F тесты асимптотически корректны.
Ошибки в форме Невье-Веста
Тест Невье-Веста используется для более сложных ситуаций. Одной из таких ситуаций может быть когда, ненулевые элементы в матрице ковариаций ошибок, стоят не только на главной диагонали, но и на соседних диагоналях, отстоящих от главной не более чем на L, т.е.:
|
|
|
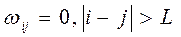
Невье и Вест показали, что оценка:


 Существует несколько способов выбора весовых коэффициентов
Существует несколько способов выбора весовых коэффициентов
1. Наиболее простым кажется взять:
Однако при таком выборе матрица (1) может оказаться не неотрицательно определённой.
 2. Бартлетт:
2. Бартлетт:
3. Парзен:
 |
В большинстве случаев использование весов Парзена предпочтительнее.
Тесты
1. Нарушением предпосылки МНК является случай _____ остатков.
a. нормального распределения;
b. случайного характера;
c. отсутствия автокорреляции;
d. гетероскедастичности.
2. Наличие гетероскедастичности остатков можно проверить с помощью…
a. теста Спирмена;
b. критерия Стьюдента;
c. теста Дарбина-Уотсона;
d. теста Фишера.
3. Гомоскедастичность остатков подразумевает…
a. максимальную дисперсию остатков при средних значениях фактора;
b. уменьшение дисперсии остатков с уменьшением значения фактора;
c. рост дисперсии остатков с увеличением значения фактора;
d. одинаковую дисперсию остатков при каждом значении фактора.
Литература
|
|
|


