 |
F(a)F(b)<0.
|
|
|
|
X3 – 0, 01·X2 – 0, 7044·X + 0, 139104 = 0
Замечание. Так как мы ищем корни многочлена третьей степени, то имеется не более трёх действительных корней.
Для нахождения корней их первоначально надо локализовать, т. е. найти интервалы, на которых корни существуют. Такими интервалами локализации корней могут служить промежутки, на концах которых функция имеет противоположные знаки. Для этого необходимо протабулировать значения функции и построить её график.
Например, протабулируем наш многочлен на интервале [-1; 1] с шагом 0, 2. С этой целью:
1) введем в ячейку А2 значение -1, а в ячейку А3 – значение -0. 8;
2) выберем диапазон А2: А3, расположиv указатель мыши на маркере автозаполнения этого диапазона и протянем его на диапазон А4: А12;
3) в ячейку В2 введем формулу:
=А2^3-0, 01*A2^2-0, 7044*A2+0, 139104
4) выберем ячейку В2. Расположим указатель мыши на маркере автозаполнения ячейки и протянем его вдоль диапазона В3: В12.

Рис. 4. 1. Локализация корней многочлена и диалоговое окно Подбор параметра
Из рис. 4. 1 видно, что многочлен меняет знак на интервалах [-1; -0, 8], [0, 2; 0, 4] и [0, 6; 0, 8], и поэтому на каждом из этих интервалов имеется свой корень. Так как многочлен третьей степени имеет не более трёх корней, то они все локализированы.
Прежде чем приступить к нахождению корней при помощи механизма Подбора параметра, необходимо выполнить некоторую подготовительную работу:
− следует установить точность, с которой ищется корень. Заметим, что корень при помощи Подбора параметра находится методом последовательных приближений. Для этого нужно выбрать команду Сервис – Параметры и на вкладке Вычисления задать относительную погрешность и предельное число итераций равным, например, 0, 00001 и 1000, соответственно;
|
|
|
− следует отвести на рабочем столе ячейку, например С2, под искомый корень. Эта ячейка будет играть двойную роль. До применения подбора параметра в ней находится начальное значение приближения к корню уравнения, а после применения – найденное приближение значение корня;
− корень при помощи Подбора параметра находим методом последовательных приближений. Поэтому в ячейку С2 надо ввести значение, являющееся приближением к искомому корню. В нашем случае, первым отрезком локализации корня является [-1; -0, 8]. Следовательно, за начальное приближение к корню разумно взять среднюю точку этого отрезка -0, 9;
− следует отвести ячейку, например D2, под функцию, для которой ведётся поиск корня, причём вместо неизвестной y этой функции должна указываться ссылка на ячейку, отведённую под корень. Таким образом, в ячейку D2 необходимо ввести формулу:
=С2^3 – 0, 01*С2^2 – 0, 7044*С2 + 0, 139104
Аналогично надо поступить с двумя другими искомыми корнями:
− отвести ячейку С3 под второй корень, ввести в неё начальное приближение 0, 3, а в ячейку D2 ввести следующую формулу
=С3^3-0, 01*C3^2 – 0, 7044*C2 + 0, 139104
− отвести ячейку С4 под третий корень, ввести в неё начальное приближение 0, 7, а в ячейку D4 ввести следующую формулу
=С4^3 – 0, 01*C4^2 – 0, 7044*C4 + 0, 139104
Теперь можно переходить к нахождению первого корня уравнения. Для этого следует выполнить последовательность действий:
1) выполнить команду Сервис – Подбор параметра. На экране отобразится диалоговое окно Подбор параметра;
2) в поле Установить в ячейке ввести ссылку на ячейку D2 (рис. 2. 19). В этом поле даётся ссылка на ячейку, в которой введена формула, вычисляющая значение левой части уравнения. Для нахождения корня с помощью подбора параметра уравнение надо представить в таком виде, чтобы его правая часть не содержала переменную;
|
|
|
3) в поле Значение ввести 0. Здесь указывается значение из правой части уравнения;
4) в поле Изменяя значение ячейки ввести С2. В данном поле задается ссылка на ячейку, отведённую под переменную;
5) нажать кнопку ОК.
На экране отображается окно Результат подбора пар аметра с результатами работы команды Подбор параметра. Кроме того, рассматриваемое средство помещает найденное приближенное значение корня в ячейку С2. В данном случае оно равно -0, 71999.
Аналогично в ячейках С3 и С4 находятся два оставшихся корня. Они равны 0, 21000 и 0, 71999 (рис. 4. 2).

Рис. 4. 2. Все найденные корни уравнения
Нахождение корней уравнения методом деления отрезка пополам
Хорошим упражнением по работе с Excel является программирование на рабочем листе алгоритма нахождения корня уравнения F(x)=0 методом деления отрезка пополам. Пусть непрерывная функция F(x) имеет значения разных знаков на концах отрезка [a; b], т. е.
F(a)F(b)< 0.
Тогда уравнение F(x)=0 имеет корень внутри этого отрезка. Отрезок [a; b] называется отрезком локализации корня.
Пусть с=(a+b)/2 – середина отрезка [a; b]. Если F(a)F(c)≤ 0, то корень находится на отрезке [a; c]; если F(a)F(c)> 0, то за новый отрезок локализации берём [c; b].
Отметим, что новый отрезок локализации корня в два раза меньше первоначального. Процесс деления отрезка для локализации корня продолжаем до сих пор, пока его длина не станет меньше å, точности нахождения корня. В этом случае любая точка отрезка локализации отличается от корня не более чем на å /2.
На рис. 4. 3 приведены результаты нахождения корня с точностью до 0, 001 методом деления отрезка пополам уравнения х2 – 2 = 0. За первоначальный отрезок локализации корня выбран [0; 2].
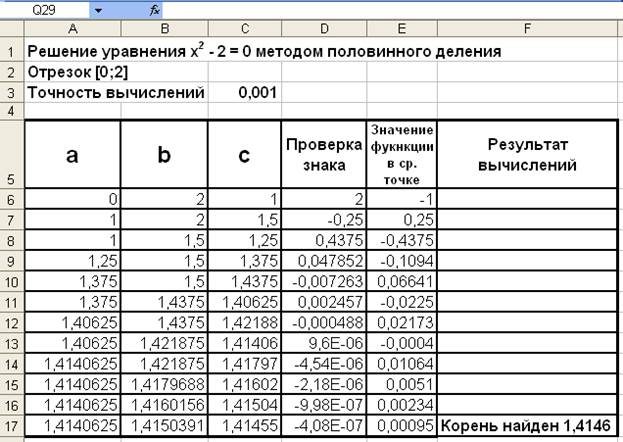
Рис. 4. 3. Нахождение корня уравнения методом деления отрезка пополам
Для реализации этого метода необходимо ввести в ячейки рабочего листа формулы либо значения, приведенные в табл. 4. 1.
Таблица 4. 1
Формулы для нахождения корней уравнения
| Ячейка | Формула либо значение |
| A6 | |
| B6 | |
| C6 | =(A6 + B6)/2 |
| D6 | =(A6^2 – 2)*(C6^2 – 2) |
| E6 | =C6^2 – 2 |
| F6 | =ЕСЛИ(В6 – А6< $C$3; “Корень найден и равен” & Текст(С6; “0, 0000”); ““) |
| A7 | =ЕСЛИ(D6< =0; A6; C6) |
| B7 | =ЕСЛИ(D6< =0; C6; B6) |
| C7 | =(A7+B7)/2 |
| D7 | =(A7^2-2)*(C7^2 – 2) |
| E7 | =C7^2 – 2 |
| F7 | =ЕСЛИ(В7 – А7< $C$3; “Корень найден и равен” & ТЕКСТ(С7; “0, 0000”); ””) |
|
|
|
Замечание. Функция ТЕКСТ – это функция из категории функций по работе с текстом. Она преобразует значение в текст в заданном числовом формате:
|
|
|


