 |
Проектирование бинарного канала передачи цифровой информации с циклическим кодом и частотной манипуляцией в системе Simulink
|
|
|
|
Задание на курсовой проект
Разработка и исследование помехоустойчивости цифрового канала с кодированием информации циклическим кодом и частотной манипуляцией при влиянии на канал связи гауссовской помехи
Исходные данные на проектирование:
Источник кодирования (датчик измерения) задан в виде аналоговой функции cos(cot)-0,3 sin(3 cot+pi/4), где со=0,2 рад/сек.
Канал измерения должен содержать (в обязательном порядке) следующие блоки:
предварительный непрерывный фильтр низкой частоты сигнала с датчика (сенсора) для уменьшения влияния частотного элайсинга (фильтр Баттерворта или эллиптический по усмотрению студента, расчет и моделирование проводится обоих фильтров),
АЦП для оцифровывания сигнала с фильтра ФНЧ,
преобразователь цифрового сигнала АЦП в последовательный битовый код в виде блоков (фреймов).
Для проектирования ФНЧ: допустимые пульсации в области пропускания Rp=3 дб, затухание в полосе задержания Rs= 60 дб, частота задержания Ws= 30 рад/сек, полоса пропускания Wp - определяется рабочей полосой пропускания датчика измерения.
Кодер, на который поступает от преобразователя последовательный битовый код в виде фреймов, кодирует этот сигнал циклическим кодом (n,k,t), где n-кодовое слово (информационное слово + корректирующее слово), k-корректирующее слово, t-число корректируемых ошибок в информационном слове.
Значения (n,k,t) по таблице кодов БЧХ задаются индивидуально для каждого студента. (n=7, k=4, t=l)
Сигнал с кодера поступает на цифровой частотный модулятор (манипулятор).
Сигнал с модулятора поступает в гауссовский канал связи. Соотношение сигнал/шум в канале связи варьируется в пределах snr=10:10 дб.
Сигнал связи поступает на цифровой частотный демодулятор (деманипулятор).
|
|
|
Сигнал с демодулятора поступает на декодер циклического кода (n,k,t).
В Пояснительной записке проекта представить:
Блок-схему цифрового канала.
Проектирование цифрового канала в Matlab с выводом зависимости вероятности ошибки в цифровом канале от соотношения сигнал/шум в гауссовском канале связи.
Моделирование поведения цифрового канала в Matlab.
Исходные данные для моделирования:
И=1000; %Количество передаваемых бит
М=2;
f0=l 180; % Несущая частота "нуля"
f1 =980; % Несущая частота "единицы"
Fs=9600; % Частота модулирующего сигнала Fd=300; % Частота символов
Fc=(f0+fl)/2; % Средняя несущая частота tone=f0-fl % Разность частот
m=4;
k=7; % Информационное слово
%t=2; % Количество корректируемых ошибок в информационном слове
n=2/m-1; % Кодовое слово (информационное слово + корректирующий код)
msg=randint(N,k); % Бинарная матрица распределения Гаусса от источника цифровой информации.
• Разработка модели цифрового канала в системе Simulink,
моделирование цифрового канала, представление в различных точках модели графиков поведения канала, оценка эффективности применения циклического кода и частотной манипуляции для повышения помехоустойчивости цифрового канала.
Сравнение на выходе частотного манипулятора (модулятора) и на выходе частотного деманипулятора (демодулятора) спектра цифровых сигналов (виртуальный спектрометр), их рассеяния (диаграмма рассеяния), времени оптимальной дискретизации (глазковая диаграмма).
Содержание
Задание на курсовой проект....................................................................... 2
Аннотация..................................................................................................... 5
Введение........................................................................................................ 6
Блок-схема..................................................................................................... 7
Литература................................................................................................. 21
Приложение А............................................................................................ 22
|
|
|
Приложение Б............................................................................................. 24
Приложение В............................................................................................ 27
Аннотация
Курсовая работа содержит 34 страницы, рисунков 24
Цель работы: Разработка и исследование помехоустойчивого цифрового канала с кодированием информации циклическим кодом и частотной манипуляцией при влиянии на канал связи гауссовской помехи
Введение
Работы в области информационно-измерительной техники и измерительных технологий позволили в последние годы создать новый раздел теории и практики измерений - виртуальные и интеллектуальные измерительные приборы и системы. Информационно-измерительная техника стала играть все более возрастающую роль в обществе.
Измерительные информационные системы предназначены, прежде всего, для обеспечения информацией потребителей. Вся человеческая деятельность, так или иначе, связана с управлением.
Измерительная информационная система- это совокупность функционально объединенных измерительных, вычислительных и других вспомогательных технических средств для получения измерительной информации, ее преобразования, обработки для предоставления потребителю в привычном для него виде.
Измерительная система - совокупность средств измерений, определенным образом соединенных между собой линиями связи, а также и других технических устройств (компонентов измерительной системы), образующих измерительные каналы. ИС реализует процесс измерений и обеспечивает автоматическое получение результатов измерений (выражаемых числом или кодом) в общем случае изменяющихся во времени и распределенных в пространстве величин, характеризующих определенные свойства (состояние) объекта измерений.
Измерительный канал измерительной системы - это конструктивно или функционально выделяемая часть ИС, выполняющая законченную функцию от восприятия измеряемой величины до получения результата ее измерений, выражаемого числом или соответствующим ему кодом, или до получения аналогового сигнала, один из параметров которого - функция измеряемой величины. Измерительный канал представляет собой последовательное соединение средств измерения (СИ), образующих ИС. Также ИК осуществляет преобразование измеряемой величины в сигнал, удобный для дальнейшего использования вне ИС, для передачи в цифровое или аналоговое вычислительное устройство, входящее в состав ИС. для совместного преобразования с другими величинами, для воздействия на исполнительные механизмы.
|
|
|
Блок схема

Исследование гауссовского бинарного канала передачи цифровой информации с циклическим кодом и частотной манипуляцией в системе Matlab и Simulimk.
N= 1000; % Количество передаваемых бит
М=2;
f0=1180; % Несущая частота "нуля"
f1=980; % Несущая частота "единицы"
Fs=9600; % Частота модулирующего сигнала
Fd=300; % Частота символов
Fc=(f0+fl)/2; % Средняя несущая частота
tone=f0-fl % Разнос частот
m=4;
k=7; % Информационное слово
%t=2; % Количество корректируемых ошибок в информационном слове
n=2/m-1; % Кодовое слово (информационное слово + корректирующий код)
msg=randint(N,k);% Бинарная матрица распределения Гаусса от источника цифровой информации
code = encode(msg,n,k,'cyclic/binary'); % Кодированние информационного слова
msgl=dmod(code,Fc,Fd,Fs,'fsk',M,tone);% Частотная манипуляция
snr=-10:10; % Соотношение сигнал/шум в Дб
for i=l:length(snr)
%msg=randint (1000,k);% Бинарная матрица распределения Гаусса от источника цифровой информации
%соdе = encode(msg,n,k,'cyclic/binary'); % Кодирование информационного слова
%h = modem. pammod('M', 1);
%msg 1 =dmod(code,Fc,Fd,Fs,'ask',M,tone); % Амплитудная манипуляция
%y = modulate(h,code);
msg2= awgn(msgl,snr(i),'measured'); % Гауссовский канал с шумом
msg3=ddemod(msg2,Fc,Fd,Fs,'fsk/noncoherence',M,tone); % Частотная деманипуляция
[newmsg,err,ccode,cerr] = decode(msg3,n,k,'cyclic/binary'); % Декодирование информационного слова
%hl = modem.pamdemod(msgl, 2);
%yl = demodulate(h 1, msgl);
%[numerrs(i), pcterrs(i)]=biterr(msg,newmsg); % Определение количества ошибок и вероятности их появления
[n_err, erc(i)]=symerr(msg,newmsg);
end
%numerrs;
%snr;
%pcterrs;
%figure(4);
%plot(numerrs,log(pcterrs)),grid; % График вероятности ошибок от соотношения сигнал/шум
figure(l);
semilogy(snr, ere), grid;
 |
Постройка графиков
Рисунок 1 с кодированием информационного слова

Рисунок 2 с кодированием и без кодирования
Например, при соотношении сигнал-шум «-4 ДБ» вероятность ошибок без кодирования - «10-2.5», а вероятность ошибок с кодированием - «10-1.5»
|
|
|
Проектирование бинарного канала передачи цифровой информации с циклическим кодом и частотной манипуляцией в системе Simulink
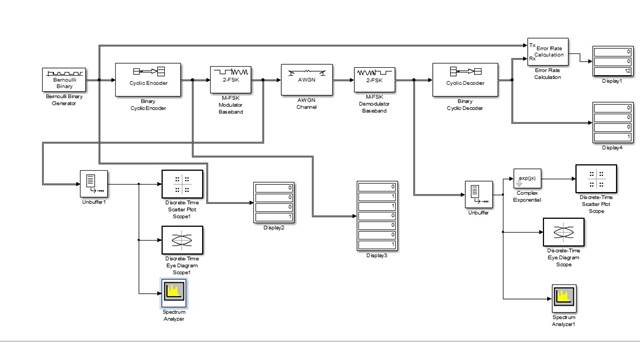

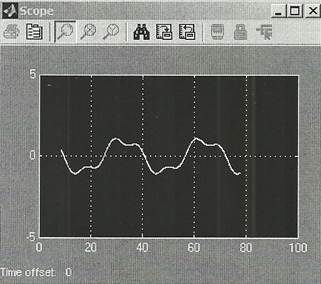
Рисунок 3 осциллограмма сложения после аналогового фильтра.

Рисунок 4 осциллограмма сложения sin cos
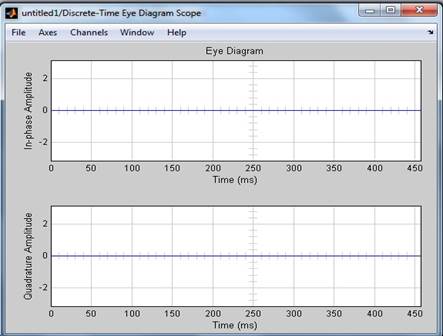
Рисунок 5 Глазковая диаграмма. Отношения времени к амплитуде, стоящая после модуляции и ещё не демодулированная.

Рисунок 6 Глазковая диаграмма. Отношения времени к амплитуде, стоящая после демодуляции.

Рисунок 7 Диаграмма рассеивания после демодуляции.
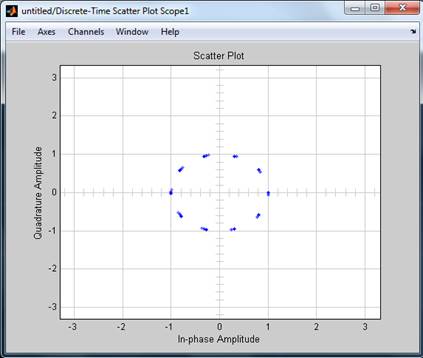
Рисунок 8 Диаграмма рассеивания после модуляции.
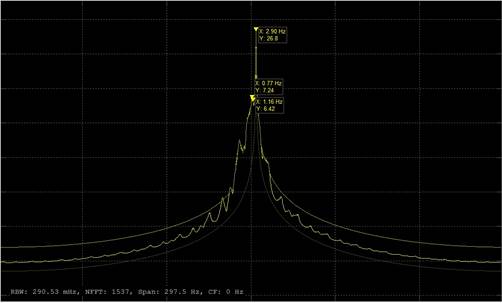
Рисунок 9 Спектр отношения частоты после демодуляции.

Рисунок 10 Спектр отношения частоты, стоящий перед декодировкой.
Библиографический список:
- Лекции профессора, д.т.н Симонов Евгений Николаевич.
- Электронная помощь программного пакета.
Приложение А
Отчет по лабораторной работе №1
1 Схема симметричного бинарного канала передачи цифровой информации.

|
2. Создать программу в Matlab по исследованию вероятности появления ошибки в цифровом сигнале после прохождения в симметричном канале.
%Исследование вероятности ошибки бинарного симметричного канала
for i=l:20
р (i)=0.02*i % Вероятность ошибки бинарного симметричного канала
z = randint(1,1000); % Бинарная матрица распределения Гаусса от источника цифровой информации
nz = bsc(z,р(i)); % Бинарный симметричный канал
[numerrs(i), peterrs(i)]=biterr(z,nz) % Определение количества ошибок и вероятности их появления
end
numerr;
peterr;
figure(1);
semilogy(numerrs,peterrs),grid; %График вероятности ошибоксимметричном канале от числа ошибок
3 Создать модель по исследованию бинарного симметричного канала в системе Simulink.
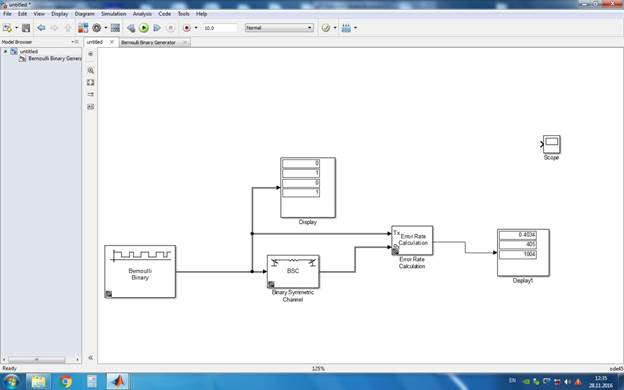
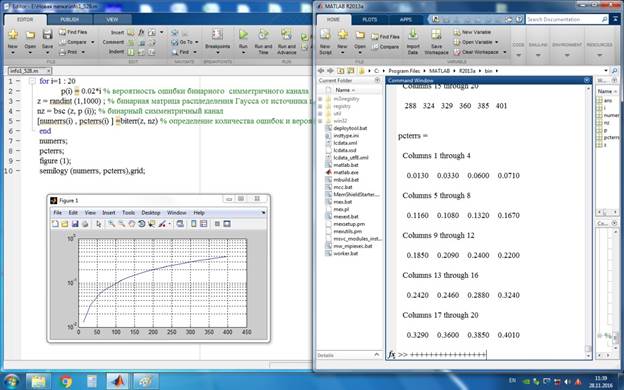
График 1. Вероятность и количество ошибок
Приложение Б
Отчет по лабораторной работе №2
Тема: Исследование кода Хемминга (7,4) для симметричного бинарного канала передачи цифровой информации в системе Matlab и Simulink.
1. Создать программу в Matlab по исследованию вероятности появления ошибки в цифровом сигнале после прохождения в симметричном канале при кодировании и декодировании кода Хемминга (7,4).
%Исследование кода Хемминга (4.7) для бинарного симметричного канала
for i=1:20
p(i)=0.02*i % Вероятность ошибки бинарного симметричного канала
n=7;
k=4;
msg=randint(1000,k); % Бинарная матрица распределения Гаусса от источника цифровой информации
code=encode(msg,n,k,'hammmg/binary');
msgl=bsc(code,p(i)); % Бинарный симметричный канал
msg2 = decode(msgl,n,k,'hamming/binary');
[numerrs(i), pcterrs(i)]=biterr(msg,msg2) % Определение количества ошибок и вероятности их появления
end
numerrs;
pcterrs;
figure(2);
semilogy(numerrs,pcterrs),grid; % График вероятности ошибок в симметричном канале от числа ошибок
|
|
|
2 Создать модель по исследованию кода Хемминга (7,4) для симметричного бинарного канала передачи цифровой информации в системе Simulink.
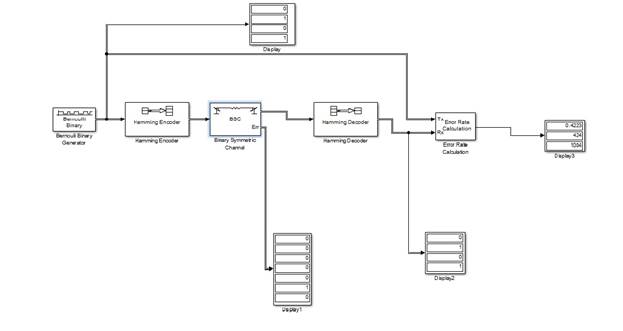
Изменяя вероятность ошибки бинарного канала в интервале P=0.02:0.4 определить количество ошибок на выходе декодера Хемминга;
Количество ошибок на выходе с применением декодера Хемминга
| При P=0.02 | 0.000996 | ||||
| При Р=0.05 | 0.0249 | ||||
| При Р=0.08 | 0.04582 | ||||
| При Р=0.16 | 0.1484 | ||||
| При Р=0.24 | 0.2879 | ||||
| При Р=0.3 | 0.3307 | ||||
| При Р=0.34 | 0.3775 | ||||
| При Р=0.4 | 0.4223 | ||||

График 2 Вероятность количества ошибок

Приложение В
|
|
|


