 |
Отчет по лабораторной работе № 3
|
|
|
|
Тема: Исследование циклического кода БЧХ (Боуза-Чаудхури-Хоквингема) высокой
корректирующей способности (n,k,t) для симметричного бинарного канала передачи
цифровой информации в системе Matlab и Simulink.
Создать программу в Matlab по исследованию вероятности появления ошибки в цифровом сигнале после прохождения в симметричном канале при кодировании и декодировании кодом БЧХ.
Значения n,k,t задаются по Таблице БЧХ-кодов.
‘’'«Исследование кода БЧХ высокой корректирующей способности для бинарного
Симметричного канала
ш=4;
к=7;%Информанионное слово
tr=2;%Ko;iячество корректируемых ошибок в информационном слове п=2Лш-1;% Кодовое слово (информационное слово+корректирующий код) for i=l:20
p(i)=0.02*i;%BepoHTHOCTb ошибки бинарного симметричного канала msg=randint(l000,к);% Бинарная матрица распределения Гаусса от источника цифровой информации
%msgl =gf(msg); % Бинарная матрица распределения Гаусса от источника цифровой информации в поле Галуа
%code = bchenc(msgl.n,k);
code = encode(msg,n,k,’bch');%Ko,aHpOBaHne информационного слова msg2=bsc(code,p(i));% Бинарный симметричный канал %noisycode=msg2 + randerr(1000,n,t);
% Decode the noisv code.
%[newmsg,errxcode] = bchdec(noisycode.n.k,'end');
[newmsg,err,ccode] = decode(msg2,n,k,'bch',t);%fleKojtHpoBaHHe кодового слова [numerrs(i), pcterrs(i)]=biterr(msg,newmsg); % Определение количества ошибок и вероятности их появления end
numerrs;
pcterrs;
figure(3);
semilogy(numerrs,pcterrs),grid; %График вероятности ошибок в симметричном канале от числа ошибок
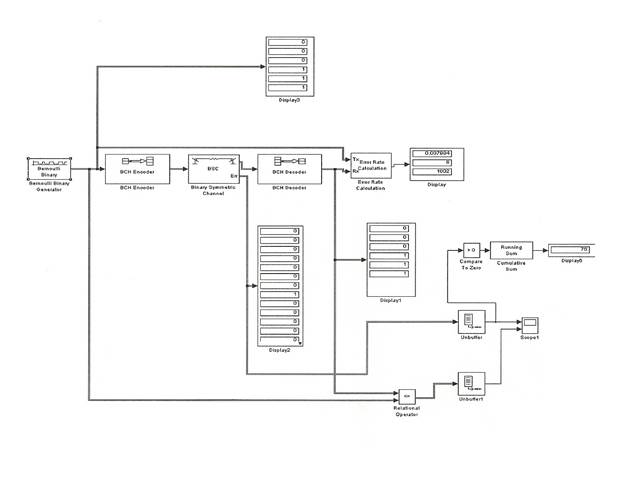
2. Создать модель по иследованию БЧХ-кода(7,4,1; 15,7,2; 31,11,5;63,30.6; 127,57,11) для симетричного бинарного канала передачи цифровой информации в системе Simulink.
 | |||
 |
 | |||||
 | |||||
 |
Приложение Г
Отчет по лабораторной работе №4
|
|
|
Тема: Исследование гауссовского бинарного канала передачи цифровой информации с циклическим кодом и частотной манипуляцией в системе Matlab и Simulink.
Создать программу в Matlab по исследованию вероятности появления ошибки в цифровом сигнале после прохождения в гауссовском канале при кодировании и декодировании циклическим кодом.
Значения n,k,t задаются по Таблице БЧХ-кодов.
%Исследование цифрового гауссовского канала с циклическим кодом и частотной манипуляцией
%Исследование цифрового гауссовского канала с циклическим кодом и частотной манипуляцией
N= 1000; % Количество передаваемых бит
М=2;
f0=1180; % Несущая частота "нуля"
f1=980; % Несущая частота "единицы"
Fs=9600; % Частота модулирующего сигнала
Fd=300; % Частота символов
Fc=(f0+fl)/2; % Средняя несущая частота
tone=f0-fl % Разнос частот
m=4;
k=7; % Информационное слово
%t=2; % Количество корректируемых ошибок в информационном слове
n=2/m-1; % Кодовое слово (информационное слово + корректирующий код)
msg=randint(N,k);% Бинарная матрица распределения Гаусса от источника цифровой информации
code = encode(msg,n,k,'cyclic/binary'); % Кодированние информационного слова
msgl=dmod(code,Fc,Fd,Fs,'fsk',M,tone);% Частотная манипуляция
snr=-10:10; % Соотношение сигнал/шум в Дб
for i=l:length(snr)
%msg=randint (1000,k);% Бинарная матрица распределения Гаусса от источника цифровой информации
%соdе = encode(msg,n,k,'cyclic/binary'); % Кодирование информационного слова
%h = modem. pammod('M', 1);
%msg 1 =dmod(code,Fc,Fd,Fs,'ask',M,tone); % Амплитудная манипуляция
%y = modulate(h,code);
msg2= awgn(msgl,snr(i),'measured'); % Гауссовский канал с шумом
msg3=ddemod(msg2,Fc,Fd,Fs,'fsk/noncoherence',M,tone); % Частотная деманипуляция
[newmsg,err,ccode,cerr] = decode(msg3,n,k,'cyclic/binary'); % Декодирование информационного слова
%hl = modem.pamdemod(msgl, 2);
%yl = demodulate(h 1, msgl);
%[numerrs(i), pcterrs(i)]=biterr(msg,newmsg); % Определение количества ошибок и вероятности их появления
[n_err, erc(i)]=symerr(msg,newmsg);
end
%numerrs;
%snr;
%pcterrs;
%figure(4);
%plot(numerrs,log(pcterrs)),grid; % График вероятности ошибок от соотношения сигнал/шум
|
|
|
figure(l);
semilogy(snr, ere), grid;
Провести анализ:
· Кодирующей способности циклического кода через сравнения вероятности появления ошибки на выходе информационного канала без кодирования-декодирования циклическим кодом и с кодом
· Помехоустойчивости гауссовского канала, варьируя соотношение сигнал/шум
2 Создать модель в системе Simulink о исследованию гауссовского канала передачи цифровой информации при кодировании и декодировании циклическим кодом.
|
|
|
