 |
Методические рекомендации для решения задач по общей тории статистики
|
|
|
|
Федеральное агентство по образованию
Министерства образования и науки Российской Федерации
Государственное образовательное учреждения высшего профессионального образования
Березниковский филиал
Пермского государственного университета
Кафедра экономики
СТАТИСТИКА
Учебно-методическое пособие
Березники, 2009 г.
Содержание
Предисловие
1. Методические рекомендации для решения задач по общей теории статистики
2. Задания к контрольной работе
Список рекомендуемой литературы
Предисловие
Изучение дисциплины «Статистика» предполагает формирование у слушателей теоретических основ и практических навыков в области познания социально-экономических явлений и процессов.
В результате изучения данной дисциплины студент должен усвоить систему обобщающих статистических показателей, овладеть методами обработки экономической информации, методологией комплексного анализа социально-экономических явлений на микро и макро уровнях.
При освоении дисциплины "Статистика" необходимо руководствоваться программами по:
1. Общей теории статистики;
2. Социально-экономической статистике.
Для более глубокого изучения студентам важнейших научно-методологических принципов статистики, приобретения практических навыков работы со статистическим материалом и методами его обработки и анализа, выработки умения правильно интерпретировать и грамотно формулировать аналитические выводы по рассчитанным статистическим показателям, необходимо выполнить контрольную работу.
Задания к контрольной работе составлены в восьми вариантах (1–4 задачи по разделу общей теории статистики, 5–8 - по социально-экономической статистике).
|
|
|
Выбор варианта производится в зависимости от начальной буквы фамилии слушателя.
| Начальная буква фамилии студента | Номер выполняемого варианта |
| А, И, Х, Э | первый |
| Б, Р, Ч | второй |
| В, П, Ц | третий |
| Г, О, Ф | четвертый |
| Д, Н, У | пятый |
| Е, М, С, Ш | шестой |
| Ж, Л, Т, Ю | седьмой |
| З, К, Щ, Я | восьмой |
Если в процессе выполнения контрольной работы возникнут трудности, то можно обратиться на кафедру экономики за консультацией (устной или письменной). В письменном запросе необходимо четко сформулировать непонятный вопрос и какой литературой студент при этом пользовался. При обращении на кафедру за устной консультацией необходимо показать преподавателю, что сделано по той или иной задаче и какие вопросы вызвали затруднение (непонятно изложено в литературе или в условии задачи).
При выполнении контрольной работы и ее оформлении необходимо руководствоваться следующими требованиями:
1. Контрольная работа должна быть выполнена в срок, установленный учебным планом.
2. В начале работы указывается номер выполняемого варианта.
3. Перед решением задачи должно быть полностью приведено ее условие.
4. Решение задач сопровождается описанием методологии расчета показателя или необходимыми формулами с пояснением условных обозначений в этих формулах.
Задачи, по которым будет приведена только арифметика, без пояснений и кратких выводов, или использованы не общепринятые сокращения (без пояснений), будут считаться нерешенными.
При решении задач необходимо проверять производимые расчеты, учитывая взаимосвязь вычисляемых показателей.
Расчеты относительных показателей нужно производить с точностью до 0,001, а проценты - до 0,1 (с учетом округлений).
5. Контрольная работа должна быть аккуратно оформлена, написана разборчиво (при плохом подчерке лучше отпечатать), страницы пронумерованы и иметь широкие поля для замечаний рецензента
|
|
|
Там, где решение задачи оформляется в табличной форме, таблицы должны быть построены и оформлены в соответствии с правилами, принятыми в статистике.
6. В конце работы приводится список использованной литературы (автор, название, место издания, издательство, год издания, глава, параграф, страница).
Студенты не получившие зачет по контрольной работе, не допускаются к экзамену.
Методические рекомендации для решения задач по общей тории статистики
Задача 1. Для решения этой задачи необходимо изучить темы общей теории статистики: ”Средние величины”, “Показатели вариации” и “Выборочное наблюдение”.
В условии задачи дается интервальный вариационный ряд распределения с открытыми интервалами. Чтобы определить среднее значение признака (пункт 1), нужно от интервального ряда перейти к дискретному, т.е. найти середину каждого интервала как полусумму нижней и верхней границ. При этом величина открытого интервала первой группы приравнивается к величине интервала второй группы, а величина открытого интервала последней группы - к величине интервала предпоследней группы.
Разновидностью средней являются мода и медиана (пункт 2). Эти величины также используются в качестве характеристик вариационного ряда.
Мода (Мо) – варианта, встречающаяся в ряду распределения чаще всего, т.е. варианта, которой соответствует наибольшая частота.
Для дискретного ряда распределения мода определяется наиболее просто: варианта, против которой расположена наибольшая частота, и будет модой.
В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Вычисление моды производится по следующей формуле:
где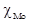 
- начало (нижняя граница) модального интервала; 
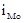- величина интервала; 
- частота модального интервала; 
- частота интервала, предшествующего модальному; 
- частота интервала, следующего за модальным.
Медиана 
– варианта, находящаяся в середине ранжированного ряда распределения. Для ее определения достаточно расположить в порядке возрастания или убывания все варианты. Серединная варианта и будет являться медианой. Расчет медианы для интервального ряда производится по формуле:
|
|
|
– начало (нижняя граница) медианного интервала; iMe – величина интервала; 
– сумма всех частот ряда; 
– сумма накопленных частот вариантов до медианного;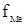 
–частота медианного интервала.
Для характеристики размеров колеблемости признаков в статистике используют ряд показателей (см. тему “ Показатели вариации”). В задаче 1 нужно исчислить дисперсию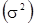 
, среднее квадратическое отклонение 
и коэффициент вариации 
(пункт 3):
; 
Чтобы рассчитать ошибки выборки (
) и возможные границы генеральной средней (
) и генеральной доли признака (
) нужно изучить тему “Выборочное наблюдение”.
Рассчитанная в пункте 1 данной задачи средняя является по условию задачи выборочной средней (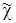
). Возможная граница генеральной средней (пункт 4) определяется по формуле:
,
где
предельная ошибка выборочной средней (для бесповторного отбора).
Возможная граница генеральной доли определяется по формуле:
где w – выборочная доля (удельный вес единиц в выборке, обладающих исследуемым признаком; w = m/n)
предельная ошибка выборочной доли (для бесповторного отбора).
Задача 2. Эта задача составлена на расчет и усвоение аналитических показателей динамических рядов. В условии задачи дан интервальный динамический ряд, поэтому средний уровень ряда может быть исчислен только по формуле средней арифметической простой:
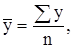
т.е. средний уровень ряда равен сумме уровней ряда, деленной на их число.
В зависимости от задачи исследования абсолютные приросты (снижения, 
), темпы роста (снижения, Т) и темпы прироста (снижения, 
) могут быть рассчитаны с переменной базой сравнения (цепные) и постоянной базой сравнения (базисные).
Абсолютные приросты:
цепные........................................ 
базисные...................................... 
Средний абсолютный прирост исчисляется двумя способами:
где 
– цепные абсолютные приросты; m – число цепных абсолютных приростов.
Темпы роста:
цепные........................................... 
|
|
|
базисные.......................................... 
Среднегодовой темп роста исчисляется по формуле средней геометрической двумя способами:
где 
- цепные коэффициенты роста; m - число этих коэффициентов.
Темпы прироста:
цепные................................... 
базисные.................................. 
или 
Среднегодовой темп прироста равен:
Абсолютное значение одного процента прироста (снижения) – это отношение абсолютного цепного прироста к соответствующему цепному темпу прироста, выраженному в процентах. Оно определяется по формуле:
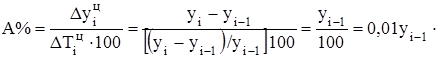
Задачи 3 и 4. Составлены по теме «Индексы».
Индексом в статистике называется относительный показатель, характеризующий соотношение по времени, по сравнению с планом или в пространстве уровней социально-экономических явлений.
При построении индексов рекомендуется придерживаться следующей символики: количество единиц данного вида произведенной или реализованной продукции обозначается – q; цена единицы изделия – p; себестоимость единицы изделия – z; трудоемкость единицы изделия – t; выработка продукции на одного работающего – w; удельный расход материалов (топлива) – m и т. д. Подстрочный значок 0 означает базисный, а 1 – отчетный периоды. Индивидуальный индекс обозначается латинской буквой i, а общий – I.
В первой части задачи 3 нужно рассчитать агрегатные индексы и сделать анализ влияния факторов по системе взаимосвязанных индексов.
Например, общие индексы необходимо исчислить по формулам:
1) общий индекс затрат на производство продукции:
,
2) общий агрегатный индекс себестоимости продукции:
3) общий агрегатный индекс физического объема производства продукции:
Эти индексы взаимосвязаны между собой:
Чтобы найти абсолютное изменение показателей, нужно от числителя соответствующего индекса вычесть его знаменатель. Так, абсолютный прирост (снижение) затрат на производство продукции равен:
,
в том числе: за счет изменения себестоимости продукции:
физического объема продукции:
Вторая часть задачи 3 составлена на расчет индекса переменного состава, индекса постоянного состава и индекса, измеряющего влияние изменения структуры на динамику среднего показателя (индекс структурных сдвигов).
Индекс переменного состава равен соотношению средних уровней изучаемого признака. Если, например, изучается динамика средней себестоимости одноименной продукции на двух и более заводах, то индекс себестоимости переменного состава исчисляется по формуле:
Изменение средней себестоимости единицы продукции может быть обусловлено изменением себестоимости единицы продукции на каждом заводе и изменением удельного веса производства продукции на каждом из анализируемых заводов.
|
|
|
Выявление влияния каждого из этих факторов на динамику средней себестоимости продукции можно осуществить при помощи расчета индекса себестоимости постоянного состава и индекса структурных сдвигов.
Индекс себестоимости постоянного (фиксированного) состава или индекс себестоимости в постоянной структуре, исчисляется по формуле:
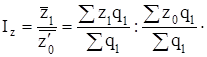
Этот индекс характеризует изменение средней себестоимости единицы продукции за счет изменения только уровней себестоимости на каждом из заводов.
Индекс структурных сдвигов рассчитывается по формуле:
стр.сдв.= 
Этот индекс характеризует изменение средней себестоимости единицы продукции за счет изменения только удельного веса количества произведенной продукции на отдельных заводах.
Индекс структурных сдвигов можно исчислить, используя взаимосвязи индексов, то есть:
стр..сдв 
.
Используя индексы средних величин, можно найти не только относительное влияние факторов, но и определить абсолютное изменение уровня среднего показателя в целом (
) и за счет каждого из факторов: за счет непосредственного изменения уровней осредняемого признака (
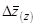) и за счет изменения структуры (
(стр. сдв.).). Для этого необходимо из числителя соответствующего индекса приведенной системы индексов вычесть его знаменатель.
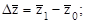
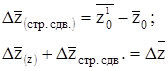
Задача 4. Составлена на расчет среднеарифметического илисреднегармонического индексов. Практическое их применение зависит от исходной статистической информации. Агрегатный индекс может быть преобразован в среднеарифметический или среднегармонический индекс, при этом должно быть соблюдено тождество между индексами.
Если у исходного агрегатного индекса реальная величина в числителе, то преобразуем его в среднегармоническую форму, если же реальная величина его у исходного агрегатного индекса в знаменателе, то преобразуем его в среднеарифметическую форму. Например, индекс цен:
В числителе индекса реальная величина - фактический товарооборот отчетного периода. Заменив po значением из индивидуального индекса:
, 
Это и есть среднегармонический индекс цен.
Агрегатный индекс физического объема товарооборота
,
исходя из правила, может быть будет преобразован в среднеарифметический индекс, т.е.
|
|
|
12 |
