Предметными результатами изучения предмета «Математика» являются следующие умения.

5 -й класс

Использовать при решении математических задач, их обосновании и проверке найденного решения знание:

- названий и последовательности чисел в натуральном ряду в пределах 1 000 000 (с какого числа начинается этот ряд, как образуется каждое следующее число в этом ряду);

- как образуется каждая следующая счётная единица;

- названия и последовательность разрядов в записи числа;

- названия и последовательность первых трёх классов;

- сколько разрядов содержится в каждом классе;

- соотношение между разрядами;

- сколько единиц каждого класса содержится в записи числа;

- как устроена позиционная десятичная система счисления;

- единицы измерения величин (длина, масса, время, площадь), соотношения между ними;

- функциональной связи между группами величин (цена, количество, стоимость; скорость, время, расстояние; производительность труда, время работы, работа).

Выполнять устные вычисления (в пределах 1 000 000) в случаях, сводимых к вычислениям в пределах 100, и письменные вычисления в остальных случаях; выполнять проверку правильности вычислений;

- выполнять умножение и деление с 1 000;

- вычислять значения числовых выражений, содержащих 3–4 действия со скобками и без них;

- раскладывать натуральное число на простые множители;

- находить наибольший общий делитель и наименьшее общее кратное нескольких чисел;

- решать простые и составные текстовые задачи;

- выписывать множество всевозможных результатов (исходов) простейших случайных экспериментов;

- находить вероятности простейших случайных событий;

- решать удобным для себя способом (в том числе и с помощью таблиц и графов) комбинаторные задачи: на перестановку из трёх элементов, правило произведения, установление числа пар на множестве из 3–5 элементов;

- решать удобным для себя способом (в том числе и с помощью таблиц и графов) логические задачи, содержащие не более трёх высказываний;

- читать информацию, записанную с помощью линейных, столбчатых и круговых диаграмм;

- строить простейшие линейные, столбчатые и круговые диаграммы;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

 

Й класс

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

- десятичных дробях и правилах действий с ними;

- отношениях и пропорциях; основном свойстве пропорции;

- прямой и обратной пропорциональных зависимостях и их свойствах;

- процентах;

- целых и дробных отрицательных числах; рациональных числах;

- правиле сравнения рациональных чисел;

- правилах выполнения операций над рациональными числами; свойствах операций.

– Сравнивать десятичные дроби;

- выполнять операции над десятичными дробями;

- преобразовывать десятичную дробь в обыкновенную и наоборот;

- округлять целые числа и десятичные дроби;

- находить приближённые значения величин с недостатком и избытком;

- выполнять приближённые вычисления и оценку числового выражения;

- делить число в данном отношении;

- находить неизвестный член пропорции;

- находить данное количество процентов от числа и число по известному количеству процентов от него;

- находить, сколько процентов одно число составляет от другого;

- увеличивать и уменьшать число на данное количество процентов;

- решать текстовые задачи на отношения, пропорции и проценты;

- сравнивать два рациональных числа;

- выполнять операции над рациональными числами, использовать свойства операций для упрощения вычислений;

- решать комбинаторные задачи с помощью правила умножения;

- находить вероятности простейших случайных событий;

- решать простейшие задачи на осевую и центральную симметрию;

- решать простейшие задачи на разрезание и составление геометрических фигур;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

 

Й класс.

Алгебра

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

- натуральных, целых, рациональных, иррациональных, действительных числах;

- степени с натуральными показателями и их свойствах;

- одночленах и правилах действий с ними;

- многочленах и правилах действий с ними;

- формулах сокращённого умножения;

- тождествах; методах доказательства тождеств;

- линейных уравнениях с одной неизвестной и методах их решения;

- системах двух линейных уравнений с двумя неизвестными и методах их решения.

- Выполнять действия с одночленами и многочленами;

- узнавать в выражениях формулы сокращённого умножения и применять их;

- раскладывать многочлены на множители;

- выполнять тождественные преобразования целых алгебраических выражений;

- доказывать простейшие тождества;

- находить число сочетаний и число размещений;

- решать линейные уравнения с одной неизвестной;

- решать системы двух линейных уравнений с двумя неизвестными методом подстановки и методом алгебраического сложения;

- решать текстовые задачи с помощью линейных уравнений и систем;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

Й класс.

Геометрия

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

- основных геометрических понятиях: точка, прямая, плоскость, луч, отрезок, ломаная, многоугольник;

- определении угла, биссектрисы угла, смежных и вертикальных углов;

- свойствах смежных и вертикальных углов;

- определении равенства геометрических фигур; признаках равенства треугольников;

- геометрических местах точек; биссектрисе угла и серединном перпендикуляре к отрезку как геометрических местах точек;

- определении параллельных прямых; признаках и свойствах параллельных прямых;

- аксиоме параллельности и её краткой истории;

- формуле суммы углов треугольника;

- определении и свойствах средней линии треугольника;

- теореме Фалеса.

- Применять свойства смежных и вертикальных углов при решении задач;

- находить в конкретных ситуациях равные треугольники и доказывать их равенство;

- устанавливать параллельность прямых и применять свойства параллельных прямых;

- применять теорему о сумме углов треугольника;

- использовать теорему о средней линии треугольника и теорему Фалеса при решении задач;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

 

Й класс.

Алгебра

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

- алгебраической дроби; основном свойстве дроби;

- правилах действий с алгебраическими дробями;

- степенях с целыми показателями и их свойствах;

- стандартном виде числа;

- функциях , , , их свойствах и графиках;

- понятии квадратного корня и арифметического квадратного корня;

- свойствах арифметических квадратных корней;

- функции , её свойствах и графике;

- формуле для корней квадратного уравнения;

- теореме Виета для приведённого и общего квадратного уравнения;

- основных методах решения целых рациональных уравнений: методе разложения на множители и методе замены неизвестной;

- методе решения дробных рациональных уравнений;

- основных методах решения систем рациональных уравнений.

- Сокращать алгебраические дроби;

- выполнять арифметические действия с алгебраическими дробями;

- использовать свойства степеней с целыми показателями при решении задач;

- записывать числа в стандартном виде;

- выполнять тождественные преобразования рациональных выражений;

- строить графики функций , , и использовать их свойства при решении задач;

- вычислять арифметические квадратные корни;

- применять свойства арифметических квадратных корней при решении задач;

- строить график функции и использовать его свойства при решении задач;

- решать квадратные уравнения;

- применять теорему Виета при решении задач;

- решать целые рациональные уравнения методом разложения на множители и методом замены неизвестной;

- решать дробные уравнения;

- решать системы рациональных уравнений;

- решать текстовые задачи с помощью квадратных и рациональных уравнений и их систем;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

 

Й класс.

Геометрия

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

- определении параллелограмма, ромба, прямоугольника, квадрата; их свойствах и признаках;

- определении трапеции; элементах трапеции; теореме о средней линии трапеции;

- определении окружности, круга и их элементов;

- теореме об измерении углов, связанных с окружностью;

- определении и свойствах касательных к окружности; теореме о равенстве двух касательных, проведённых из одной точки;

- определении вписанной и описанной окружностей, их свойствах;

- определении тригонометрические функции острого угла, основных соотношений между ними;

- приёмах решения прямоугольных треугольников;

- тригонометрических функциях углов от 0 до 180°;

- теореме косинусов и теореме синусов;

- приёмах решения произвольных треугольников;

- формулах для площади треугольника, параллелограмма, трапеции;

- теореме Пифагора.

- Применять признаки и свойства параллелограмма, ромба, прямоугольника, квадрата при решении задач;

- решать простейшие задачи на трапецию;

- находить градусную меру углов, связанных с окружностью; устанавливать их равенство;

- применять свойства касательных к окружности при решении задач;

- решать задачи на вписанную и описанную окружность;

- выполнять основные геометрические построения с помощью циркуля и линейки;

- находить значения тригонометрических функций острого угла через стороны прямоугольного треугольника;

- применять соотношения между тригонометрическими функциями при решении задач; в частности, по значению одной из функций находить значения всех остальных;

- решать прямоугольные треугольники;

- сводить работу с тригонометрическими функциями углов от 0 до 180° к случаю острых углов;

- применять теорему косинусов и теорему синусов при решении задач;

- решать произвольные треугольники;

- находить площади треугольников, параллелограммов, трапеций;

- применять теорему Пифагора при решении задач;

- находить простейшие геометрические вероятности;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

 

Й класс.

Алгебра

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

- свойствах числовых неравенств;

- методах решения линейных неравенств;

- свойствах квадратичной функции;

- методах решения квадратных неравенств;

- методе интервалов для решения рациональных неравенств;

- методах решения систем неравенств;

- свойствах и графике функции 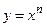при натуральном n;

- определении и свойствах корней степени n;

- степенях с рациональными показателями и их свойствах;

- определении и основных свойствах арифметической прогрессии; формуле для нахождения суммы её нескольких первых членов;

- определении и основных свойствах геометрической прогрессии; формуле для нахождения суммы её нескольких первых членов;

- формуле для суммы бесконечной геометрической прогрессии со знаменателем, меньшим по модулю единицы.

- Использовать свойства числовых неравенств для преобразования неравенств;

- доказывать простейшие неравенства;

- решать линейные неравенства;

- строить график квадратичной функции и использовать его при решении задач;

- решать квадратные неравенства;

- решать рациональные неравенства методом интервалов;

- решать системы неравенств;

- строить график функции 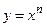при натуральном n и использовать его при решении задач;

- находить корни степени n;

- использовать свойства корней степени n при тождественных преобразованиях;

- находить значения степеней с рациональными показателями;

- решать основные задачи на арифметическую и геометрическую прогрессии;

- находить сумму бесконечной геометрической прогрессии со знаменателем, меньшим по модулю единицы;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

 

Й класс.

Геометрия

Использовать при решении математических задач, их обосновании и проверке найденного решения знание о:

- признаках подобия треугольников;

- теореме о пропорциональных отрезках;

- свойстве биссектрисы треугольника;

- пропорциональных отрезках в прямоугольном треугольнике;

- пропорциональных отрезках в круге;

- теореме об отношении площадей подобных многоугольников;

- свойствах правильных многоугольников; связи между стороной правильного многоугольника и радиусами вписанного и описанного кругов;

- определении длины окружности и формуле для её вычисления;

- формуле площади правильного многоугольника;

- определении площади круга и формуле для её вычисления; формуле для вычисления площадей частей круга;

- правиле нахождения суммы и разности векторов, произведения вектора на скаляр; свойства этих операций;

- определении координат вектора и методах их нахождения;

- правиле выполнений операций над векторами в координатной форме;

- определении скалярного произведения векторов и формуле для его нахождения;

- связи между координатами векторов и координатами точек;

- векторным и координатным методах решения геометрических задач.

- формулах объёма основных пространственных геометрических фигур: параллелепипеда, куба, шара, цилиндра, конуса.

- Применять признаки подобия треугольников при решении задач;

- решать простейшие задачи на пропорциональные отрезки;

- решать простейшие задачи на правильные многоугольники;

- находить длину окружности, площадь круга и его частей;

- выполнять операции над векторами в геометрической и координатной форме;

- находить скалярное произведение векторов и применять его для нахождения различных геометрических величин;

- решать геометрические задачи векторным и координатным методом;

- применять геометрические преобразования плоскости при решении геометрических задач;

- находить объёмы основных пространственных геометрических фигур: параллелепипеда, куба, шара, цилиндра, конуса;

- находить решения «жизненных» (компетентностных) задач, в которых используются математические средства;

- создавать продукт (результат проектной деятельности), для изучения и описания которого используются математические средства.

 

5. Содержание математического образования

 

Содержание математического образования в основной школе формируется на основе фундаментального ядра школь­ного математического образования. Оно в основной школе включает следующие разделы: арифметика, алгебра, функции, вероятность и статистика, геометрия. Наряду с этим в него включены два дополнительных раздела: логика и множества, математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и обще­культурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания ма­тематического образования на данной ступени обучения.

Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесено к ступени общего среднего (полного) образования.

Содержание раздела «Алгебра» направлено на формирова­ние у учащихся ма­тематиче­ского аппарата для решения задач из разных разделов матема­тики, смежных предметов, окружа­ющей реальности. Язык алгебры подчерки­вает значение мате­матики как языка для построения математических моделей процессов и явлений реального мира. В задачи изуче­ния алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики, овладения навыками дедуктивных рассужде­ний. Преобразова­ние символьных форм вносит специфический вклад в разви­тие воображе­ния учащихся, их способностей к математическо­му творче­ству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с ир­рациональными выражениями, с тригоно­метрическими функ­циями и преобразова­ниями, входят в содержание курса мате­матики на старшей ступени обучения в школе.

Содержание раздела «Функции» нацелено на получение школьниками кон­кретных зна­ний о функции как важнейшей математической модели для описания и исследования разно­образных процессов. Изучение этого мате­риала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графиче­ский), вно­сит вклад в формирование представлений о роли математики в развитии цивилиза­ции и культуры.

Раздел «Вероятность и статистика» — обязательный ком­понент школь­ного образова­ния, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функцио­нальной грамот­ности - умений восприни­мать и критически анализиро­вать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, про­водить простей­шие вероятностные расчеты. Изучение основ комбинаторики позволит уча­щимся рассматривать случаи, осуществлять перебор и подсчет числа вариан­тов, в том чис­ле в про­стейших прикладных задачах.

При изучении статистики и вероятности расширяются представления о совре­менной кар­тине мира и методах его ис­следования, формируется понима­ние роли статистики как ис­точника социально значимой информации, и закладываются основы вероятностного мышле­ния.

Цель содержания раздела «Геометрия» — развить у учащих­ся пространствен­ное воображе­ние и логическое мышление пу­тем систематиче­ского изучения свойств геометриче­ских фигур на плоскости и в пространстве и применения этих свойств при реше­нии задач вычислительного и конструктив­ного характера. Существенная роль при этом отводится разви­тию геометри­ческой интуиции. Сочетание наглядности со строго­стью явля­ется неотъемлемой частью геометрических знаний. Материал, относящийся к блокам «Координаты» и «Векторы», в значи­тельной степени несет в себе меж­предметные знания, кото­рые находят применение, как в различных математи­ческих дисципли­нах, так и в смежных предметах.

Особенностью раздела «Логика и множества» является то, что представлен­ный в нем мате­риал преимущественно изуча­ется и используется в ходе рассмотре­ния различных вопросов курса. Соответствую­щий материал наце­лен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в уст­ной и письменной речи.

Раздел «Математика в историческом развитии» предназна­чен для формирова­ния представле­ний о математике как части человеческой куль­туры, для общего развития школьни­ков, для создания культурно-историче­ской среды обучения. На него не выделя­ется специальных уроков, усвоение его не контролиру­ется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рас­смотрении проблематики основного содержания математичес­кого образования.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: