 |
Рисунок 9.5 – Структурная схема электронного счетчика энергии переменного тока
|
|
|
|
Рисунок 9. 5 – Структурная схема электронного счетчика энергии переменного тока
Выходные импульсы ПНЧ подсчитываются счетчиком импульсов СИ, т. е. тем самым производится их интегрирование. Следовательно, показания СИ пропорциональны активной энергии.
Серийно выпускаемые в настоящее время электронные счетчики активной энергии переменного тока имеют класс точности 0, 5.
9. 2 Измерение активной мощности и энергии в трехфазных цепях
Как известно, независимо от характера нагрузки и схемы соединений трехфазной системы активная мощность и энергия за время определяются выражениями:
(9. 9а)
(9. 9б)
где индекс «ф» обозначает фазные напряжения и токи.
В симметричной трехфазной системе, в которой все фазные и линейные напряжения, токи и углы сдвига между фазными напряжениями и токами равны между собой, эти уравнения примут вид:
(9. 10а)
(9. 11б)
где - угол между фазными напряжениями и токами; индекс «л» обозначает линейные напряжения и токи.
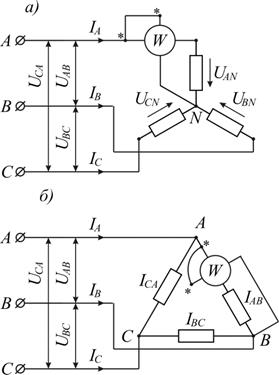
Рисунок 9. 6 – Схема измерения активной мощности в трехфазной цепи одним ваттметром при включении нагрузки звездой (а) и треугольником (б)
В трехфазной системе независимо от схемы соединения нагрузки - треугольником или звездой - мгновенное значение мощности системы равняется сумме мгновенных значений мощности отдельных фаз.
На этом основании для схемы соединения нагрузки звездой (рис. 9. 6, а) можно написать
где - мгновенные значения фазных напряжений; - мгновенные значения фазных токов.
На основании первого закона Кирхгофа можно в этом выражении исключить один из токов. Учитывая также, что, а уравнения для мгновенных значений мощности можно представить в трех формах:
|
|
|
К таким же выводам можно прийти и при включении нагрузки треугольником (рис. 9. 6, б).
Переходя от мгновенных значений активной мощности к средним, получим:
(9. 12а)
или
(9. 12б)
или
(9. 12в)
где и т. д., а также, и - действующие значения линейных напряжений и токов; и т. д. - углы сдвига фаз между соответствующими токами и напряжениями.
Из уравнений (9. 9) - (9. 12) видно, что для измерений мощности и энергии трехфазной системы могут быть применены один прибор (ваттметр или счетчик) два или три прибора.
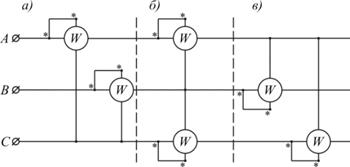
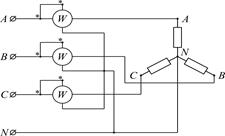
Метод одного прибора основывается на использовании выражений (9. 10) и применяется в симметричных трехфазных системах. При асимметричной системе, в которой значения токов и напряжений отдельных фаз не одинаковы, а также различаются углы сдвига фаз между векторами токов и напряжений, используется метод двух приборов. Наконец, в общем случае, в том числе и в четырехпроводной асимметричной системе на основании выражений (9. 9), применяется метод трех приборов.
В дальнейшем ограничимся рассмотрением только, методов измерения мощности, что дает также представление и о методах измерения энергии.
Метод одного прибора. Если трехфазная система симметрична, а фазы нагрузки соединены звездой с доступной нулевой точкой, то однофазный ваттметр включают по схеме рис. 9. 6, а и измеряют им мощность одной фазы. Для получения мощности всей системы показания ваттметра нужно утроить. Можно также измерить мощность при соединений фаз нагрузки треугольником, но при условии включения последовательной обмотки ваттметра в одну из фаз (рис. 9. 6, б).
Если нагрузка включена треугольником или звездой с недоступной нулевой точкой, то применяется включение ваттметра 1 с искусственной нулевой точкой (рис. 9. 7, а), которая создается с помощью двух дополнительных резисторов с активным сопротивлением
|
|
|
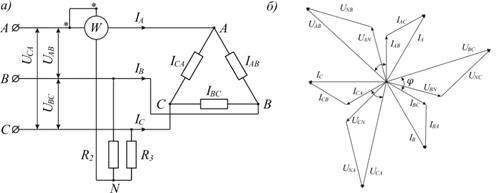
Рисунок 9. 7 – Схема измерения активной мощности в трехфазной цепи с искусственной нулевой точкой (а) и векторная диаграмма (б)
и. При этом необходимо выполнить условие ( - сопротивление параллельной цепи ваттметра).
На рис. 9. 7, б показана векторная диаграмма, соответствующая схеме рис. 9. 7, а. Напряжения, и на резисторах, образующих искусственную нулевую точку, можно рассматривать
|
|
|


