 |
Теоремы для двух и трех переменных
|
|
|
|
7. Коммутативные (переместительные) законы:
а Ù b = b Ù а
а Ú b = b Ú а
От перемены мест слагаемых сумма не меняется.
8. Ассоциативные (сочетательные) законы:
а Ù (b Ù c) = (a Ù b) Ù c ассоциативность конъюнкции.
а Ú (b Ú c) = (а Ú b) Ú c ассоциативность дизъюнкции.
Для записи умножения или сложения скобки можно опустить.
9. Дистрибутивные (распределительные) законы:
а) умножение относительно сложения
а Ù (b Ú c) = а Ù b Ú а Ú c
а (b + с) = аb + ас (в обычной алгебре)
б) сложение относительно умножения
a Ú b Ù c = (a Ú b) Ù (a Ú c)
a+bc ¹ (a+b) (a+c) (в обычной алгебре)
10. Законы инверсии (правило де Моргана)

11. Обобщение законов де Моргана, предложенное Шенноном:

т.е. инверсия дизъюнкции и конъюнкции получается заменой каждой переменной ее инверсией и одновременно взаимной заменой символов суммы и произведения.
12. Законы поглощения
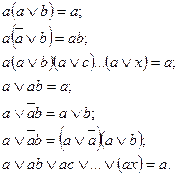
13. Закон контрапозиции  . Согласно закону контрапозиции два высказывания вида
. Согласно закону контрапозиции два высказывания вида 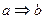 и
и  одновременно истинны или одновременно ложны. Вместо заданной теоремы можно доказать обратно противоположную теорему. Например. "Если m2 нечетно, то m - нечетно". Докажем что если m четно, то m2 четно. Действительно, если m = 2n, то m2 = 4n2.
одновременно истинны или одновременно ложны. Вместо заданной теоремы можно доказать обратно противоположную теорему. Например. "Если m2 нечетно, то m - нечетно". Докажем что если m четно, то m2 четно. Действительно, если m = 2n, то m2 = 4n2.
14. Закон транзитивности импликации (закон силлогизма).
(а Þ b) Ù (b Þ с) Þ(а Þ с)
15. Закон транзитивности эквиваленции.
(а Û b) Ù (b Û с) Þ(а Û с)
16. Закон противоположности.
(а Û b)Û (Øа ÛØb)
17. Законы склеивания (распространения).

Тавтологии. Равносильные формулы
ПФ, значения которых для любого набора переменных есть 1 (соответственно 0) будем называть тождественно истинными формулами, или тавтологиями (тождественно-ложными ПФ или противоречием).
|
|
|
Тавтологии играют в логике особо важную роль как формулы, отражающие логическую структуру предложений, истинных в силу одной только этой структуры. Для доказательства того, что ПФ является тавтологией достаточно построить таблицу истинности для этой ПФ. Перечислим некоторые основные тавтологии или законы логики. Обозначим | = А, что А тавтология. Справедливость | = и º вытекает из определений:
1. | = х º х - закон тождества
2. | =  º 0 - закон противоречия
º 0 - закон противоречия
3. | =  º1 - закон исключенного третьего
º1 - закон исключенного третьего
4. | =  º х - закон двойного отрицания
º х - закон двойного отрицания
5. | =  =
=  - закон идемпотентности
- закон идемпотентности
6.  -законы де Моргана
-законы де Моргана
7. | =  - закон контрапозиции
- закон контрапозиции
8. | =  - закон транзитивности импликации (закон силлогизма)
- закон транзитивности импликации (закон силлогизма)
9. | =  - закон противоположности
- закон противоположности
10.| =  - закон транзитивности эквиваленции
- закон транзитивности эквиваленции
Законы 1-3 выражают законы формальной логики, выведенные Аристотелем. Закон тождества требует, чтобы мысль, заключенная в высказывании не изменялась в течении всего рассуждения. Закон противоречия говорит, что одна и та же мысль не может быть одновременно и истинной и ложной.
В силу законов идемпотентности в алгебре логики нет показателей степени и коэффициентов (idem - "то же", potentia - сила).
Смысл законов де Моргана можно выразить так: отрицание дизъюнкции равно конъюнкции отрицаний и vice versa. Согласно закону контрапозиции два предложения вида  и
и  одновременно истинны или одновременно ложны.
одновременно истинны или одновременно ложны.
Две ПФ  и
и 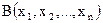 назовем равносильными, если для любых наборов
назовем равносильными, если для любых наборов  они принимают одинаковые значения.
они принимают одинаковые значения.
Это обозначается АºВ и читается "А равносильно В" (равносильность рефлексивна, симметрична и транзитивна).
Теорема 1. А º В тогда и только тогда, когда | = А Û В. Убедимся, что теорема верна, если докажем необходимость: если АºВ, то | = А Û В; достаточность: если | = А Û В, то А º В. Справедливость этих утверждений вытекает непосредственно из определений.
|
|
|
Принцип двойственности: Если две формулы, (не содержащие знаков Þ, и Û) равносильны, то двойственные ил формулы равносильны.
Две формулы называются двойственными, если каждую из них можно получить из другой заменой Ù, Ú, 1, 0 соответственно на Ú, Ù, 0 и 1 (X Ú 0 = Х Ù 1).
Обратные и противоположные теоремы. Для каждого предложения, формализованного импликацией А Þ В, можно составить три таких предложения В Þ А,  и
и  . Предложение В Þ А называется обратным данному, предложения
. Предложение В Þ А называется обратным данному, предложения  противоположным данному и
противоположным данному и  обратно противоположным. Для всякой теоремы вида "если А, то В" можно сформулировать обратное ей предложение "если В, то А". Однако не для всякой теоремы предложение ей обратное является истинным. Например: "если два прямоугольника конгруэнтны, то их площади равны", обратное: "Если площади двух прямоугольников равны, то они конгруэнтны" - неверно. Если А Þ В теорема, то А есть достаточное условие В, а В необходимое условие А. Если оба взаимообратных предложения А Þ В и В Þ А теоремы, т.е. предложение АÛ В теорема, то В является необходимым и достаточным условием А, а А достаточным и необходимым условием В (если два квадрата конгруэнтны...). Если А Þ В теорема, а В Þ А нет, то А - достаточное, но не необходимое условие В, а В - необходимое, но не достаточное условие А.
обратно противоположным. Для всякой теоремы вида "если А, то В" можно сформулировать обратное ей предложение "если В, то А". Однако не для всякой теоремы предложение ей обратное является истинным. Например: "если два прямоугольника конгруэнтны, то их площади равны", обратное: "Если площади двух прямоугольников равны, то они конгруэнтны" - неверно. Если А Þ В теорема, то А есть достаточное условие В, а В необходимое условие А. Если оба взаимообратных предложения А Þ В и В Þ А теоремы, т.е. предложение АÛ В теорема, то В является необходимым и достаточным условием А, а А достаточным и необходимым условием В (если два квадрата конгруэнтны...). Если А Þ В теорема, а В Þ А нет, то А - достаточное, но не необходимое условие В, а В - необходимое, но не достаточное условие А.
Для всякой теоремы А Þ В, можно составить противоположное предложение  , которое может быть истинным, но может и не быть истинным. Чтобы убедиться в этом, надо составить таблицу истинности.
, которое может быть истинным, но может и не быть истинным. Чтобы убедиться в этом, надо составить таблицу истинности.
Согласно закону контрапозиции два предложения вида  одновременно истинны или ложны. Вместо данной теоремы можно доказать обратно противоположную.
одновременно истинны или ложны. Вместо данной теоремы можно доказать обратно противоположную.
|
|
|


