 |
Критерии полноты Поста-Яблонского
|
|
|
|
Теорема о функциональной полноте была сформулирована в 1921 г. американским ученым Эмилем Постом и доказана советским ученым Яблонским С.В.
Система S булевых функций fi является полной тогда и только тогда, когда выполняются 5 условий: существует функция fi Î S, не сохраняющая константу нуль: fi Ï K0; функция fi Î S, не сохраняющая константу 1: fi Ï K1; нелинейная функция, не самодвойственная и немонотонная функция в системе S. Построим все булевы функции от двух переменных (табл.).
| переменные | булевы функции | ||||||||||||||||
| X1 | X2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
Индекс i функциональной переменной 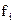
 равен десятичному эквиваленту этой функции, читаемому сверху вниз.
равен десятичному эквиваленту этой функции, читаемому сверху вниз.
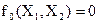 - константа 0
- константа 0
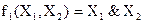 - конъюнкция
- конъюнкция

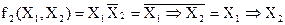 - левая коимпликация (читается “неправда, что если X1 то X2», префикс ко – от латинского conversus - обратный
- левая коимпликация (читается “неправда, что если X1 то X2», префикс ко – от латинского conversus - обратный
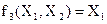

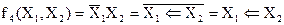 - правая коимпликация
- правая коимпликация
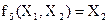
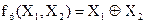 - сложение по модулю 2 (неравнозначность)
- сложение по модулю 2 (неравнозначность)
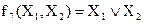 - дизъюнкция
- дизъюнкция
 - стрелка Пирса, функция Вебба
- стрелка Пирса, функция Вебба
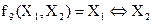 - эквивалентность
- эквивалентность
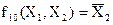 - отрицание X2
- отрицание X2
 - правая импликация («если X1 то X2»)
- правая импликация («если X1 то X2»)
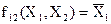 - отрицание X1 («если X1 то X2»)
- отрицание X1 («если X1 то X2»)
 - левая импликация
- левая импликация
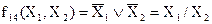 - штрих Шеффера
- штрих Шеффера
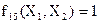
Для порождения всех базисов в P2 построим двумерную таблицу, каждой строке которой взаимно однозначно составим 11 функций, столбцу - класс, и в клетке (i, j) ставим 1, если 1 -функция не принадлежит j классу.
| идентификатор строки | номер функции fi | классы | ||||
| K0 | K1 | Kл | Kс | Kм | ||
| a | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e | ||||||
| g | ||||||
| k | ||||||
| m | ||||||
| n | ||||||
| p | ||||||
| r |
Из таблицы видно, что каждое, указанное ниже, покрытие порождает базис Bi.
|
|
|
П1 = {g} Û B1 – базис Вебба;
П2 = {p} Û B2 – базис Шеффера;
П3 = {a, n} Û B3 = {Þ, 0} – импликативный базис;
П4 = {b, m} Û B4 = {& Ø} – конъюнктивный базис Буля;
П5 = {m, e} Û B5 = {Ú Ø} – дизъюнктивный базис Буля;
П6 = {r, b, d} Û B6 = {Å, &, 1} – базис Жегалкина;
П7 = {m, n} Û B7 = {Þ, Ø} – базис Фреге.
Всего 17 базисов.
Наиболее часто приходится использовать базис Шеффера.
Вопросы для самопроверки
1. Составьте таблицы истинности для формул:
а) 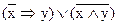 б)
б) 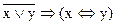
в) 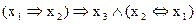 г)
г) 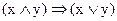
д) 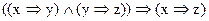
| x | y | 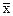
| 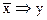
| 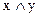
| 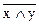
| 
|
3.2. Установите с помощью таблиц истинности какие из следующих формул - тавтологии:
а)  б)
б) 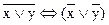
в) 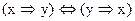 г)
г) 
д) 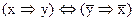 е)
е) 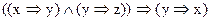
3. На основании каких законов логики получены следующие соотношения? Докажите их с помощью таблиц истинности:
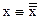 ;
; 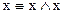 ;
; 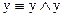 ;
;  ;
; 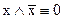 ;
; 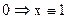 ;
;  ;
; 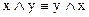 ;
; 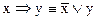 ;
; 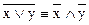 ;
; 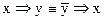 ;
; 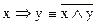 ;
; 
4. Какие из данных формул равносильны:
а) 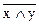 б)
б) 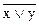 в)
в) 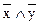 г)
г) 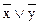
д) 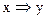 е)
е) 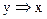 ж)
ж) 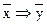 з)
з) 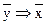
5. Полиция задержала 4 гангстеров, подозреваемых в краже автомобиля: Анри, Луи, Жоржа и Тома. При допросе они дали следующие показания: Анри: «Это был Луи», Луи: «Это сделал Том», Жорж: «Это не я», Том: «Луи лжет, говоря, что это я». Дополнительное расследование показало, что правду сказал только один из них. Кто украл машину?
| х | y | z | F1 | F2 |
Таблица к задаче 6
|
|
|
6. Составьте формулы, соответствующие данной таблице истинности (выберите рациональный способ). Упростите полученные формулы и изобразитеих в виде контактных схем.
7. Для каждой из данных формул найдите ее СДНФ и СКНФ:
а) 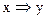 б)
б) 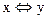 в)
в) 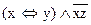
г) 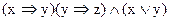
8. Напишите СДНФ представляющую: а) тавтологии с переменными х и у; б) тавтологии с переменными х, у и а; в) тождественно ложные формулы с переменными х, у и а.
Пример:  .
.
9. Составьте всевозможные таблицы истинности для формул с 2 переменными х и у. Выпишите СДНФ и СКНФ формул, соответствующих этим таблицам. Укажите 16 таких таблиц.
10. Один логик попал в плен дикарям в пещеру, имеющую 2 выхода. Вождь дикарей предложил логику следующий шанс на спасение: «Один выход ведет на свободу, другой на смерть. Сделать выбор тебе помогут два моих воина, одному из которых ты можешь задать единственный вопрос. Но предупреждаю тебя, что один из этих воинов всегда говорит правду, а другой всегда лжет». Что должен спросить логик?
11. Установите, какие из данных формул являются ДНФ, СДНФ, УНФ и СКНФ формул с переменными х, у и z:
а) 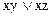 б)
б) 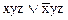 в)
в) 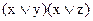
г) 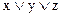 д)
д) 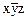 е)
е) 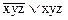
ж) 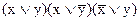
Примечание: Для приведения к СДНФ, если в какой-либо конъюнкции не содержится переменной я из числа переменных, входящих в исходную формулу, надо добавить к этой конъюнкции член (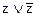 ) и применить закон распределительности конъюнкции относительно дизъюнкции (для приведения к СКНФ член
) и применить закон распределительности конъюнкции относительно дизъюнкции (для приведения к СКНФ член 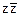 соответственно)
соответственно)
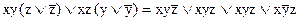 .
.
12. Приведите следующие формулы к СДНФ с помощью равносильных преобразований:
а) 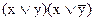 б)
б) 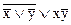 в)
в) 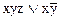
г) 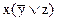 д)
д)  е)
е) 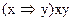
13. Приведите следующие формулы к СКНФ с помощью равносильных преобразований и проверьте их с помощью таблиц истинности:
а) 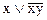 б)
б) 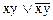 в)
в) 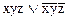
г) 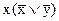 д)
д) 
Примечание: 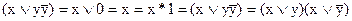 .
.
14. Найти все булевы функции от 2х переменных являющиеся:
а) линейными; б) монотонными; в) самодвойственными.
15. Установить является ли самодвойственной функция эквивалентности.
16. Привести пример монотонной функции, которая одновременно была бы линейной.
17. Убедиться, что функции Шеффера и Вебба не являются ни линейными, ни монотонными.
|
|
|


