 |
Производные и дифференциалы высших порядков
|
|
|
|
Пусть функция y = f (x) определена на множестве D и существует  . Тогда на D определена функция
. Тогда на D определена функция  . Если эта функция имеет производную в точке x Î D, то её называют производной второго порядка (или второй производной) функции f (x) в точке x.
. Если эта функция имеет производную в точке x Î D, то её называют производной второго порядка (или второй производной) функции f (x) в точке x.
Обозначается  ,
,  ,
, 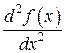 ,
,  .
.
Таким образом  .
.
Производные высших порядков определяются индуктивно. Если для любого  существует
существует  , то на D определена функция
, то на D определена функция  . Производная от этой функции (если она существует) в точке x Î D называется производной n–го порядка функции f (x) в точке x.
. Производная от этой функции (если она существует) в точке x Î D называется производной n–го порядка функции f (x) в точке x.
 .
.
Обозначается: 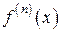 ,
,  ,
,  ,
,  .
.
Cчитают, что  .
.
Заметим, что если существует 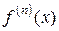 в точке х, то в некоторой окрестности точки
в точке х, то в некоторой окрестности точки  существует
существует  и все производные более низкого порядка k, k < n.
и все производные более низкого порядка k, k < n.
Если для функции y = f (x) в точке х существует 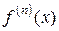 , то говорят, что функция n раз дифференцируема в этой точке.
, то говорят, что функция n раз дифференцируема в этой точке.
Пусть y = f (x) дважды дифференцируема на множестве D. Дифференциалом второго порядка функции f называется дифференциал от её дифференциала первого порядка и обозначается  . Таким образом
. Таким образом  .
.
Если х – независимая переменная, то
 .
.
Итак, 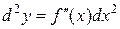 .
.
Дифференциал любого порядка определяется индуктивно. Предположим, что уже введён дифференциал (n -1)–го порядка  , и что y = f (x) дифференцируема n раз.
, и что y = f (x) дифференцируема n раз.
Дифференциалом n-го порядка функции f называется дифференциал от её дифференциала (n -1)-го порядка.
Обозначается  . Т. о.,
. Т. о.,  .
.
Аналогично, как для дифференциала второго порядка, получим
 .
.
Правило Лопиталя
При раскрытии неопределенностей  ,
,  кроме классических методов вычисления пределов, во многих случаях можно пользоваться правилом Лопиталя:
кроме классических методов вычисления пределов, во многих случаях можно пользоваться правилом Лопиталя:
Eсли  или
или  и существует предел отношения их производных
и существует предел отношения их производных  , то
, то  .
.
Это правило справедливо и в случае 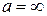 .
.
Пример 6.1. Применяя правило Лопиталя, найти пределы:
|
|
|
а)  ; б)
; б)  ; в)
; в)  .
.
Решение. Убедившись, что имеет место случай  или
или  , применяем правило Лопиталя.
, применяем правило Лопиталя.
а) 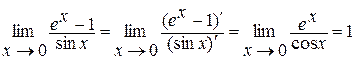 ,
,
б) 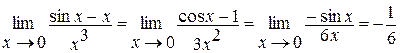 .
.
Здесь мы дважды применили правило Лопиталя и воспользовались первым замечательным пределом.
в)  .
.
При раскрытии неопределенностей  для применения правила Лопиталя, данное выражение надо преобразовать к неопределенностям
для применения правила Лопиталя, данное выражение надо преобразовать к неопределенностям  или
или  путем алгебраических преобразований.
путем алгебраических преобразований.
Пример 6.2. Найти пределы:
а) 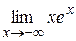 ; б)
; б)  .
.
Решение: а) Имеем неопределенность  . Приведем эту неопределенность к неопределенности
. Приведем эту неопределенность к неопределенности  , а затем применим правило Лопиталя:
, а затем применим правило Лопиталя:
 .
.
б) Имеем неопределенность  . Преобразуем к неопределенности
. Преобразуем к неопределенности  , после чего применим правило Лопиталя:
, после чего применим правило Лопиталя:


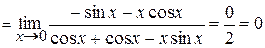 .
.
При раскрытии неопределенностей  ,
,  ,
,  рекомендуется найти предварительно предел логарифма искомой функции.
рекомендуется найти предварительно предел логарифма искомой функции.
Пример 6.3. Вычислить 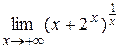 .
.
Решение. Имеем неопределенность  . Введем обозначение
. Введем обозначение
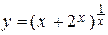 , тогда
, тогда  .
.  .
.
Получили неопределенность  , применяем правило Лопиталя:
, применяем правило Лопиталя:

 .
.
Так как  . Следовательно
. Следовательно  .
.
Пример 6.4. Пользуясь правилом Лопиталя, вычислить предел  .
.
Решение. В данном случае имеется неопределенность  , но от нее не удается избавится после однократного применения правила Лопиталя. В данном примере это правило приходится использовать три раза.
, но от нее не удается избавится после однократного применения правила Лопиталя. В данном примере это правило приходится использовать три раза.


 .
.
7. Применение производной к исследованию функций
и построению графиков
Исследование функций и построение их графиков следует проводить по следующей схеме.
1. Найти область определения функции.
Переменная величина  называется функцией переменной величины
называется функцией переменной величины  , если каждому допустимому значению
, если каждому допустимому значению  соответствует единственное значение
соответствует единственное значение  . Переменная величина
. Переменная величина  при этом называется независимой переменной или аргументом функции.
при этом называется независимой переменной или аргументом функции.
Множество всех значений аргумента, при которых функция принимает определенные действительные значения, называется областью определения этой функции. Множество всех значений функции называется областью ее значений.
|
|
|
Область определения и область значений функции f обозначают символами  и
и  соответственно. Область определения
соответственно. Область определения  называется симметричным множеством, если вместе с каждым элементом
называется симметричным множеством, если вместе с каждым элементом  оно содержит и противоположный элемент (
оно содержит и противоположный элемент ( ).
).
2. Исследовать, является ли функция четной или нечетной.
Функция  называется четной, если ее область определения
называется четной, если ее область определения  - симметричное множество и выполняется равенство
- симметричное множество и выполняется равенство  при всех
при всех  .
.
Функция f называется нечетной, если ее область определения  - симметричное множество и выполняется равенство
- симметричное множество и выполняется равенство  при всех
при всех  .
.
График четной функции симметричен относительно оси ординат ОY, а график нечетной функции – относительно начала координат. Поэтому, если исследуемая функция четная или нечетная, то ее достаточно исследовать при положительных значениях аргумента из области ее определения.
3. Исследовать, является ли функция периодической.
Множество  называется периодическим с периодом Т (
называется периодическим с периодом Т ( ), если для любого
), если для любого  выполняется
выполняется  и
и  .
.
Функция f называется периодической с периодом Т, если  - периодическое множество с периодом Т и для любого
- периодическое множество с периодом Т и для любого  выполняется равенство
выполняется равенство  .
.
График периодической с периодом Т функции переходит в себя при сдвиге на Т вдоль оси абсцисс.
4. Найти точки пересечения графика с осями координат и интервалы знакопостоянства, то есть промежутки на которых  или
или  .
.
5. Найти вертикальные асимптоты графика функции.
Прямая  на плоскости
на плоскости  называется вертикальной асимптотой функции
называется вертикальной асимптотой функции  , если один из односторонних пределов
, если один из односторонних пределов  или
или 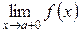 равен
равен  .
.
Таким образом, прямая  является вертикальной асимптотой функции
является вертикальной асимптотой функции  , если точка
, если точка  - точка разрыва второго рода для функции
- точка разрыва второго рода для функции  .
.
6. Исследовать поведение функции на бесконечности и найти ее горизонтальные и наклонные асимптоты.
Прямая  называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции  при
при  (
( ), если
), если  при
при  (
( ).
).
Теорема 1. Для существования наклонной асимптоты  при
при  функции
функции  необходимо и достаточно, чтобы при
необходимо и достаточно, чтобы при  выполнялись условия:
выполнялись условия:
1.  ,
,  ,
,
2.  ,
,  .
.
7. Найти точки экстремума и промежутки возрастания и убывания функции.
Функция  называется возрастающей (убывающей) на
называется возрастающей (убывающей) на  , если для любых
, если для любых  из неравенства
из неравенства 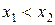 следует неравенство
следует неравенство 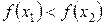 (
( ).
).
Возрастающие и убывающие функции называются монотонными.
Теорема 2 (достаточное условие монотонности). Пусть функция  определена и непрерывна на
определена и непрерывна на  и дифференцируема на
и дифференцируема на  . Если
. Если 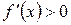 (
(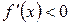 ), то
), то  возрастает (убывает) на
возрастает (убывает) на  .
.
|
|
|
Точка  называется точкой максимума (точкой минимума) функции
называется точкой максимума (точкой минимума) функции  , если во всех точках
, если во всех точках  , достаточно близких к точке
, достаточно близких к точке  и отличных от нее, выполнено неравенство
и отличных от нее, выполнено неравенство  (
( ).
).
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции.
Точка  называется точкой строгого максимума (строгого минимума) функции
называется точкой строгого максимума (строгого минимума) функции  , если во всех точках
, если во всех точках  , достаточно близких к точке
, достаточно близких к точке  и отличных от нее, выполнено неравенство
и отличных от нее, выполнено неравенство  (
(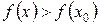 ).
).
Значение функции в точке  называется строгим максимумом (строгим минимумом) функции.
называется строгим максимумом (строгим минимумом) функции.
Точки максимума и минимума называются точками экстремума, а значения функции в них – экстремумами функции.
Теорема 3 (необходимое условие экстремума). Если функция  имеет в точке
имеет в точке  экстремум, то производная функции в этой точке равна нулю или не существует.
экстремум, то производная функции в этой точке равна нулю или не существует.
Точка  называется стационарной точкой функции
называется стационарной точкой функции  , если
, если  . Точка
. Точка  называется критической точкой функции
называется критической точкой функции  , если
, если  или не существует.
или не существует.
Из теоремы 3 следует, что точками экстремума могут быть только критические точки. Обратное не всегда верно.
Теорема 4 (Достаточное условие экстремума. Первое правило). Пусть в точке  производная функции
производная функции  обращается в нуль и при переходе через эту точку меняет знак, тогда точка
обращается в нуль и при переходе через эту точку меняет знак, тогда точка  - точка экстремума функции, причем если:
- точка экстремума функции, причем если:
1) 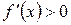 при
при  и
и 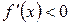 при
при  , то
, то  - точка строгого максимума;
- точка строгого максимума;
2) 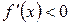 при
при  и
и 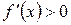 при
при  , то
, то  - точка строгого минимума.
- точка строгого минимума.
Теорема 5 (Достаточное условие экстремума. Второе правило). Если в точке  первая производная функции
первая производная функции  равна нулю, а вторая производная отлична от нуля, то
равна нулю, а вторая производная отлична от нуля, то  - точка экстремума, причем:
- точка экстремума, причем:
1)  - точка максимума, если
- точка максимума, если  ;
;
2)  - точка минимума, если
- точка минимума, если  .
.
Алгоритм нахождения точек экстремума для функции, непрерывной на  :
:
Найдем критические точки  функции
функции  на
на  . Расположим их в порядке возрастания:
. Расположим их в порядке возрастания:  . Они делят
. Они делят  на интервалы
на интервалы  ,
,  ,…,
,…,  . В каждом из них
. В каждом из них  , она знакопостоянна (положительна, или отрицательна). Для определения знака производной в интервале надо определить ее знак в любой точке интервала. Затем по изменению знака производной при переходе от одного интервала к другому определим точки экстремума по теореме 4.
, она знакопостоянна (положительна, или отрицательна). Для определения знака производной в интервале надо определить ее знак в любой точке интервала. Затем по изменению знака производной при переходе от одного интервала к другому определим точки экстремума по теореме 4.
|
|
|
8. Определение направлений выпуклости графика функции и точек перегиба.
Пусть функция  дифференцируема на
дифференцируема на  . Тогда существует касательная к графику функции
. Тогда существует касательная к графику функции  в любой точке
в любой точке  ,
,  , причем эти касательные не параллельны оси
, причем эти касательные не параллельны оси  .
.
Функция  называется выпуклой вверх (вниз) на
называется выпуклой вверх (вниз) на  , если график функции в пределах
, если график функции в пределах  лежит не выше (не ниже) любой из своих касательных.
лежит не выше (не ниже) любой из своих касательных.
Теорема 6 (достаточное условие выпуклости). Пусть функция  дважды дифференцируема на
дважды дифференцируема на  . Тогда если
. Тогда если  (
( ) на
) на  , то функция выпукла вниз (вверх) на
, то функция выпукла вниз (вверх) на  .
.
Точка  называется точкой перегиба функции
называется точкой перегиба функции  , если при переходе через эту точку меняется направление выпуклости функции
, если при переходе через эту точку меняется направление выпуклости функции  .
.
Теорема 7 (необходимое условие перегиба). Если в точке перегиба  функции
функции  вторая производная существует и непрерывна, то она в этой точке равна нулю.
вторая производная существует и непрерывна, то она в этой точке равна нулю.
Теорема 8 (достаточное условие перегиба). Если 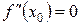 и
и
1)  меняет знак при переходе через
меняет знак при переходе через  , то
, то  - точка перегиба функции
- точка перегиба функции  ;
;
2)  не меняет знака при переходе через
не меняет знака при переходе через  , то
, то  не является точкой перегиба функции
не является точкой перегиба функции  .
.
9. Построение графика функции.
Графиком функции  называется множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости.
называется множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости.
Пример 7.1. Исследовать функцию  на монотонность и направление выпуклости, найти экстремумы и точки перегиба.
на монотонность и направление выпуклости, найти экстремумы и точки перегиба.
Решение.
1. Найдем область определения функции.
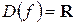 , так как данная функция – многочлен.
, так как данная функция – многочлен.
2. Исследуем функцию на монотонность, найдем точки экстремума.
Найдем вначале критические точки функции.
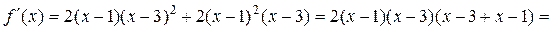
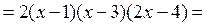
 .
.
 , так как производная тоже является многочленом.
, так как производная тоже является многочленом.
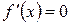 Û
Û  или
или  , или
, или  . Следовательно,
. Следовательно,  ,
,  ,
,  – критические точки функции.
– критические точки функции.
 Нанесем критические точки функции на числовую прямую и определим знаки производной в каждом из получившихся промежутков.
Нанесем критические точки функции на числовую прямую и определим знаки производной в каждом из получившихся промежутков.
На промежутках  ,
,  функция убывает, на промежутках
функция убывает, на промежутках  ,
,  функция возрастает.
функция возрастает.
Точки  и
и  – точки минимума функции,
– точки минимума функции,  .
.
Точка  – точка максимума функции,
– точка максимума функции, 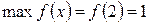 .
.
3. Исследуем функцию на направление выпуклости, найдем точки перегиба.

 .
.
 Û
Û  Û
Û 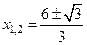 .
.
Нанесем точки х 1 и х 2 на числовую прямую и определим знаки второй производной в каждом из получившихся промежутков.
 На промежутках
На промежутках  и
и  функция выпукла вниз, на промежутке
функция выпукла вниз, на промежутке  функция выпукла вверх. Точки
функция выпукла вверх. Точки  и
и  являются точками перегиба.
являются точками перегиба.
Пример 7.2. Исследовать функцию  на монотонность и направление выпуклости, найти экстремумы и точки перегиба.
на монотонность и направление выпуклости, найти экстремумы и точки перегиба.
Решение.
1. Найдем область определения функции.
 :
: 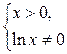 Û
Û  Þ
Þ  .
.
2. Исследуем функцию на монотонность, найдем точки экстремума.
 ,
,  .
.
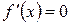 Û
Û  Û
Û  . Следовательно,
. Следовательно,  – критическая точка функции.
– критическая точка функции.
Нанесем область определения функции и критическую точку на числовую прямую. Определим знаки производной на каждом из получившихся промежутков.
|
|
|
 На промежутках
На промежутках 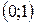 ,
,  функция убывает, на промежутке
функция убывает, на промежутке  функция возрастает. Точка
функция возрастает. Точка  – точка максимума,
– точка максимума, 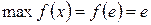 .
.
3. Определим направление выпуклости графика функции и найдем точки перегиба.
 .
.

 Û
Û  Û
Û 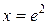 .
.
 Точка
Точка 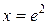 - точка возможного перегиба. Определим знаки второй производной в промежутках
- точка возможного перегиба. Определим знаки второй производной в промежутках 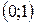 ,
,  ,
,  .
.
На промежутках 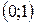 ,
,  функция выпукла вверх, на промежутке
функция выпукла вверх, на промежутке  функция выпукла вниз. Точка
функция выпукла вниз. Точка 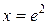 – точка перегиба.
– точка перегиба.
Пример 7.3. Провести полное исследование функции  и построить ее график.
и построить ее график.
Решение. 1.  .
.
2. Функция не является ни четной, ни нечетной.
3. Функция не является периодической.
4. Найдем точки пересечения графика с осями координат и промежутки знакопостоянства. Ось О х график не пересекает, так как  для всех
для всех  . Ось О у:
. Ось О у:  ,
,  .
.
 при
при  ,
,  при
при 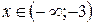 .
.
5. Функция непрерывна на области определения, так как является элементарной, 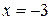 – точка разрыва. Исследуем характер разрыва:
– точка разрыва. Исследуем характер разрыва:
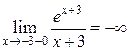 ,
,  .
.
Следовательно, 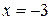 – точка разрыва второго рода, прямая
– точка разрыва второго рода, прямая 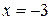 – вертикальная асимптота графика функции.
– вертикальная асимптота графика функции.
6. Исследуем поведение функции при  и при
и при  :
:
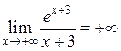 ,
,  . Следовательно, прямая
. Следовательно, прямая 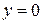 – горизонтальная асимптота графика функции при
– горизонтальная асимптота графика функции при  .
.
Так как  , то других наклонных асимптот при
, то других наклонных асимптот при  нет.
нет.
Выясним, есть ли наклонные асимптоты при  :
:
 . Следовательно, при
. Следовательно, при  наклонных асимптот нет.
наклонных асимптот нет.
7. Исследуем функцию на монотонность и экстремум.
 ,
, 

 – точка минимума,
– точка минимума,  – минимум.
– минимум.
8. Исследуем функцию на направление выпуклости и перегиб.

= 
 .
.


 на
на  ,
,  не существует в точке
не существует в точке 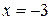 . Точек перегиба нет.
. Точек перегиба нет.
9. Построим график функции (рис. 4).
Рисунок 4 – Иллюстрация к примеру 7.3.
Пример 7.4. Исследовать функцию  и построить её график.
и построить её график.
Решение. Исследуем данную функцию.
1. Областью определения функции является множество  .
.
2. Функция не является ни четной, ни нечетной.
3. Функция не является периодической.
4. Точки пересечения графика данной функции с осями координат: 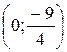 и
и  . Ордината точки графика
. Ордината точки графика  при
при  ,
,  при
при  .
.
5. Так как функция является элементарной, то она непрерывна на всей области определения. Легко находим, что 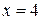 - вертикальная асимптота, причем:
- вертикальная асимптота, причем:
 ,
,  .
.
6. Исследуем поведение функции на бесконечности и найдем горизонтальные и наклонные асимптоты:
Так как  , то горизонтальных асимптот нет.
, то горизонтальных асимптот нет.
 ,
,

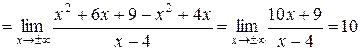 .
.
Таким образом, существует единственная наклонная асимптота 
7. Исследуем функцию на монотонность и найдем экстремумы:

 .
.
Из  следует
следует  , откуда
, откуда  ,
,  .
.
В интервале 
 , следовательно, функция возрастает в этом интервале; в
, следовательно, функция возрастает в этом интервале; в 
 , т. е. функция убывает. Поэтому точка
, т. е. функция убывает. Поэтому точка 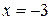 является точкой максимума:
является точкой максимума:  . В интервале
. В интервале 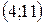
 , следовательно, функция убывает на этом интервале; в
, следовательно, функция убывает на этом интервале; в 
 , т. е. функции возрастает. В точке
, т. е. функции возрастает. В точке  имеем минимум:
имеем минимум:  .
.
8. Исследуем график функции на направление выпуклости и определим точки перегиба. Для этого найдем

 .
.
Очевидно, что в интервале 
 , следовательно, в этом интервале кривая выпукла вверх; в интервале
, следовательно, в этом интервале кривая выпукла вверх; в интервале 
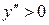 , т. е. в этом интервале кривая выпукла вниз. Так как при
, т. е. в этом интервале кривая выпукла вниз. Так как при 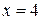 функция не определена, то точка перегиба отсутствует.
функция не определена, то точка перегиба отсутствует.
9. График функции изображен на рис. 5.

Рисунок 5 – Иллюстрация к примеру 7.3.
8. Нахождения наибольшего и наименьшего значений
непрерывной функции на отрезке
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на отрезке:
1) Найти все критические точки функции, принадлежащие отрезку  ;
;
2) Вычислить значения функции в этих точках и на концах отрезка;
3) Из полученных значений выбрать наибольшее и наименьшее.
Пример 8.1. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке  .
.
Решение. 1) Найдем критические точки функции.
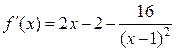 ,
, 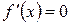 Û
Û  Û
Û
 Û
Û  .
.
На отрезке  знаменатель не обращается в нуль. Следовательно, дробь равна нулю тогда и только тогда, когда числитель равен нулю:
знаменатель не обращается в нуль. Следовательно, дробь равна нулю тогда и только тогда, когда числитель равен нулю:
 Û
Û  Û
Û 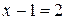 Û
Û  .
.
Значит,  – критическая точка функции. Она принадлежит данному отрезку.
– критическая точка функции. Она принадлежит данному отрезку.
Найдем значение функции в критической точке:
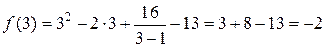 .
.
2) Найдем значения функции на концах отрезка:
 ,
,  .
.
3) Из полученных значений выбираем наибольшее и наименьшее:
 ,
,  .
.
9. Задачи на отыскание наибольших и наименьших
значений величин
При решении задач на вычисление наименьших и наибольших значений величин надо прежде всего определить, для какой величины в задаче требуется найти наименьшее или наибольшее значение. Эта величина и будет исследуемой функцией. Затем одну из величин, от изменения которых зависит применение функции, следует взять за независимую переменную и выразить через неё функцию. При этом нужно в качестве независимой переменной выбрать ту величину, через которую исследуемая функция выражается проще всего. После этого решается задача на нахождение наименьшего и наибольшего значения полученной функции в некотором промежутке изменения независимой переменной, которое обычно устанавливается из самого существа задачи.
Пример 9.1. Найти высоту конуса наибольшего объёма, который можно вписать в шар радиуса  .
.
 Решение. Обозначив радиус основания, высоту и объём конуса соответственно
Решение. Обозначив радиус основания, высоту и объём конуса соответственно  ,
,  и
и  , запишем
, запишем  . Это равенство выражает зависимость от двух переменных
. Это равенство выражает зависимость от двух переменных  и
и  ; исключим одну из этих величин, а именно
; исключим одну из этих величин, а именно  . Для этого из прямоугольного треугольника
. Для этого из прямоугольного треугольника  выводим (по теореме о квадрате перпендикуляра, опущенного из вершины прямого угла на гипотенузу):
выводим (по теореме о квадрате перпендикуляра, опущенного из вершины прямого угла на гипотенузу):
Рисунок 6 – Иллюстрация к примеру 9.1.


