Основные термины и понятия

ЛАБОРАТОРНАЯ РАБОТА №1

ПРЯМОЕ ИЗМЕРЕНИЕ С МНОГОКРАТНЫМ НАБЛЮДЕНИЕМ
ПРИ НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ ИЗМЕРЯЕМОЙ ВЕЛИЧИНЫ

 

Цели и задачи работы

Цель: познакомится с методом обработки прямых измерений с многократным наблюдением.

Задачи:

1. Познакомится с основными терминами и положениями процесса измерения

2. Провести прямое измерение с многократным наблюдением

3. Определить погрешность.

 

Теоретические положения

Основные термины и понятия

Физическая величина – это характеристика одного из свойств физиче­ского объекта (системы, явления или процесса) (вес, расстояние). Качественно одна и та же физическая величина может иметь различное количественное выражение характеризующееся её размером. Помимо физических величин существуют математические, социальные, экономические и пр. величины. Метрология занимается измерением только физических величин.

Измерение физической величины заключается в сравнении измеряе­мой величины с её условно принятой единицей, с целью получения значения этой величины. Измерение производится с по­мощью технических средств, хранящих единицу, или воспроизводящих шкалу физической величины.

В зависимости от принятой единицы один и тот же размер ФВ может иметь различные значения.

Значение физической величины выражает­ся произведением ее числового значения на выбранную для этой величины единицу. Числовое значение — это отвлеченное число.

Единица физической величины – физическая величина, которой условно присвоено числовое зна­чение, равное 1.

Пример: значение длины можно выразить как L = 0,202 м = 20,2 см = 202 мм. Сле­довательно, числовое значение физической величины с изменением размера единицы изменяется. Размер величины и ее значение при этом будут одними и теми же.

Основное уравнение метрологии:

 

Q = q ·[ Q ] + [ Q ₀],

 

где Q – размер физической величины, q – значение, [ Q ] – единица физической величины, [ Q ₀] начальное значение шкалы.

Различают истинное значение физической величины, идеально отражаю­щее свойства материального объекта, и действительное – значение, най­денное экспериментально как результат измерения.

Не следует отождествлять понятие измерение с понятием наблюдение при измерении – экспериментальной операцией, выполняемой в процессе измерения. Результат наблюдения – это одно значение (отсчет) измеряемой величины. Результат измерения получается после математической обработки всех отсчетов.

Измерением с однократными наблюдениями называется измерение, при котором каждый отсчет получен при различных значениях физических величин, связанных с измеряемой величиной.

Пример: измерение деформации конструкции в различных местах при различных нагрузках.

Измерением с многократными наблюдениями называется измере­ние, при котором все отсчеты получены при фиксированных значениях физи­ческих величин, связанных с измеряемой величиной.

Пример: измерение прочности бетона методом пластических деформаций – молотком Кашкарова.

Существует несколько основных видов измерений:

Прямым измерением называется измерение физической величины, при котором ее значение находят непосредственно из опытных данных.

Примеры: измерение длины с помощью линейки; измерение сопротивления ом­метром.

Косвенным измерением называется измерение физической величины, при котором ее значение находят на основании известной зависимости между этой величиной и величинами, значения которых получены прямыми измере­ниями.

Пример: определение площади прямоугольника по его длине и ширине.

Совокупные измерения, при которых одновременно проводятся измерения нескольких одноименных величин и искомое значение величины определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях. Например, значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений масс различных сочетаний гирь.

Совместные измерения, при которых одновременно проводится измерения двух или нескольких неодноименных величин для определения зависимости между ними, например, зависимость длины объекта от температуры.

Часто при измерении удобнее работать не с реальным объектом, а с моделью объекта измерения – это абстрактный, как правило, идеализированный образ реального объекта.

Примеры: материальная точка, абсолютно твердое тело, идеальный шарнир, жесткая заделка, конструкция моделируемая как стержень.

Также не следует путать понятия метод и методика измерения.

Метод измерений - это совокупность приемов сравнения измеряемой ве­личины с её единицей. Метод измерений осуществляется в соответствии с мо­делью объекта измерения и доступным набором технических средств.

Методика выполнения измерений -установленная совокупность операций и правил при измерении, выполнение которых обеспечивает получение необходимых результатов измерений в соответствии с тем или иным методом измерений.

Примеры: Базовый метод определения морозостойкости бетона реализуется методикой изложенной в ГОСТ 10060.1-95. Структурно-механический метод ускоренного определения морозостойкости реализуется методикой изложенной в ГОСТ 10060.4-95. Один и тот же метод в разных государствах и в разное время осуществлялся по различным стандартам, т.е. разными методиками.

Основной показатель качества измерения – то, на сколько близок полученный результат истинному значению измеряемой величины.

Истинной погрешностью измерения называется отклонение результата из­мерения физической величины (действительного значения) от ее истинного значения. Эта величина по определению неизвестна, поэтому принято погрешность характеризо­вать, так называемым, доверительным интервалом, в котором с опреде­ленной степенью достоверности содержится истинное значение. Середина это­го интервала совмещается с оценкой истинного значения – действительным значением измеряемой физической величины 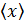(Рис. 1).

 

Рис. 1. Результат измерений

Доверительной вероятностью (надежностью) результата серии на­блюдений называется вероятность P, с которой доверительный интервал включает истинное значение измеряемой величины. Как правило, P принимается равным 95%, в особых случаях – 99% и более, но это значительно увеличивает доверительный интервал (рис. 2). И как следствие значение погрешности. Доверительный интервал не может быть равен 100%.

Границы доверительного интервала определяются на основании методов математической статистики и теории вероятностей. Для этого нужно знать форму распределения случайной величины – результатов измерения. Как правило, для большинства измерений характерно нормальное (Гаусово) распределение, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:

где параметр μ – математическое ожидание (среднее значение), а параметр σ – среднеквадратическое отклонение (σ ² – дисперсия) распределения:

Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии)

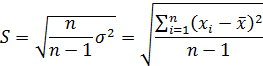
где σ ² – дисперсия; x_i – i -й элемент выборки; n – объём выборки; – среднее арифметическое выборки.

Один из классических методов определения погрешности – правило трёх сигм () – практически все значения нормально распределённой случайной величины лежат в интервале ) – приблизительно с 0,9973 вероятностью значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина 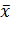истинная, а не полученная в результате обработки выборки). Если же истинная величина 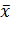неизвестна, то следует пользоваться не , а S. Таким образом, правило трёх сигм преобразуется в правило трёх S.

Часто требуется определить не погрешность, исходя из заданной надежности измерения, а одностороннее ограничение измеряемого параметра. Это подразумевает, что определенная контролируемая величина будет больше (или меньше) установленного придела с определенной вероятностью.

Обеспеченность значения величины – для случайных величин, для которых неблагоприятным является превышение какого-либо значения, - вероятность непревышения этого значения, а для которых неблагоприятным является занижение – вероятность незанижения.

Пример: Нормативное сопротивление стали . определяется с обеспеченностью 95%, это подразумевает, что 95% образцов материала имеют прочность большую, чем .

 

Рис. 2. Правило 3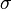

 

При увеличении надежности измерения погрешность растет.

Рис. 3. Связь доверительного интервала с
надежностью измерения.

 

Погрешность выражается в виде абсолютной и относительной по­грешности.

Абсолютная погрешность равна модулю разности между оценкой и границей интервала, т.е.полуширине доверительного интервала при симметричной форме распределения. Как правило обозначается D. Размерность абсолютной погрешности совпадает с размерностью измеряемой величины.

Относительная погрешность равна отношению абсолютной погреш­ности к оценке истинного значения. Как правило, эту погрешность выражают в процентах либо в долях единицы:

где 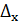– абсолютная погрешность, ­­– результат измерения.

Для оценки погрешности некоторых средств измерений используется приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности средства измерения к нормирующему значению (например, к диапазону шкалы).

Пример: Твердость металла 300 HB с абсолютной погрешностью Тогда абсолютная погрешность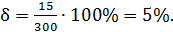

Величину, обратную относительной погрешности, называют точностью измерений.

Часто для оценки разброса случайных величин в технической литературе можно встретить термин «коэффициент вариации». Этот показатель определяется согласно формуле

При сравнении результатов измерения одной и той же физической величины поступают следующим образом. Если доверительные интервалы перекрываются, то говорят, что различия незначимые и результаты измерений согласуются. В противном случае различия считаются значимыми и результаты измерений не согласуются. Тут нужно заметить, что при разном значении надежности одни и те же результаты измерений могут оказаться как согласованными, так и не согласованными.

По влиянию на результат измерения можно выделить следующие классы погрешности:

Случайная погрешность – погрешность, изменяющаяся случайным образом при повторении измерений. Влияние можно снизить, увеличив количество отсчетов. Оптимальным количеством является 5-7 отсчетов.

Систематическая погрешность – погрешность, остающаяся посто­янной или закономерно изменяющаяся при повторении измерений. Исключается после обнаружения введением поправки в результат измерения или в каждый из отсчетов.

Пример: Спешащие часы вносят погрешность в измерение времени, в прямой зависимости от величины измеряемого диапазона.

Учет и исключение (или уменьшение) систематической погрешности представляют одну из самых сложных задач теории измерений. Способы решения этой задачи зависят от конкретных видов измерений, и не существует общей методики ее решения. Часто используется подход, основанный на всесторон­нем теоретическом анализе процедуры измерения и характеристик при­меняемой аппаратуры. Такой анализ может дать оценку границ систематиче­ской погрешности. При точных измерениях оценка систематической погреш­ности производится по результатам измерения искомой величины различными, принципиально независимыми методами с применением различной аппарату­ры. Многие современные способы анализа систематической погрешности ис­пользуют аппарат математической статистики (дисперсионный, регрессион­ный, корреляционный, спектральный анализ), теории принятия решений, тео­рии игр и др.

Наиболее распространенные экспериментальные методы определения систематической погрешности основаны на измерении заранее известной физической величины, или на измерении одной и той же величины при помощи более точного средства измерения или метода измерения. Так же применяется длительное наблюдение за измеряемой величиной, с целью выявить закономерность в изменениях показаний прибора – что будет являться подтверждением наличия систематической погрешности (при условии, что измеряемое значение остаётся неизменным).

Промах (грубая ошибка) – погрешность, существенно превосходящая ожидаемую при заданных условиях. Выявляется по статистическим критериям, например по критерию Шовене или методом 3 сигм. Выявленный отсчет с промахом исключается из обрабатываемых данных измерения. Промахи относятся к аномальным результатам измерений, которые могут быть следствием кратковременного воздействия на процесс измерения некото­рого мешающего фактора, преобладающего над остальными. Промах может быть вызван ошибкой оператора, проводящего измерение, или сбоем измери­тельной аппаратуры. В этих случаях аномальный результат должен быть от­брошен. Однако отбрасывание аномальных данных является спорным вопро­сом, по которому у специалистов нет единого мнения. Например, из истории физики известно, что именно аномальные результаты экспериментов привели к великим открытиям. Поэтому при научных исследованиях и в большинстве технических измерений необходимо тщательно проанализировать причину промаха, в частности, многократно повторив эксперимент. Тем не менее, в хорошо изученной ситуации, если не удается найти внешнюю причину прома­ха, вопрос об отбрасывании аномального отсчета должен быть решен на осно­ве обработки всех данных эксперимента.

По источникам погрешности различают следующие ее виды:

Методическая погрешность – погрешность, обусловленная несовер­шенством метода измерений. Характерна для непрямых методов измерения.

Пример – допущение о параллельности и прямолинейности стен при замере площади помещения; определение поверхностной твердости бетона полотком Кашкарова при определении прочности материала.

Инструментальная погрешность – погрешность средств измерений (приборов). Присутствует всегда, когда есть средство измерения. Может нормироваться в явном виде – в виде указания погрешности средства измерения, или функциональной зависимости погрешности от какой либо влияющей величины, может быть указана в виде класса точности средства измерения. Принимается не менее половины цены деления средства измерения и половины шага квантования для цифровых приборов (шаг квантования – шаг изменения показаний цифрового прибора).

Субъективная погрешность – погрешность, вносимая субъектом, проводящим эксперимент. Возникает в следствии неточности использования средства измерения, или неточности взятия отсчета с средства измерения. Величина может завесить как от условий и характера измерений, так и от личных качеств оператора.

Пример: погрешность от параллакса - т.е. от неправильного направления взгляда при отсчете показаний стрелочного прибора.

Погрешность из-за неоднородности измеряемой величины. Часто на практике нужно провести измерение величины с неоднородным проявлением по объекту измерения. В результате неизбежно возникает случайная погрешность.

Пример: измерение нагрузки на перекрытие при обследовании конструкций – величина нагрузки вследствие неровности перекрытия и толщин слоёв будет различной в разных местах вскрытия конструкции.

Дополнительная погрешность – погрешность, обусловленная влиянием факторов, которые не учтены в модели объекта измерения. Возникает, как правило, в следствии выхода в процессе измерения за границы интервалов условий измерений (диапазон температур, влажности, скачки напряжения и т.п.), для которых разработана методика измерений или средство измерений.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: