 |
Учет неисключаемой части систематической погрешности.
|
|
|
|
При наличии нескольких систематических погрешностей необходимо их объединить.
где Θни i - размер i -й неисключенной систематической погрешности; k - коэффициент, определяемый принятой доверительной вероятностью. Коэффициент k принимают равным 1,1 при доверительной вероятности P = 0,95. При доверительной вероятности P = 0,99 коэффициент k принимают 1,4, если число суммируемых неисключенных систематических погрешностей более четырех. Если же число суммируемых погрешностей равно четырем или менее четырех, то коэффициент k определяют по графику зависимости (см. рис. 3).
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.
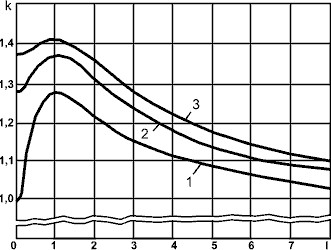
Рис. 4. График зависимости k = f (m, l), где m - число суммируемых погрешностей; 
; кривая 1 для m = 2; кривая 2 для m = 3; кривая 3 для m = 4. При трех или четырех слагаемых в качестве 
принимают составляющую, по числовому значению наиболее отличающуюся от других, в качестве 
следует принять ближайшую к составляющую.
При наличии 2-х составляющих погрешности: неисключаемой систематической и случайной необходимо их объединить.
В случае, если 
, неисключенными систематическими погрешностями пренебрегают, и принимают значение погрешности результата Δ= 
. Если 
случайной погрешностью пренебрегают и принимают значение погрешности результата Δ= 
.
В этих случаях погрешность, возникающая из-за пренебрежения одной из составляющих, не превышает 15%.
В случае, если вышеприведённые неравенства не выполняются, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключённых систематических погрешностей, рассматриваемых как случайные величины. Допускается значение погрешности результата измерения Δ вычислить по формуле
|
|
|
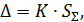
где K - коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;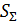 
- оценка суммарного среднего квадратического отклонения результата измерения.
Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле:
Коэффициент K вычисляют по эмпирической формуле
Форма записи результатов измерений
Запись результата измерения.
Оформление результатов измерений – по МИ 1317-86.
При симметричной доверительной погрешности результаты измерений представляют в форме:
P,
где 
– исправленный результат измерения, Δ – абсолютная погрешность, 
– относительная погешность, P – надежность измерения.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности Δ.
Значение погрешности округляется до двух значащих цифр, при этом отбрасываемый разряд округляется в большую сторону. Допускается округление до одной значащей цифры, в соответствием со стандартными математическими правилами (5-ка округляется в большую сторону).
Надежность измерения указывается в случае необходимости – когда методика измерения отсутствует, либо не оговаривает значение надежности.
Значение единиц измерения в результате указывается один раз, после величины абсолютной погрешности.
| Примеры записи и округления результатов измерения | |
| Результат до округления | Результат после округления |
| 32556±654 кг, P =95% | 32560±660 кг,  , P =95%
|
| 0,00600±0,00151 кг, P =99% | 0,0060±0,0016 кг,  P =99%
|
Вопросы для контроля
Часть 1. Теоретические понятия
1. Физическая величина
2. Размер физической величины
3. Измерение физической величины. Отсчеты при измерении
|
|
|
4. Значение физической величины. Истинное и действительное значение.
5. Единица физической величины
6. Измерения с однократными наблюдениями
7. Измерения с многократными наблюдениями
8. Прямые измерения
9. Косвенные измерения
10. Совокупные измерения
11. Совместные измерения
12. Модель объекта измерения
13. Метод и методика измерения
14. Истинная погрешность
15. Доверительный интервал
16. Доверительная вероятность (надежность) измерения. Зависимость погрешности от надежности измерения
17. Среднеквадратическое отклонение и стандартное отклонение
18. Правило трех сигм
19. Абсолютная погрешность.
20. Относительная погрешность
21. Приведённая погрешность
22. Обеспеченность значения величины.
23. Коэффициент вариации.
24. Согласованность различных измерений одной и той же физической величины.
25. Случайная погрешность.
26. Систематическая погрешность.
27. Промах (грубая ошибка).
28. Методическая погрешность.
29. Инструментальная погрешность.
30. Субъективная погрешность. Параллакс.
31. Погрешность из-за неоднородности измеряемой величины.
32. Дополнительная погрешность.
Часть 2. Практическое выполнение
1. Определение значения измеряемой величины. Исправленное значение измеряемой величины.
2. Проверка отсчетов на наличие грубой ошибки по критерию Шовене.
3. Расчет случайной погрешности.
4. Учёт нескольких систематических погрешностей одновременно.
5. Учет неисключенной части систематических погрешностей.
6. Учёт исключённых частей систематической погрешности.
7. Правила записи результата измерения.
Приложение 1
Отбор промахов по критерию Смирнова
| Z | М | Z | М | Z | М | Z | М | Z | М |
| 1.00 | 1.40 | 1.80 | 2.20 | 2.60 | |||||
| 1.02 | 1.42 | 1.82 | 2.22 | 2.62 | |||||
| 1.04 | 1.44 | 1.84 | 2.24 | 2.64 | |||||
| 1.06 | 1.46 | 1.86 | 2.26 | 2.66 | |||||
| 1.08 | 1.48 | 1.88 | 2.28 | 2.68 | |||||
| 1.10 | 1.50 | 1.90 | 2.30 | 2.70 | |||||
| 1.12 | 1.52 | 1.92 | 2.32 | 2.72 | |||||
| 1.14 | 1.54 | 1.94 | 2.34 | 2.74 | |||||
| 1.16 | 1.56 | 1.96 | 2.36 | 2.76 | |||||
| 1.18 | 1.58 | 1.98 | 2.38 | 2.78 | |||||
| 1.20 | 1.60 | 2.00 | 2.40 | 2.80 | |||||
| 1.22 | 1.62 | 2.02 | 2.42 | 2.82 | |||||
| 1.24 | 1.64 | 2.04 | 2.44 | 2.84 | |||||
| 1.26 | 1.66 | 2.06 | 2.46 | 2.86 | |||||
| 1.28 | 1.68 | 2.08 | 2.48 | 2.88 | |||||
| 1.30 | 1.70 | 2.10 | 2.50 | 2.90 | |||||
| 1.32 | 1.72 | 2.12 | 2.52 | 2.92 | |||||
| 1.34 | 1.74 | 2.14 | 2.54 | 2.94 | |||||
| 1.36 | 1.76 | 2.16 | 2.56 | 2.96 | |||||
| 1.38 | 1.78 | 2.18 | 2.58 | 2.98 |
Приложение 2
|
|
|
Коэффициент Стьюдента (t -критерий)
| P | ||||||
| f * | 0.5 | 0.9 | 0.95 | 0.98 | 0.99 | 0.999 |
| 6.3 | 12.7 | 31.8 | 63.7 | 636.6 | ||
| 0.82 | 2.9 | 4.3 | 7.0 | 9.9 | 31.6 | |
| 0.77 | 2.4 | 3.2 | 4.5 | 5.8 | 12.9 | |
| 0.74 | 2.1 | 2.8 | 3.7 | 4.6 | 8.6 | |
| 0.73 | 2.0 | 2.6 | 3.4 | 4.0 | 6.9 | |
| 0.72 | 1.9 | 2.4 | 3.1 | 3.7 | 6.0 | |
| 0.71 | 1.9 | 2.4 | 3.0 | 3.5 | 5.4 | |
| 0.71 | 1.9 | 2.3 | 2.9 | 3.4 | 5.0 | |
| 0.70 | 1.8 | 2.3 | 2.8 | 3.2 | 4.8 | |
| 0.69 | 1.7 | 2.1 | 2.5 | 2.8 | 3.8 | |
| 0.67 | 1.6 | 2.0 | 2.5 | 2.8 | 3.3 |
*здесь число степеней свободы f=n -1, где n – количество отсчетов.
|
|
|
