 |
Механические свойства материалов и методы их исследования
|
|
|
|
МЕХАНИЧЕСКИЕ СВОЙСТВА ТКАНЕЙ
1. Способы деформирования тел.
2. Механические свойства материалов и методы их исследования.
3. Механические свойства биологических тканей.
4. Механические модели.
Способы деформирования тел
Механическое воздействие на тело изменяет взаимное расположение его частиц.
Деформация - изменение взаимного расположения частиц тела, которое приводит к изменению его формы и размеров.
При действии на тело внешней деформирующей силы расстояние между частицами меняется. Это приводит к возникновению внутренних сил, стремящихся вернуть атомы (ионы) в первоначальное положение. Мерой этих сил является механическое напряжение.
Растяжение (сжатие)
Этот вид деформации возникает, когда к стержню (бруску) с закрепленным основанием прикладывается сила F, направленная вдоль его оси (рис. 1, а). Под действием этой силы длина стержня увеличивается на некоторую величину Δ l (l - первоначальная длина).
При этом в каждом сечении стержня возникают направленные по нормали силы (F1 и F2), равные по величине приложенной силе F и обусловленные изменением расстояния между частицами при растяжении. Сила F1 действует на верхнюю часть бруска со стороны нижней части; сила F2 - наоборот (рис. 1, б).
Состояние растянутого тела характеризуется продольным (нормальным) напряжением σ, которое может быть вычислено для любого сечения тела, перпендикулярного приложенной силе.

Рис. 6.1. Деформация растяжения (а); силы, возникающие при растяжении (б)
Нормальное напряжение равно отношению модуля силы, возникающей в данном сечении в результате растяжения, к площади сечения:

В СИ механическое напряжение измеряется в паскалях (Па).
|
|
|
Величина абсолютной деформации зависит от первоначальной длины стержня, поэтому степень деформации выражают через отношение абсолютной деформации к первоначальной длине. Это отношение называется относительной деформацией (ε):

Относительная деформация - величина безразмерная. Иногда ее выражают в процентах:
ε = (Δ l / l) 100%.
В большинстве случаев при растяжении или сжатии степень деформации в различных сечениях стержня различна. Это можно увидеть, если на поверхность тела нанести квадратную сетку. После деформирования сетка исказится. По характеру и величине этого искажения можно судить о распределении напряжения вдоль образца (рис. 2).
Видно, что изменения формы ячеек сетки максимальны в средней части стержня и почти отсутствуют на его краях.
Опытным путем было установлено, что небольшие деформации исчезают после снятия внешнего воздействия. Такие деформации называются упругими. Для них выполняется закон Гука:
При упругой деформации напряжение прямо пропорционально величине относительной деформации:

Коэффициент пропорциональности Е характеризует упругие свойства вещества при растяжении (сжатии) и называется модулем Юнга (модуль продольной упругости, Па).
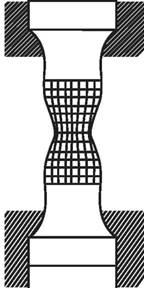
Рис. 2. Искажение квадратной сетки при растяжении стержня
Сдвиг
Деформация сдвига возникает, если на тело действует касательная сила, приложенная параллельно закрепленному основанию (рис. 3, а).
В этом случае направление смещения свободного основания параллельно приложенной силе и перпендикулярно боковой грани. В результате деформации сдвига
прямоугольный параллелепипед превращается в косоугольный. При этом боковые грани смещаются на некоторый угол γ, называемый углом сдвига.
При сдвиге в каждом сечении стержня возникают касательные силы (F1 и F2), равные по величине приложенной силе F и обусловленные изменением расстояния между частицами (рис. 3, б). Сила F1 действует на верхнюю часть бруска со стороны нижней части; сила F2 - наоборот.
|
|
|
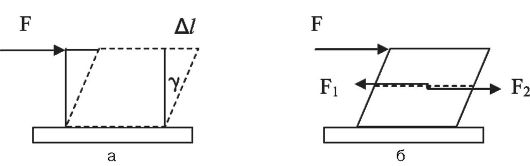
Рис. 3. Деформация сдвига (а); силы, возникающие при сдвиге (б)
Состояние тела при наличии деформации сдвига характеризуется касательным напряжением τ, которое может быть вычислено для любого сечения тела, параллельного закрепленному концу.
Касательное напряжение равно отношению модуля силы, возникающей в данном сечении в результате сдвига, к площади сечения:
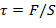
Абсолютная деформация сдвига измеряется величиной смещения свободного основания Δ l. Относительная деформация сдвига определяется через тангенс угла сдвига tgγ, называемый относительным сдвигом. Так как угол γ обычно мал, то можно считать tg(γ) ≈ γ.
При небольшой величине относительной деформации сдвига связь между деформацией и механическим напряжением выражается законом Гука:
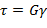
Коэффициент пропорциональности G характеризует упругие свойства вещества при сдвиге и называется модулем сдвига (Па).
Всестороннее сжатие
Если тело поместить в жидкую или газообразную среду, то на его поверхность будут действовать силы давления, перпендикулярные его поверхности. Эти силы вызовут сближение частиц тела, в результате чего произойдет уменьшение линейных размеров и объема тела. Такая деформация называется всесторонним или гидростатическим сжатием (рис. 4).
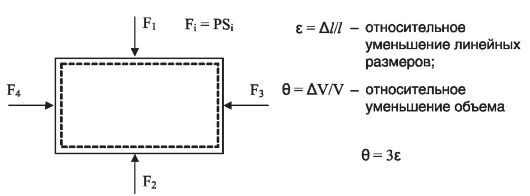
Рис. 4. Всестороннее (гидростатическое) сжатие
Относительная деформация при всестороннем сжатии характеризуется либо относительным уменьшением объема:

либо относительным уменьшением линейных размеров:

Механическое напряжение в этом случае равно давлению (Р), которое действует на поверхность тела. Связь между деформацией и напряжением выражается законом Гука:
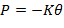
де K - модуль всестороннего сжатия (модуль объемного сжатия, объемный модуль). Знак «минус» означает, что объем уменьшается с увеличением напряжения.
Сжимаемость - важнейшая характеристика вещества, которая позволяет судить о зависимости физических свойств от межатомных (межмолекулярных) расстояний.
Изгиб
Этот вид деформации характеризуется искривлением оси или срединной поверхности деформируемого объекта (балка, стержень) под действием внешних сил (рис. 5).
|
|
|
При изгибе один наружный слой стержня сжимается, а другой наружный слой растягивается. Средний слой (называемый нейтральным) изменяет лишь свою форму, сохраняя длину (рис. 5, а). Степень деформирования бруска, имеющего две точки опоры (рис. 5, б), определяется по перемещению λ, которое получает его середина.
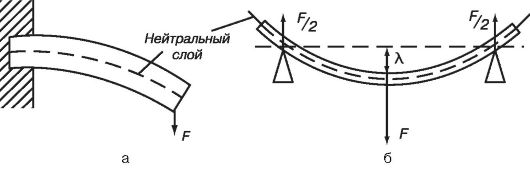
Рис. 5. Деформация изгиба:
а - стержень закреплен на одном конце; б - стержень опирается на две опоры
Величина λ называется стрелой прогиба. В теории сопротивления материалов показано, что стрела прогиба находится по формуле:
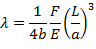
где F - сила; b - ширина; L - длина; a - толщина; E - модуль упругости.
Материал, находящийся в нейтральном слое, не работает, а лишь утяжеляет конструкцию. Поэтому часть вещества около этого нейтрального слоя можно удалить без большого ущерба для прочности балки, работающей на изгиб. Так добиваются уменьшения массы конструкции при сохранении заданной прочности. Например, сплошные брусья заменяют трубами, балки делают тавровыми или двутавровыми. Трубчатое строение имеют кости конечностей, стебли быстрорастущих растений-злаков и т.п.
Применительно к прямому брусу в зависимости от направления действующих сил изгиб называют продольным или поперечным.

Рис. 6. Различные виды изгиба:
а - продольный, б - поперечный, в - продольно-поперечный
Продольный изгиб возникает под действием сил, направленных вдоль бруса и приложенных к его концам навстречу друг другу (рис. 6, а). Образец приобретает форму арки. Поперечный изгиб возникает под действием сил, направленных перпендикулярно брусу и приложенных как к его концам, так и в средней части (рис. 6, б). Встречается также и смешанный продольно-поперечный изгиб (рис. 6, в).
Кручение
Этот вид деформации характеризуется взаимным поворотом поперечных сечений стержня под влиянием моментов (пар сил), действующих в плоскости этих сечений. Кручение возникает, например, когда нижнее основание стержня закреплено, а верхнее основание поворачивают вокруг продольной оси (рис. 7).
|
|
|
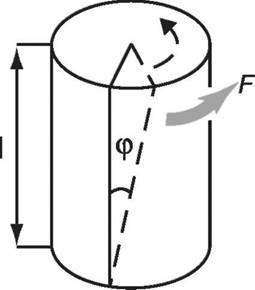
Рис. 7. Деформация кручения
При этом расстояние между различными слоями остается практически неизменным, но точки слоев, лежащие на одной вертикали, сдвинуты относительно друг друга. Этот сдвиг в разных местах будет различен. Например, в центре сдвига совсем не будет, по краям он будет максимальный.
Таким образом, деформация кручения сводится к неоднородному сдвигу.
Абсолютная деформация при кручении характеризуется углом поворота (φ) одного основания относительно другого.
Относительная деформация (θ) равна отношению угла φ к длине стержня l:

Сопротивление кручению очень быстро возрастает с увеличением радиуса, поэтому органы, рассчитанные на выполнение крутильных движений, как правило, длинные и тонкие (шея птиц, тело змеи).
Сравнивания различные способы деформирования однородных тел, можно увидеть, что все они сводятся к комбинации растяжения (сжатия) и сдвига.
Механические свойства материалов и методы их исследования
До сих пор мы рассматривали относительно небольшие деформации, для которых выполняется закон Гука. Рассмотрим теперь особенности, которые появляются при значительных величинах относительной деформации.
|
|
|


