 |
Повреждения трубчатых костей
|
|
|
|
Хрупкое разрушение характерно, например, для длинных трубчатых костей. Разрушения таких костей можно рассматривать как разрушения стержня при воздействии нагрузок в продольном или поперечном направлениях.
Продольные нагрузки (сжатие) возникают, например, при падении на кисть вытянутой руки, на руку, согнутую в локтевом суставе, или на согнутое колено (рис. 11).
Рис. 11. Повреждение нижнего эпифиза бедренной кости вследствие разрывных или сдвиговых деформаций возможно при падении на согнутое колено.
В спортивной практике часто имеет место повреждение костей вследствие их изгиба под влиянием внешнего воздействия. Зона начала разрушения диафиза длинной трубчатой кости при изгибе располагается на выпуклой стороне (рис. 12) дуги, где сосредоточиваются наибольшие значения растягивающих напряжений.
Другой вид повреждений больших трубчатых костей, сопровождающийся множественными переломами, возникает при ударе тупым предметом (рис. 13).
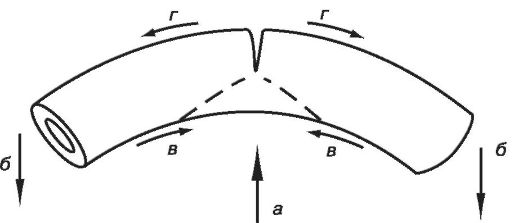
Рис. 12. Схема разрушения диафиза длинной трубчатой кости вследствие изгиба:
а, б - векторы внешних усилий, в - сжимающие, г - растягивающие усилия
Рис. 13. Схема механизма образования фрагментарного перелома диафиза длинной трубчатой кости с равномерным сечением (а) и с неравномерным сечением (б) при воздействии тупым предметом
Механические свойства биологических тканей
Структура материала является главным фактором, определяющим его механические свойства и характер процесса разрушения. Большинство биологических тканей являются анизотропными композиционными (от лат. - composition - сочетание) материалами, образованными объемным сочетанием химически разнородных компонентов. Состав каждого типа ткани сформировался в процессе эволюции и зависит от функций, которые она выполняет.
|
|
|
Костная ткань
Кость - основной материал опорно-двигательного аппарата. Так, в скелете человека более 200 костей. Скелет является опорой тела и способствует передвижению (отсюда и произошел термин «опорнодвигательный аппарат»). У взрослого человека скелет весит около 12 кг (18 % общего веса).
В компактной костной ткани половину объема составляет неорганический материал, минеральное вещество кости - гидроксилапатит. Это вещество представлено в форме микроскопических кристалликов. Другая часть объема состоит из органического материала, главным образом коллагена (высокомолекулярное соединение, волокнистый белок, обладающий высокой эластичностью). Способность кости к упругой деформации реализуется за счет минерального вещества, а ползучесть - за счет коллагена.
Кость является армированным композиционным материалом. Например, кости нижних конечностей армированы высокопрочными волокнами в окружных и спиральных перекрещивающихся направлениях.
Механические свойства костной ткани зависят от многих факторов: возраста, заболевания, индивидуальных условий роста. В норме плотность костной ткани 2400 кг/м3, а ее модуль Юнга Е = 1010 Па; предел прочности при растяжении σпр = 100 МПа, относительная деформация достигает 1%.
При различных способах деформирования (нагружения) кость ведет себя по-разному. Прочность на сжатие выше, чем на растяжение
или изгиб. Так, бедренная кость в продольном направлении выдерживает нагрузку 45 000 Н, а при изгибе - 2500 Н.
Запас механической прочности кости весьма значителен и заметно превышает нагрузки, с которыми она встречается в обычных жизненных условиях. (Живая кость в 5 раз прочнее железобетона.) Бедренная и берцовая кости выдерживают нагрузку в 25-30 раз больше веса нормального человека.
|
|
|
Особенность механического поведения костей состоит в том, что при их деформации проявляется пьезоэлектрический эффект. Если костную полоску, закрепленную на одном конце, изгибать, то в зоне деформации между противоположными сторонами регистрируется определенная разность потенциалов с отрицательным зарядом на вогнутой стороне (рис. 14).
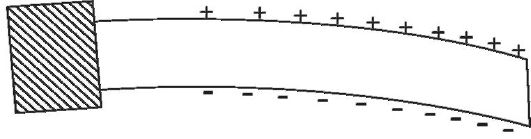
Рис. 14. Проявление пьезоэффекта при деформации костной полоски
В интервале упругой деформации эта разность потенциалов пропорциональна механическому напряжению.
Кожа
Кожа представляет собой не только совершенный покров тела, но является сложным органом, выполняющим важные функции: поддержание гомеостаза; участие в процессе терморегуляции, регуляцию общего обмена веществ в организме, секреторную функцию (работу сальных и потовых желез), защиту от повреждающего действия механических, физических, химических, инфекционных агентов. Она представляет собой обширное рецепторное поле, воспринимающее извне и передающее в ЦНС целый ряд ощущений. Кожа - граница раздела между телом и окружающей средой, поэтому она обладает значительной механической прочностью.
Кожа - самый крупный орган тела. Она - важная анатомо-физиологическая часть целостного организма. Функции кожи зависят от состояния всего организма. При различных заболеваниях, в том числе и внутренних органов, в коже происходят те или иные изменения.
Кожу часто рассматривают как гетерогенную ткань, состоящую из трех наложенных друг на друга слоев, которые тесно связаны между собой, но четко различаются по природе, структуре, свойствам: эпидермиса, дермы, подкожной клетчатки. Эпидермис покрыт сверху роговым слоем.
Функции каждого слоя кожи, в том числе и механические, отражают биомеханическую природу компонентов и их структурную организацию.
В общий состав кожи входят волокна коллагена, эластина и основной ткани - матрицы. Коллаген составляет 75 % сухой массы, а эластин - около 4 %. Плотность кожи в норме (область руки, груди) составляет 1100 кг/м3. Эластин растягивается очень сильно (до 200- 300 %). Коллаген может растягиваться до 10 %. Механические характеристики компонентов кожи:
• коллаген - Е = 10-100 МПа, σпр = 100 МПа;
• эластин - Е = 0,5 МПа, σпр = 5 МПа.
|
|
|
Кожа является вязкоупругим материалом с высокоэластичными свойствами, она хорошо растягивается и удлиняется.
При исследовании механических свойств кожи с помощью акустического анализатора тканей, позволяющего оценивать скорость распространения акустических возмущений звукового диапазона (5-6 кГц), была выявлена акустическая анизотропия кожи, которая проявляется в том, что скорости распространения поверхностной волны во взаимно перпендикулярных направлениях - вдоль вертикальной (У) и горизонтальной (Х) осей тела - различаются.
Сосудистая ткань
Механические свойства кровеносных сосудов определяются, главным образом, свойствами коллагена, эластина и гладких мышечных волокон. Содержание этих составляющих сосудистой ткани изменяется по ходу кровеносной системы. С удалением от сердца увеличивается доля гладких мышечных волокон, в артериолах они уже являются основной составляющей сосудистой ткани.
Так как стенки кровеносных сосудов построены из высокоэластичного материала, то они способны к значительным обратимым изменениям размера при действии на них деформирующей силы. Деформирующая сила создается избыточным внутренним давлением.
Рассмотрим деформацию сосуда как результат действия давления изнутри на упругий цилиндр. Имеется часть цилиндрического кровеносного сосуда длины L, с толщиной стенок h и внутренним радиусом r. Сечения вдоль и поперек оси цилиндра показаны на рис. 15.
Две половинки сосуда взаимодействуют между собой по сечениям стенок цилиндра (заштрихованные области на рис. 15, а). Общая площадь сечения, вдоль которого взаимодействуют обе половинки сосуда, равна 2hL. Если в сосудистой стенке существует механическое напряжение σ, то сила взаимодействия двух половинок равна
Эта сила уравновешивается силами избыточного давления Р на цилиндр изнутри (они показаны стрелками на рис. 15, б). Силы направлены под разными углами к горизонтальной плоскости. Для того чтобы найти их равнодействующую, следует просуммировать горизонтальные проекции.
|
|
|
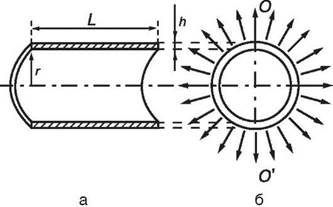
Рис. 16. Сечения цилиндрического сосуда вдоль оси (а) и поперек оси (б)
Однако проще найти равнодействующую силу, если умножить давление на проекцию площади полуцилиндра на вертикальную плоскость ОО'. Эта проекция равна 2rL. Тогда выражение для силы через избыточное давление имеет вид
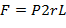
Приравняв уравнения, получим 
, откуда 
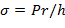
Это соотношение называется уравнением Ламе.
Механические модели
Вязкоупругие свойства тел (сочетание вязкого течения и высокой эластичности) моделируются системами, состоящими из различных комбинаций двух простых элементов: 1) пружины (упругий элемент) и 2) поршня с отверстиями, движущегося в цилиндре с вязкой жидкостью (вязкий элемент). Эти элементы и «конструируемые» с их помощью модели показаны на рис. 17 слева. Справа показаны зависимости деформации (ε) от времени при импульсном воздействии внешней силы: в момент времени t = 0 к телу, поведение которого моделируется, прикладывается постоянная сила F; в момент времени t1 действие силы прекращается.
Моделью упругого тела является пружина (рис. 17, а), подчиняющаяся закону Гука. Деформация (ε) мгновенно появляется в момент t = 0 и мгновенно исчезает в момент t1.
Рис. 17. Механические модели вязкоупругих тел и динамика развития деформации
Моделью вязкого тела является поршень с отверстиями, движущийся в цилиндре с вязкой жидкостью (рис. 17, б). Связь между скоростью деформации вязкой среды (скоростью перемещения поршня) и напряжением имеет вид
где 
– коэффициент вязкости среды, S – площадь поршня. Деформация нарастает линейно до некоторого значения, а после прекращения действия силы (момент 
) перестает изменяться.
Модель Максвелла
В модели Максвелла упругий и вязкий элементы соединены последовательно (рис. 17, в). Напряжение в каждом элементе является одинаковым. В любой момент времени для деформации выполняется условие
Скорость общей деформации равна:
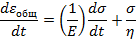
Решение этого уравнения приводит к следующему характеру развития деформации. В момент t = 0 пружина мгновенно растягивается, а затем начинается линейное нарастание деформации, связанное с движением поршня. В момент t1 пружина сокращается до начального размера, а поршень останавливается - имеет место остаточная деформация.
С помощью модели Максвелла можно моделировать следующие механические процессы.
Релаксация напряжения в материале: ε = const, dε/dt = 0, т.е. поддерживается постоянная деформация. В этом случае из уравнения следует:
Интегрируя последнее выражение от начального момента времени и начального напряжения σ о до текущих значений t иσ, получаем выражение, описывающее изменение напряжения со временем, т.е. релаксацию напряжения:
|
|
|
,
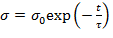где 
– время релаксации, за которое величина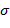 
уменьшается в е раз.
Ползучесть – изменение деформации при постоянном приложенном напряжении – 
. В этом случае 
и из уравнения следует, что 
или d 
. Интегрируя последнее выражение от начального момента времени и нулевой деформации до текущих значений t и 
, получаем выражение, описывающее изменение деформации со временем (ползучесть):
,
т.е. под действием постоянной приложенной силы происходит вязкое течение (поршень движется с постоянной скоростью).
При изучении свойств волос используют явление релаксации напряжения в них. Этот процесс аппроксимируют моделью, состоящей из 4 параллельно соединенных моделей Максвелла.
Модель Кельвина-Фойгта
Модель Максвелла не учитывает упругости, отличной от той, которая подчиняется закону Гука, т.е. упругости, возникающей за счет раскручивания макромолекул (высокоэластичности). Основной особенностью этого вида упругости является необходимость известного промежутка времени для ее развития (аналогия - деформация пружины в вязкой среде). Такая «запаздывающая» упругая реакция представляется моделью Кельвина-Фойгта, в которой пружина и поршень соединены параллельно (рис. 17, г). Величина удлинения одинакова для обоих элементов. При воздействии внешней силы общее напряжение равно сумме напряжений на каждом элементе:
Подставляя выражения для каждого элемента, получаем
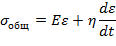
Деформация системы в момент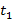 
(вывод опускаем) определяется формулой
При больших 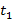экспонента стремится к 0. Поэтому деформация стремится к постоянному значению 
. После прекращения действия силы, деформация будет убывать постепенно до полного исчезновения по закону
, 
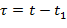
Модель Зинера
В материалах реализуются разные виды деформаций: упругая обратимая (модель - пружина), вязкоупругая обратимая (модель Кельвина-Фойгта) и необратимая (модель - поршень). Сочетание трех моделей, рассмотренных выше, позволяет создавать модели, наиболее полно отражающие механические свойства тел и, в частности, биологических объектов.
Примером такой модели является модель Зинера (рис. 17, д), которая состоит из последовательно соединенных упругого элемента и модели Кельвина-Фойгта. Временная зависимость относительной
деформации (без вывода) показана на рис. 17, д. При действии постоянной нагрузки мгновенно растягивается пружина 1, затем вытягивается поршень и растягивается пружина 2, после прекращения нагрузки происходит быстрое сжатие пружины 1, а пружина 2 втягивает поршень в прежнее положение; остаточная деформация отсутствует.
Поведение костной ткани в первом приближении описывается моделью Зинера. Упругая деформация реализуется за счет минерального вещества, а ползучесть - за счет коллагена.
|
|
|
