 |
Структурный анализ механизма
|
|
|
|
Введение
Основная цель курсового проектирования – привить навыки использования общих методов проектирования и исследования механизмов для создания конкретных машин и приборов разнообразного назначения. Студент должен научиться выполнять расчеты с использованием ЭВМ, применяя как аналитические, так и графические методы решения инженерных задач на разных этапах подготовки конструкторской документации.
Курсовое проектирование ставит задачи усвоения студентами определенных методик и навыков работы по следующим основным направлениям:
оценка соответствия структурной схемы механизма основным условиям работы машины или прибора;
проектирование структурной и кинематической схем рычажного механизма по заданным основным и дополнительным условиям;
анализ режима движения механизма при действии заданных сил; силовой анализ механизма с учетом геометрии масс звеньев;
учет сил трения в кинематических парах и определение коэффициента полезного действия;
проектирование зубчатых рядовых и планетарных механизмов;
расчет оптимальной геометрии зубчатых зацеплений; проектирование механизмов с прерывистым движением выходного звена;
разработка циклограмм и тактограмм для систем управления механизмами;
уравновешивание механизмов с целью уменьшения динамических нагрузок на фундамент и уменьшения сил в кинематических парах;
защита механизмов и машин от механических колебаний;
определение мощности и выбор типа двигателя.
Структурный анализ механизма
1.1 Определим степень подвижности механизма по формуле Чебышева
W = 3n – 2p5 – p4, (1.1)
|
|
|
где n = 3 – число подвижных звеньев механизма (1; 2; 3);
p5 = 4 – число кинематических пар V класса (1-2; 1- 4; 2-3; 3- 4).
С учётом этого
W = 3∙3 - 2∙4 = 1.
1.2 Примем в качестве ведущего звено 1. Отсоединяем от механизма наиболее удалённую от ведущего звена группу Асcура, состоящую из звеньев 2 и 3.
Рисунок 1.1 – Группа Ассура
1.3 Определяем степень подвижности W группы Ассура
W = 3∙2 - 2∙3 = 0.
где n = 2 - число подвижных звеньев механизма;
p5 = 3 – число кинематических пар V класса.
Определяем её класс, порядок, вид.
II класс, 2 порядок, 5 вид.
1.4 Определяем степень подвижности W ведущего звена 1
Рисунок 1.2 – Ведущее звено
W = 3∙1 - 2∙1 = 1, n = 1, p5 = 1
Определяем класс ведущего звена.
I класс
Структурный анализ выполнен правильно. Ведущие звенья относятся всегда к I классу.
Записываем формулу структурного строения механизма
I кл (1) + II кл (2;3). (1.2)
Т.к. в этой формуле наивысший класс группы Ассура II, то механизм относится ко II классу.
2 Кинематический анализ механизма методом планов
2.1 Исходные данные
ОА = 150 мм
ω1 = 30 рад/с
2.2 Переводим геометрические размеры звеньев механизма, заданные в мм, в метры, получим:
lOA = 0,15 м
2.3 Для построения восьми планов положения механизма назначаем масштаб механизма так, чтобы он занимал примерно формат А4.
(2.1)
где lOA = 0,15 м – истинный размер звена ОА в метрах;
ОА – отрезок, изображающий звено ОА в выбранном масштабе на чертеже, его длину назначаем произвольно. Примем ОА = 100 мм.
С учётом этого
.
2.4 Определяем отрезки, изображающие известные размеры звеньев механизма в выбранном масштабе на чертеже.
|
|
|
2.5 Построение восьми планов положения механизма будем вести от одного из крайних положений механизма. Примем за крайнее положение, то положение, когда звено ОА составляет с горизонталью угол 00.
2.5.1 В любом месте поля чертежа выбираем точку О.
2.5.2 От точки О откладывают отрезок ОА.
2.5.3 Из точки О проводим дугу окружности радиусом ОА.
2.5.4 На расстоянии е = 40 мм к верху от центра окружности проводим горизонтальную прямую длиной 360 мм.
2.5.5 Через точку А проводим прямую длиной 216 мм перпендикулярно ранее построенной. Получим механизм в крайнем правом положении.
2.5.6 Окружность радиуса ОА разбиваем на восемь равных частей от крайнего правого положения.
2.5.7 Проводим из точки О прямую до пересечения с окружностью. Обозначим точку пересечения А2. Получим механизм во втором положении.
Аналогично определяются другие положения звеньев механизма.
Рисунок 2.1 – План положений механизма
3 Кинематический анализ механизмов методом планов скоростей
3.1 Исходная схема механизма.
3.2 Т.к. звено 1 совершает вращательное движение, то линейную скорость точки А определим из соотношения
. (3.1)
VA ^ OA
Рисунок 3.1 – Исходная схема механизма
3.3 Т.к. звено 2 совершает плоскопараллельное движение, то для определения скорости точки В, принадлежащей второму звену, запишем теорему сложения скоростей
(3.2)
//хх ^ОА //уу
Из уравнения (3.2) можно определить два неизвестных параметра V А B и VA 3А2 путём построения плана скоростей. Построение плана скоростей будем вести по уравнению (3.2) в следующем порядке.
3.3.1 В любом месте поля чертежа выбираем полюс плана скоростей pV.
3.3.2 Из полюса pV откладываем отрезок pVa, изображающий скорость точки А перпендикулярно звену ОА. Длину отрезка pVa назначаем сами в пределах 50-100 мм. Примем pVa = 50 мм.
3.3.3 Через точку а на плане скоростей проводим линию действия вектора скорости 
// уу.
3.3.4 Через полюс pV проводим линию действия 
// хх. Точку пересечения проведенных выше линии обозначим через a 3.
|
|
|
3.3.5 Для определения численных значении скоростей определим масштаб полученного плана скоростей.
, (3.3)
где VA = 4,5 м/с – скорость точки А, м/с;
pV a = 50 мм – отрезок, изображающий скорость точки А на плане скоростей, мм.
С учётом этого
Численные значения найденных скоростей будут равны
;
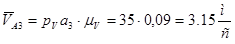Аналогично строятся планы скоростей для оставшихся семи положений механизма. Результаты расчётов сведём в таблицу 3.1.
Таблица 3.1 – Скорости точек звеньев механизма
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| VA 1 | 4,5 | 4,5 | 4,5 | 4,5 | 4,5 | 4,5 | 4,5 | 4,5 |
| V А3 | 0 | 3,15 | 4,5 | 3,15 | 0 | 3,15 | 4,15 | 3,15 |
| V А3А2 | 0 | 3,15 | 4,5 | 3,15 | 0 | 3,15 | 4,15 | 3,15 |
4. Кинематический анализ механизмов методом планов ускорений
4.1 Исходная кинематическая схема механизма
Рисунок 4.1 - Исходная кинематическая схема механизма
4.2 Определим линейное ускорение точки А, принадлежащей звену 1. Т.к. звено совершает вращательное движение, то ускорение точки А будет складываться из следующих составляющих
, т. к e1 = 0, то 
.
С учётом этого
;
; (4.1)
4.3 Для определения ускорения точки А3 запишем теорему сложения ускорении
(4.2)
// ОА // ВА // уу
4.4 Для построения плана ускорении по уравнению (4.2) назначим масштаб будущего плана ускорении
, (4.3)
где 
, нормальное ускорение точки А2;
- отрезок, изображающий ускорение точки А2 на чертеже. Его длину выбираем произвольно (50-100 мм). Примем 
=50 мм.
|
|
|
С учётом этого
.
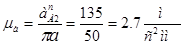4.5 Построение плана ускорении будем вести по уравнению (4.2)
Рисунок 4.2 - План ускорений механизма в 6-ом положении.
4.5.1 В любом месте поля чертежа выбираем полюс плана ускорении p.
4.5.2 Из полюса p откладываем отрезок p = 50 мм параллельно звену ОА.
4.5.3 Из конца вектора ускорения точки А2 (точка а1) проводим линию действия ускорения А3А2 параллельно уу.
4.5.4 Из полюса p проводим линию действия ускорения А3 параллельно уу.
4.5.5 Точку пересечения проведённых выше линии обозначим а3.
4.6.8 Определим численное значение найденных ускорений.
;
;
;
Силовой расчёт механизма
5.1 Исходная схема механизма
Рисунок 5.1 - Исходная схема механизма
5.2 Определяем массу звеньев механизма, используя исходные данные
, (5.1)
где g = удельная масса звена, кг/м;
li – длина соответствующего звена, м.
С учётом этого
5.3 Определяем вес звеньев механизма
(5.2)
где 
- масса i – звена, кг;
g – ускорение свободного падения, м/с2
5.4 Определим инерциальные нагрузки, действующие на все звенья механизма
(5.3)
где 
- ускорение центра масс i – звена, м/с2.
5.5 Силовой расчёт механизма начинаем с наиболее удалённой от ведущего звена группы Ассура. В нашем случае группой Ассура является группа, состоящая из звеньев 2 и 3. Отсоединим её от основного механизма. Вычерчиваем отдельно в таком же положении, в таком же масштабе как было на механизме.
Рисунок 5.2 – Силовой расчет группы Ассура
5.6 На выделенную группу Ассура наносим все действующие силы: внешние (Gi, F и i) и внутренние (N 1, N 2).
5.7 Неизвестные реакции определим графическим путем по следующему векторному уравнению
(5.4)
Для построения плана сил по записанному уравнению выберем масштаб построения
; (5.5)
где Fma x – максимальная по величине сила в уравнении, Н;
оа – отрезок, изображающий максимальную силу на чертеже, его длину назначаем сами не менее 100 мм.
С учётом этого
.
Определим отрезки, изображающие известные силы в выбранном масштабе
;
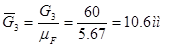5.8 Построение плана сил по написанному выше уравнению ведём в следующем порядке
|
|
|
Рисунок 5.3 – План сил группы Ассура
5.8.1 В любом месте поля чертежа откладываем отрезок, изображающий силу 
.
5.8.2 Из конца этого вектора откладываем отрезок, изображающий силу 
.
5.8.3 Из конца вектора 
проводим линию действия силы 
.
5.8.4 Из конца вектора проводим линию действия силы 
.
5.8.5 Из начала вектора 
проводим линию действия силы.
5.9 Определяем численное значение найденных реакции, используя план сил
;
.
5.10 Расчёт ведущего звена механизма.
5.10.1 Вычерчиваем ведущее звено отдельно от механизма в заданном положении и в заданном масштабе (рис. 5)
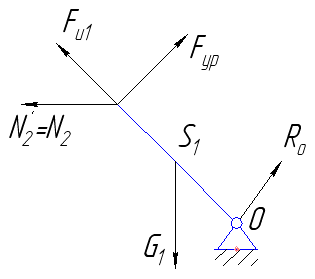
Рисунок 5.4 – силовой расчет ведущего звена
На ведущее звено наносим все действующие силы: 
, 
, 
, 
.
5.10.2 Определяем уравновешивающую силу из условия равновесия звена ОА аналитически
(5.6)
5.13 Для определения реакции в точке О построим план сил для ведущего звена по следующему векторному уравнению
(5.7)
Назначаем масштаб построения
Рисунок 5.5 – план сил ведущего звена
Определяем отрезки, изображающие силы в выбранном масштабе
;
;
;
.
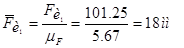Рычаг Жуковского
6.1 Для исходного положения механизма поворачиваем план скоростей на 90° в любую сторону.
6.2 К повёрнутому плану скоростей в соответствующих точках прикладываем все внешние силы и моменты (
, 
и т.д.)
6.3 К точке a 1 плана скоростей прикладываем уравновешивающую силу F ур ^ pva 1
Рисунок 6.1 – Рычаг Жуковского Н.Е.
6.4 Из условия равновесия повёрнутого плана скоростей определяется F ур по величине и направлению
(6.1)
С учётом этого
Расхождение F ур, найдённой при расчёте ведущего звена и с помощью рычага Жуковского должно составлять не более 10 %.
Следовательно, силовой анализ механизма выполнен правильно.
7 Синтез планетарных передач
7.1 Исходные данные: n1 = 655 об/мин, nдв = 2940 об/мин, m = 3 мм
7.2 Определим передаточное отношение привода
(7.1)
7.3 Записываем условие постоянства передаточных отношений для исходной схемы редуктора
=> 
(7.2)
Полученное значение округлили до целого, при этом Z1 = 87
7.4 Определим число зубьев сателлита из условия соосности:
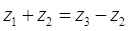(7.3)
7.5 Проверим условие соседства сателлитов, при условии к=3
> 
(7.4)
> 31+2
7.6 Примем условия сборки планетарного редуктора
(7.5)
|
|
|
