 |
Сопротивление растяжению жидкостей
|
|
|
|
Сопротивление растяжению жидкостей заключается в способности жидкости противостоять растягивающим силам.
Сопротивление растяжению жидкостейможет возникать только в дегазированных жидкостях. В опытах удавалось при центрифугировании дегазированной дистиллированной воды получить на очень короткое время напряжения растяжения в воде, доходившие приблизительно до 25 МПа. Технические жидкости не сопротивляются растягивающим усилиям.
Газы могут находиться в жидкости в растворенном и нерастворенном виде. Присутствие в жидкости нерастворенного газа в виде пузырьков существенно уменьшает модуль упругости жидкости, причем это уменьшение не зависит от размеров пузырьков воздуха. Динамическая вязкость жидкости с увеличением содержания в ней воздуха растет. Содержание нерастворенного воздуха в рабочих жидкостях гидросистем машин и механизмов, так же как и в трубопроводах, подающих жидкость, может сильно повлиять на параметры работы трубопроводов и гидросистем.
Вязкость
Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу ее слоев. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения, или силами вязкости. Если рассмотреть то, как распределяются скорости различных слоёв жидкости по сечению потока, то можно легко заметить, что чем дальше от стенок потока, тем скорость движения частиц больше. У стенок потока скорость движения жидкости равна нулю. Иллюстрацией этого является рисунок, так называемой, струйной модели потока. На рисунке применены следующие обозначения:
|
|
|
- скорость слоя жидкости,
- расстояние между соседними слоями жидкости.
Медленно движущийся слой жидкости «тормозит» соседний слой жидкости, движущийся быстрее, и наоборот, слой, движущийся с большей скоростью, увлекает (тянет) за собой слой, движущийся с меньшей скоростью. Силы внутреннего трения появляются вследствие наличия межмолекулярных связей между движущимися слоями.
Закон жидкостного трения – закон Ньютона
Если в равномерно движущемся потоке жидкости рассмотреть два соседних слоя с ординатами y1 и y2, расположенных на расстоянии dy друг от друга, и скорость первого из них обозначить u1, а скорость другого u2, то разница между ними составит du. Тогда можно записать
Эта величина называется градиентом скорости по сечению потока или поперечным градиентом скорости. Он показывает, как меняются скорости слоёв жидкости по сечению потока.
Если между соседними слоями жидкости выделить некоторую площадку S, то согласно гипотезе Ньютона
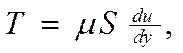
где T – силы вязкого трения;
S – площадь трения;
μ – коэффициент вязкого трения.
Величина μ в этом выражении является динамическим коэффициентом вязкости, равным
или
;
где τ – касательное напряжение в жидкости (зависит от рода жидкости).
Физический смысл коэффициента вязкого трения - число, равное силе трения, развивающейся на единичной поверхности при единичном градиенте скорости.
Единицы измерения: [Н·с/м2], [кГс·с/м2], [Пз]{Пуазейль}, 1Пз=0,1Н·с/м2.
На практике чаще используется кинематический коэффициент вязкости, названный так потому, что в его размерности отсутствует обозначение силы. Этот коэффициент представляет собой отношение динамического коэффициента вязкости жидкости к её плотности
.
Единицы измерения: [м2/c], [cм2/c], [Ст] {стокс}, [сСт] {сантистокс}, 1Ст=100сСт {1Ст=1 cм2/c}.
Анализ свойства вязкости
Для капельных жидкостей вязкость зависит от температуры t и давления Р, однако последняя зависимость проявляется только при больших изменениях давления, порядка нескольких десятков МПа.
|
|
|
Зависимость коэффициента динамической вязкости от температуры выражается формулой вида:
где μt – коэффициент динамической вязкости при заданной температуре,
μ0 – коэффициент динамической вязкости при известной температуре (для минеральных масел при 50 0C),
T – заданная температура,
T0 –температура, при которой измерено значение μ0 (50 0C для минеральных масел),
kt – коэффициент, для минеральных масел равный 0,02-0,03,
e – основание натурального логарифма равное 2,718282.
Зависимость относительного коэффициента динамической вязкости 
от давления описывается формулой
где μP – коэффициент динамической вязкости при заданном давлении,
μ0 – коэффициент динамической вязкости при известном давлении (чаще всего при нормальных условиях),
P – заданное давление,
P0 –давление, при которой измерено значение μ0 ,
kP – коэффициент, для минеральных масел равный 0,002-0,003.
Влияние давления на вязкость жидкости проявляется только при высоких давлениях.
Для примера приведём значения кинематического коэффициента вязкости n для некоторых жидкостей: масла индустриальные (по ГОСТ 20799-75) при температурах 50 0C: И-5А – 4-5 сСт, И-12А – 10-14 сСт, И-40А – 35-45 сСт; вода пресная при 20 0C - 0,0101Ст; ртуть при 150C 0,0011- Ст, сталь жидкая при 1550 0C– 0,0037 Ст.
Вязкость жидкости - это свойство, проявляющееся только при движении жидкости, и не влияющее на покоящиеся жидкости. Вязкое трение в жидкостях подчиняется закону трения, принципиально отличному от закона трения твёрдых тел, т.к. зависит от площади трения и скорости движения жидкости.
Жидкости, которые подчиняются описанному закону жидкостного трения Ньютона, называются ньютоновскими жидкостями. Однако есть жидкости, трение в которых описывается другими закономерностями.
Неньютоновские жидкости
Особенностью ньютоновских жидкостей является полное отсутствие трения покоя. Однако существуют жидкости (растворы полимеров, коллоидные суспензии, строительные растворы, пищевые и кормовые смеси и т. п.), для которых связь между касательным напряжением t и поперечным градиентом скорости не подчиняется закону Ньютона. Такие жидкости называются неньютоновскими или аномальными, и отличаются от ньютоновских наличием касательного напряжения в состоянии покоя t0.
|
|
|
Например, касательные напряжения подчиняются закону
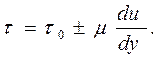
Такие жидкости называются вязкопластичными, и движение их слоёв начинается лишь после того, как будет преодолено напряжение сдвига покояt0.
Для других неньютоновских жидкостей динамическая вязкость может зависеть от градиента скорости, времени и т. д. Эта зависимость может иметь, например, следующий вид
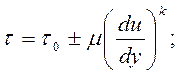
где k – коэффициент, который может зависеть от скорости, времени, температуры, давления и некоторых других факторов.
|
|
|
