 |
Свойства гидростатического давления
|
|
|
|
Первое свойство формулируется следующим образом: на внешней поверхности жидкости гидростатическое давление всегда направлено по нормали внутрь рассматриваемого объёма.
В приведённой формулировке «внешняя поверхность» это любая поверхность, которую можно выделить внутри жидкости (даже мысленно), или поверхность раздела сред.
Доказывается первое свойство путём рассуждений методом «от противного».
Рассмотрим покоящуюся жидкость. Известно, что жидкость плохо сопротивляется касательным усилиям. Если бы сила, от давления R действовала бы не по нормали к площадке, то её можно было бы представить в виде двух составляющих – нормальной Fn и касательной Fτ. Тогда касательная составляющая смещала бы слои жидкости друг относительно друга. Это означало бы, что жидкость не находилась бы в покое. Это противоречит начальному утверждению.
Из первого свойства следует, что напряжение сжатия - единственный вид напряжений в покоящейся жидкости
Второе свойство состоит в том, что в любой точке внутри жидкости давление по всем направлениям одинаково. Иначе это свойство давления звучит так: на любую площадку внутри объёма жидкости, независимо от её угла наклона, действует одинаковое давление.
Докажем второе свойство. Для этого рассмотрим произвольный объём в неподвижной жидкости в виде прямоугольного тетраэдра с размерами 
. Будем рассматривать этот объём в некоторой произвольной системе координат X, Y, Z.
На рисунке приведены следующие буквенные обозначения:
- гидростатическое давление, действующее на грань, перпендикулярную соответствующей оси,
- гидростатическое давление, действующее на наклонную грань dS,
F - инерционные силы (или силы веса).
|
|
|
Тетраэдр dx, dy, dz по определению находится в покое, следовательно, сумма сил, действующих на него равна 0, т.е.
Подробно рассмотрим эти силы. Прежде всего, на выделенный тетраэдр действуют силы давления. В проекциях на оси системы координат по направлению каждой из осей действует сила от давления на грань, перпендикулярную этой оси. Этой силе противодействует проекция на соответствующую ось силы давления на наклонную (большую) грань тетраэдра. Получаются три пары сил, соответственно осям:
Вместе с силами давления, в общем случае, на тетраэдр действуют инерционные силы (или в простейшем случае сила веса), которые равны произведению массы на проекцию ускорения на соответствующую ось. Массу определим как произведение плотности жидкости и объёма тетраэдра. Объём для прямоугольного тетраэдра равен 
. В этом случае инерционные силы примут вид:
.
Сложив обе полученные системы уравнений, и, приравняв их 0 по причине равновесия тетраэдра, получим общую систему уравнений сил, действующих в покоящейся жидкости:
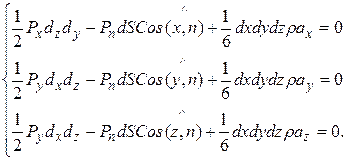
Если учесть, что площадь каждой грани тетраэдра, параллельной плоскостям координат, равна площади проекции наклонной грани на соответствующую координатную плоскость, получим следующее равенство:
.
Разделив уравнения сил на соответствующие одинаковые площади, получим:
.
Устремив размеры тетраэдра к 0, т.е. 
и 
последняя система уравнений примет вид:
.
Приравняв все три уравнения, получим следующее равенство:
.
В результате можно сделать следующий вывод: давление не зависит от направления, или другими словами: давление - величина скалярная.
Однако возникает вопрос, каким образом получается, что давление и площадь величины скалярные, а их произведение сила – величина векторная.
.
Ответ на этот вопрос заключается в следующем. Направление векторасилы задаёт площадка, на которую действует давление. Это направление всегда перпендикулярно площадке действия и направлено внутрь рассматриваемого объёма.
|
|
|
|
|
|
