 |
Билет №23 Базис, координаты вектора, размерность пространства.
|
|
|
|
Билет 59
Поле комплексных чисел, комплексные числа в алгебраической, тригонометрической, показательной формах.
i – мнимая единица
Комплексными называются числа вида z=x+iy
x=R z - действительная часть
iy=Im z – мнимая часть действительных чисел
а = 5
a=5+0i
Между комплексными числами и точками плоскости существует взаимно однозначное соответствие.
z=x+iy алгебраическая форма комплексных чисел
z=x-iy Сопряженное комплексное число
Степени мнимой единицы.
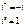
Пример. 
Тригонометрическаяформа
z=x+y
- Тригонометрическая форма
Показательная форма
Билет 58
Теорема Безу, основная теорема алгебры
Теорема Безу
Остаток от деления многочлена 
на двучлен 
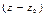равен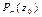 
Доказательство:
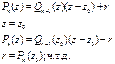
Следствие:
Для того, чтобы Pn(z) делился на 
без остатка, необходимо и достаточно чтобы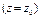 
было корнем многочлена.
Основная теорема алгебры (Гауса):
Всякий многочлен Pn(z) степени не меньше 1 (n>=1) имеет по крайней мере 1-н корень
Доказательство:
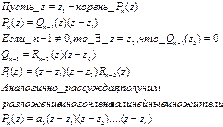
Билет 59
Понятие числового поля, аксиомы поля
Множества натуральных чисел N={0;1;2;3;4;5;6;7;8….;n,…}
Множества целых чисел Z={ 
}
Множества рациональных чисел
I – Множество иррациональных чисел (бесконечная, непериодическая дробь).
Множество действительных чисел R=Q U I
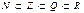
Всякая система чисел, содержащая сумму, разность и произведение 2-х своих чисел, называется кольцом
Z; Q; R; C – числовые кольца
N – Не является кольцом
Числовое кольцо называется числовым полем, если оно содержит честное 2-х своих чисел (делитель не равен нулю).
Q; R; C – числовые поля
I – не является числовым полем
Числовое поле <P+;*> P – носитель числового поля
|
|
|
Существуют a; b; c принадлежащие P
Выполняется 9-ть аксиом:
1) a+b=b+a коммутативность
2) (a+b)+c=a+(b+c) ассоциативность
3)Пусть существует 0 принадлежащий P, для любого a принадлежащего P => а+0=а (существование нулевого элемента).
4)Для любого а принадлежащего Р, существует (-а) принадлежащее Р => а+(-а)=0 (существование противоположного элемента).
5) a*b=b*a коммутативность умножения
6) (a*b)*c=a*(b*c) ассоциативность умножения
7) существует 1 принадлежащий P, для любого 0 принадлежащего P => а*1=1*а=а (существование единичного элемента).
8) 
9) (a+b)*c=a*c+b*c дистрибутивность
Билет 55, 56
Понятие линейного и векторного пространства, критерий подпространства
Линейные пространства!
Пусть L-некоторое множество, элементы которого мы будем называть «векторами», |Р – некоторое числовое поле. Пусть также выполнены следующие условия:
1)В L определена операция «сложения» элементов, то есть для любого х,у принадлежащих L становится в соответствие элемент z принадлежащий L. Обозначают 
.Эта операция обладает следующими свойствами:
2)в L определена операция «умножения» элемента на число из |Р, то есть для любого λ принадлежащего |Р, для любого х принадлежащего L ставится в соответствии элемент y принадлежащий L. Обозначается 
. Это операция обладает свойствами 
3)эти операции удовлетворяют законам дистрибутивности:
\
Все эти свойства называются аксиомами пространства.
Пространство L называется действительным, если |P=|R и операция умножения вектора на число определена только для действительных чисел, и комплексным, если |P=C и эта операция определена для комплексных чисел.
Подмножество V линейного пространства L называется линейным подпространством, если V само является линейным подпространством относительно операций, определенных на L.
Критерий подпространства
Векторное пространство
Множество геометрических векторов в совокупности с введенными в предыдущем разделе линейными операциями над ними будем называть пространством геометрических векторов.
|
|
|
Три пространства векторов: 
Множество L называется линейным векторным пространством над полем скаляров К если для любых элементов 
Элементами ЛВП могут быть объекты любой природы, их принято называть векторами.
Элементами числового поля являются скалярные числа.
Билет №23 Базис, координаты вектора, размерность пространства.
Упорядоченная система из n элементов 
называется n-мерным вектором.
Множество Ln называется n-мерным линейным пространством над полем скаляров R, если 
определена операция сложения 
и операция умножения на число 
при выполнении 8 аксиом ЛП.
Если n-размерность пространства Ln, то это значит, существует в Ln n линейно независимых векторов, а любые (n+1) векторов являются линейно зависимыми.
Базис пространства Vn– максимальная по включению линейно независимая система векторов из Vn
Таким образом, если 
- базис пространства Vn
1)то вектора { 
} образуют линейно независимую систему
В каждом пространстве геометрических векторов существует множество различных базисов, но они все состоят из одного и того же числа векторов. Число векторов в базисе пространства называется размерностью этого пространства.
Любой вектор х принадлежащий L может быть разложен по базису, то есть представлен в виде линейной комбинации базисных векторов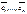 
и при том единственным образом 
Коэффициенты этого разложения x1,…,xn называется координатами вектора х в базисе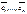
Билет №26
|
|
|
