Главная | Обратная связь | Поможем написать вашу работу!

Оценивание выражений

Встречая выражение, Maple 7 оценивает его, то есть устанавливает возможность его вычисления. Если выражение — скалярная переменная, то ее значение будет выведено в ячейке вывода. Для переменных более сложных типов выводится не их значение, а просто повторяется имя переменной. Просто повторяются также имена неопределенных переменных.

Для оценивания выражений различного типа существует группа функций, основные из которых перечислены ниже:

eval (array) — возвращает вычисленное содержимое массива array;
evalf(expr, n) — вычисляет ехрr и возвращает вычисленное значение в форме числа с плавающей точкой, имеющего n цифр после десятичной точки;
eval hf(ехрг) — вычисляет ехрг и возвращает вычисленное значение с точностью, присущей оборудованию данного компьютера;
evalf(int(f, x=a..b)) — оценивает и возвращает значение определенного интеграла int(f,x=a..b);
evalf(Int(f, x=a..b)) — оценивает и возвращает значение определенного интеграла, заданного инертной функцией Int(f,x=a..b);
evalf(Int(f. x=a..b, digits, flag)) — аналогично предыдущему, но возвращает значение интеграла с заданным параметром digits числом цифр после десятичной точки и со спецификацией метода вычислений flag;
evalm(mexpr) — вычисляет значение матричного выражения mexpr и возвращает его;
evalb(bexpr) — вычисляет и возвращает значения логических условий;
evalc(cexpr) — вычисляет значение комплексного выражения;
evalr (ехрr, ampl) — оценивает и возвращает значения интервальных выражений (функция должна вызываться из библиотеки);
shake(expr, ampl) — вычисляет интервальное выражение.

Для функции evalf параметр n является необязательным, при его отсутствии полагается n=10, то есть вещественные числа выводятся с мантиссой, имеющей десять цифр после десятичной запятой.

В выражении ехрr могут использоваться константы, например Pi, exp(l), и функции, такие как ехр, 1 n, arctan, cosh, GAMMA и erf. В матричном выражении mexpr для функции evalr могут использоваться операнды в виде матриц и матричные операторы &*, +, - и ^. В комплексных выражениях mexpr наряду с комплексными операндами вида (а + I*b) могут использоваться многие обычные математические функции:

sin	cos	tan	CSC	sec	cot
sinh	cosh	tanh	csch	sech	coth
arcsin	arccos	arctan	arccsc	arcsec	arccot
arcsinh	arccosh	arctanh	arccsch	arcsech	arccoth
exp	In	•sqrt	*	abs	conjugate
polar	argument	signura	csgn	Re	Im
Ei	LambertW	dilog	surd

Примеры применения функций оценивания даны ниже:

В дальнейшем мы многократно будем применять функции оценивания для демонстрации тех или иных вычислений.

Gif

Последовательности выражений.

Последовательности выражений

Maple 7 может работать не только с одиночными выражениями, но и с последовательностями выражений. Последовательность выражений — это ряд выражений, разделенных запятыми и завершенных фиксатором:

Для автоматического формирования последовательности выражений применим специальный оператор $, после которого можно указать число выражений или задать диапазон формирования выражений:

Для создания последовательностей выражений можно использовать также функцию seq:

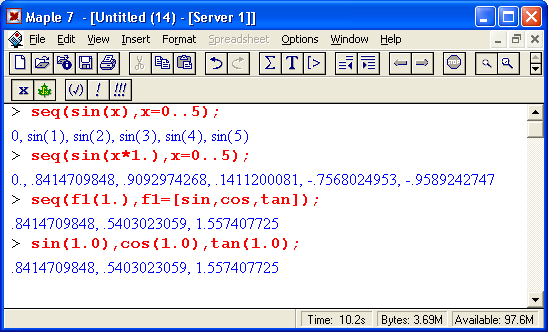
Gif

Вывод выражений

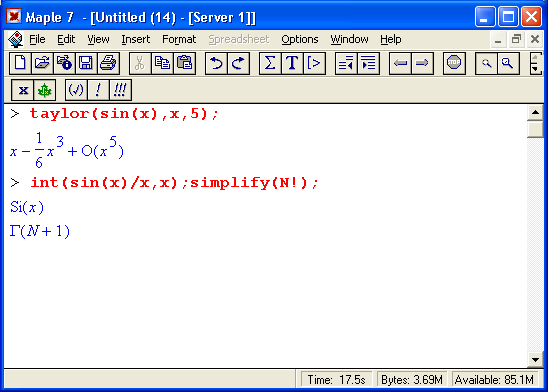
При выполнении порой даже простых операций результаты получаются чрезвычайно громоздкими. Для повышения наглядности выражений Maple 7 выводит их с выделением общих частей выражений и с присваиванием им соответствующих меток. Метки представлены символами #N, где N — номер метки. Помимо меток при выводе результатов вычислений могут появляться и другие специальные объекты вывода, например корни RootOf, члены вида О(х"), учитывающие погрешность при разложении функций в ряд, и обозначения различных специальных функций, таких как интегральный синус, гамма-функция и др. Примеры такого вывода приведены ниже:

Часто встречаются также знаки ~ для отметки предполагаемых переменных, постоянные интегрирования и другие специальные обозначения. По мере упоминания в тексте таких объектов вывода они будут описаны.

Gif

Простые типы данных

Числа и числовые константы

Maple 7 работает с числами следующего типа: целыми (О, 1, 123, -456 и т. д.), рациональными в виде отношения целых чисел (7/9, -123/127 и т. д.), вещественными с мантиссой и порядком (1.23Е5, 123.4567Е-10). Признаком вещественного числа является десятичная точка (запятая). Примеры простых операций с числами приведены ниже:

Как видно из этих примеров, ввод и вывод чисел имеет следующие особенности:

для отделения целой части мантиссы от дробной используется разделительная точка;
нулевая мантисса не отображается (число начинается с разделительной точки);
мантисса отделятся от порядка пробелом, который рассматривается как знак умножения;
мнимая часть комплексных чисел задается умножением ее на символ мнимой единицы I (квадратный корень из -1).

Десятичная точка в числах имеет особый статус — указание ее в любом месте числа, даже в конце, делает число вещественным и ведет к переводу вычислений в режим работы с вещественными числами. При этом количеством выводимых после десятичной точки цифр можно управлять, задавая значение системной переменной окружения Digits:

Для работы с числами Maple 7 имеет множество функций. Они будут рассмотрены в дальнейшем. На комплексной плоскости числа задаются координатами точек (х, у) (рис. 5.1).

Рис. 5.1. Представление обычных и комплексных чисел на плоскости

Для представления чисел на рис. 5.1 используется функция pointplot(list), где list — список координат точек. Эта функция становится доступной при подключении пакета plots командой with(plots). Кроме того, использована функция вывода ряда графических объектов на один график — display (см. далее описание представления комплексных чисел).

С помощью функции convert Maple 7 может преобразовывать числа с различным основанием (от 2 до 36, в том числе бинарные и шестнадцатеричные) в десятичные числа:

При символьных вычислениях Maple 7 реализует точную арифметику. Это значит, что результат может быть получен с любым числом цифр. Однако надо помнить, что идеально точные численные вычисления выполняются только в случае целочисленных операций, например таких, как приведены ниже:

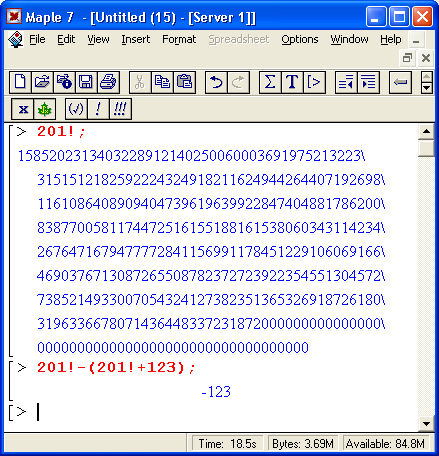
Gif

Комплексные числа

Maple 7, естественно, может работать с комплексными числами. Мнимая единица в комплексном числе (корень квадратный из -1) обозначается как I. Функции Re(x) и Im(x) возвращают действительную и мнимую части комплексных чисел. Примеры задания комплексного числа и вывода его действительной и мнимой частей представлены ниже:

Комплексные числа обычно представляют на так называемой комплексной плоскости, у точек которой координата х задает действительную часть комплексного числа, а у (мнимая ось) показывает мнимую часть такого числа. На рис. 5.1 показано задание в виде радиус-векторов комплексного числа z = 4+3I, -z и комплексно-сопряженного числа 4-3I.

Окружность радиуса abs(z)=sqrt(a2 + b2) представляет абсолютное значение комплексного числа z=a+b*I. Она является геометрическим множеством комплексных чисел, образованных концом вращающегося радиус-вектора числа z вокруг его начала в точке (0, 0) комплексной плоскости. Позже мы рассмотрим ряд функций для работы с комплексными числами.

Gif

Контроль за числами

Числа могут служить объектами ввода, вывода и константами, входящими в математические выражения. Функция type(x, numeric) позволяет выяснить, является ли х числом. Если является, то она возвращает логическое значение true (истина), а если нет, то false (ложь). Например:

Функции type(x, integer), type(x, rational) и type(x, fraction) можно использовать для проверки того, имеет ли х значение соответственно целого числа, рационального числа или простой дроби:

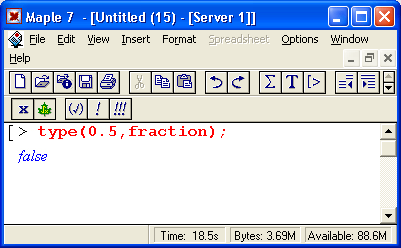
Gif

⇐ Предыдущая 18 19 20 21 222324 25 26 27 Следующая ⇒

Воспользуйтесь поиском по сайту: