 |
Основной способ задания функции пользователя
|
|
|
|
Более гибкий способ задания полноценных функций пользователя базируется на применении функционального оператора. При этом используется следующая конструкция:
name:=(x,y,...)->expr
После этого вызов функции осуществляется в виде name(x.y,...), где (х.у,...) — список формальных параметров функции пользователя с именем name. Переменные, указанные в списке формальных параметров, являются локальными. При подстановке на их место фактических параметров они сохраняют их значения только в теле функции (ехрr). За пределами этой функции переменные с этими. именами оказываются либо неопределенными, либо сохраняют ранее присвоенные им значения. Следующие примеры иллюстрируют сказанное:

Нетрудно заметить, что при вычислении функции m(х.у) переменные х и у имели значения 3 и 4, однако за пределами функции они сохраняют нулевые значения, заданные им перед введением определения функции пользователя. Еще один способ задания функции пользователя базируется на применении функции unapply: name:=unapply(expr.varl.var2,...) Ниже даны примеры такого задания функции пользователя:
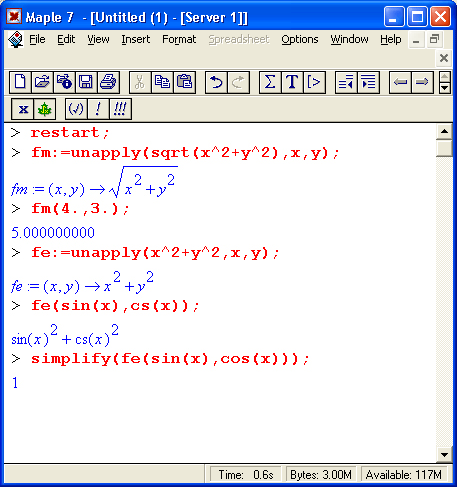
Последний пример показывает возможность проведения символьных операций с функцией пользователя.
Gif

Gif

Графическая визуализация результатов выполнения функций пользователя
Графическая визуализация результатов выполнения функций пользователя
В ряде случаев весьма желательна визуализация результатов выполнения функций пользователя. Порой она может давать неожиданный результат. На рис. 7.1 представлены примеры задания двух функций пользователя от двух переменных и построение их графиков с помощью функции plot3d.

а

б
Рис. 7.1. Примеры задания функций пользователя двух переменных с построением их графиков
|
|
|
ВНИМАНИЕ
При задании функций пользователя рекомендуется просмотреть их графики в нужном — диапазоне изменения аргументов. К сожалению, наглядными являются только графики функций одной и двух переменных.
Gif

Gif

Импликативные функции
Импликативные функции
Другой важный класс функций, которые нередко приходится задавать, — импликативные функции, в которых связь между переменными задана неявно, в виде какого-либо выражения. Самый характерный пример такой функции — это выражение для задания окружности радиуса r: х^2 + у^2 = r^2.
Итак, импликативные функции записываются как уравнения. Соответственно их можно решать с помощью функции solve. Следующие примеры иллюстрируют задание уравнения окружности в общем и в частном (численном) виде:

Для графической визуализации импликативных функций служит функция implicitplot пакета plots. На рис. 7.2 представлено задание двух импликативных функций и построение их графиков.
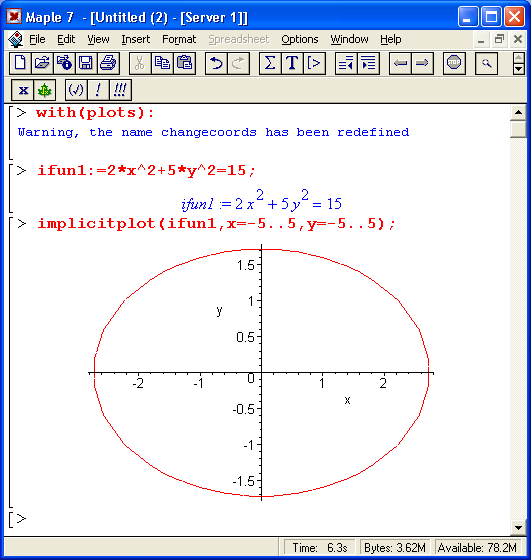
Рис. 7.2. Задание двух импликативных функций и построение их графиков
В данном случае задано построение двух эллипсов. Верхний — это окружность, сплюснутая по вертикали, а второй — наклонный эллипс.
Gif

Gif

Условные выражения
Условные выражения
Для подготовки разветвляющихся программ в Maple-язык программирования включен оператор if, позволяющий создавать следующую конструкцию:
if <Условие сравнения? then <Элементы>
|elif «Условие сравнения> then <Элементы>|
|e1se <Элементы>|
fi:
В вертикальных чертах | | указаны необязательные элементы данной конструкции. Следующих два вида условных выражений чаще всего используются на практике:
- if <Условие> then <Элементы 1> fi — если Условие выполняется, то исполняются Элементы 1, иначе ничего не выполняется;
- if <Условие> then <Элененты 1> else <Элененты 2> fi — если Условие выполняется, то исполняются Элементы 1, иначе исполняются Элементы 2.
В задании условий используются любые логические конструкции со знаками сравнения (<, <=, >, >=, =, <>) и логические операторы and, or и not, конструкции с которыми возвращают логические значения true и false. Рассмотрим следующий простой пример:
|
|
|
> х:-5:
> if x<0 then print('Negative') fi;
Negative
> x:-l: > if x<0 then print('Negative') fi;
В этом примере анализируется значение х. Если оно отрицательно, то с помощью функции вывода print на экран выводится сообщение «Negative». А вот если х неотрицательно, то не выводится никакого сообщения. В другом примере если х неотрицательно, то выводится сообщение «Positive»:
> х.— 5:
> if x<0 then print('Negative') else print('Positive') fi;
Negative > x:-l:
> if x<0 then printСNegative") else printC'Positive') fi;
Positive
Приведем еще один пример, показывающий особую форму задания конструкции if-then-else-fi:
> х:=-5:
> 'if (x<0, printCNegative').print('Positive'));
Negative
> х:=1:
> *1f (х<0. print("Negative'),printrPositive'));
Positive
В этой конструкции вида 'if '(Условие. Выражение1, Выражение2)
если Условие выполнятся, то будет исполнено Выражение!, в противном случае будет исполнено Выражение2. Ввиду компактности записи такая форма условного выражения нередко бывает предпочтительна, хотя она и менее наглядна. На рис. 7.3 представлено применение данной конструкции для моделирования трех типов сигналов.
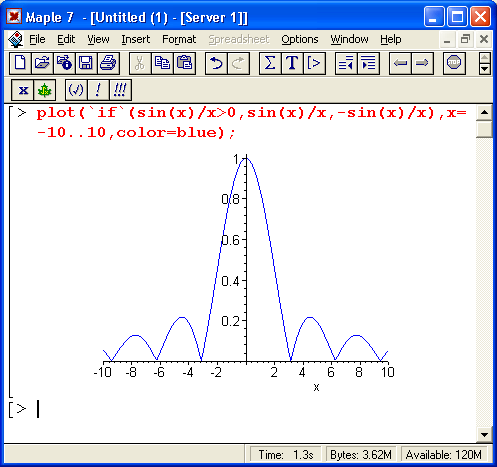
а
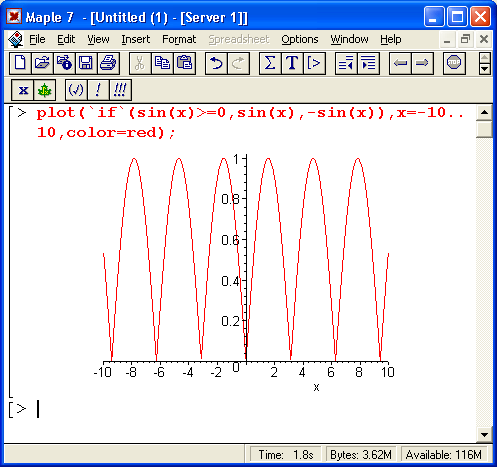
б

в
Рис. 7.3. Применение конструкции с функцией if для моделирования сигналов
К сожалению, функции на базе конструкции if не всегда корректно обрабатываются функциями символьной математики. Поэтому надо тщательно контролировать полученные в этом случае результаты.
Gif

Gif

Gif

Циклы for и while
Циклы for и while
Зачастую необходимо циклическое повторение выполнения выражения заданное число раз или до тех пор, пока выполняется определенное условие. Maple 7 имеет обобщенную конструкцию цикла, которая задается следующим образом:
| for <name>| |from <exprl>| |to <expr3>| |by <expr2>| (while <expr4>| do Statement sequence> od;
Здесь name — имя управляющей переменной цикла, exprl, ехрr2 и ехрrЗ — выражения, задающие начальное значение, конечное значение и шаг изменения переменной name, ехрr4 — выражение, задающее условие, пока цикл (набор объектов между словами do и od) будет выполняться.
|
|
|
В ходе выполнения цикла управляющая переменная меняется от значения exprl до значения ехрr2 с шагом, заданным ехрrЗ. Если блок by <ехрr2> отсутствует, то управляющая переменная будет меняться с шагом +1 при ехргКехрг2. Это наглядно поясняет следующий пример:
> for i front 1 to 5 do printd) od;
В нем выводятся значения переменной i в ходе выполнения цикла. Нетрудно заметить, что она и впрямь меняется от значения 1 до значения 5 с шагом +1. Следующий пример показывает, что границы изменения управляющей переменной можно задать арифметическими выражениями:
> for i from 7/(2+5) to 2+3 do printd) od:
А еще один пример показывает задание цикла, у которого переменная цикла меняется от значения 1 до 10 с шагом 2:
> for i from 1 to 10 by 2 do printd) od: 1 3 5 7 9
8 этом случае выводятся нечетные числа от 1 до 9. Шаг может быть и отрицательным:
> for i from 9 to 1 by -2 do print(i) od:
Следует отметить, что если exprl>expr2 задать заведомо невыполнимое условие, например, ехрr1>ехрг2 и положительное значение шага, то цикл выполняться не будет. Цикл можно прервать с помощью дополнительного блока while <ехрr4>. Цикл с таким блоком выполняется до конца или до тех пор, пока условие ехрг4 истинно.
> for i from 1 to 10 by 2 while i<6 do print(i) od:
Таким образом, конструкция цикла в Maple-языке программирования вобрала в себя основные конструкции циклов for и while. Есть еще одна, более специфическая конструкция цикла:
|for <name>| |in <exprl>| |whi1e <expr2>| do statement sequence> od:
Здесь exprl задает список значений, которые будет принимать управляющая переменная name. Цикл будет выполняться, пока не будет исчерпан список и пока выполняется условие, заданное выражением ехрг2. Следующий пример иллюстрирует сказанное:
> for i in [1.2,5,-1.7.12] do print(i) od;
2 5 -1 7
12 > for i in [1,2.5.-1,7.12] while i>0 do print(i) od:
2 5
В цикле этого вида управляющая переменная может меняться произвольно. Циклы могут быть вложенными. Это иллюстрирует следующий пример, создающий единичную матрицу на базе заданного массива М:
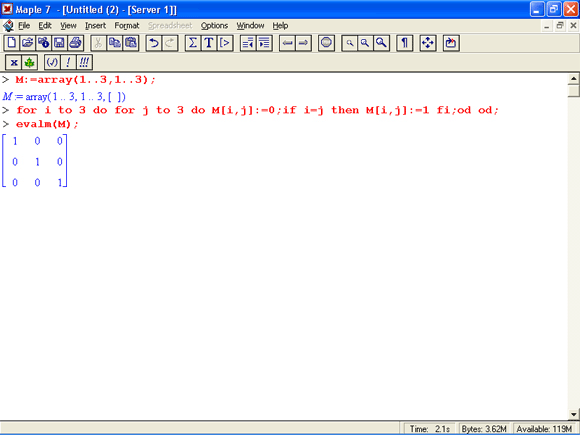
Этот пример имеет не более чем познавательное значение, поскольку для создания такой матрицы Maple 7 имеет функцию identity, с помощью которой функция array позволяет сразу создать единичную матрицу:
|
|
|
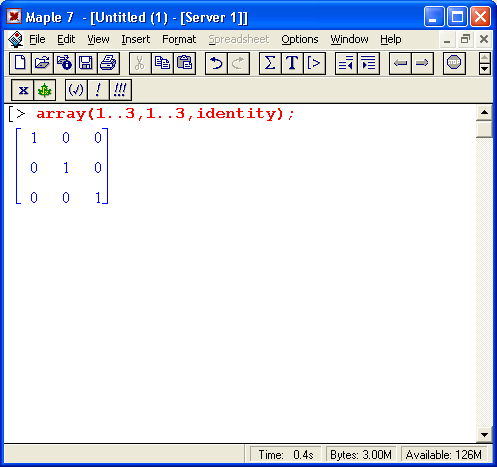
В заключение отметим, что возможна упрощенная частная конструкция цикла типа while:
while expr do statseq od:
Здесь выражения statseq выполняются, пока выполняется логическое условие ехрr. Пример такого цикла:
> n:=1:
n:=1.
> while n<16 do n:»2*n od;
n:=2
n:= 4
n:= 8
n:=16
В этом примере идет удвоение числа n с начальным значением n = 1 до тех пор, пока значение n меньше 16.
Gif

Gif

|
|
|


