 |
Доступная (метод снежного кома) выборка
|
|
|
|
Курзаева Любовь Викторовна
Анализ данных
Конспект лекций
Магнитогорск
Составитель: Л.В. Курзаева
Анализ данных - Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016. - 50 с.
Рецензент Г.Н.Чусавитина
© Курзаева Л.В., 2016

ОГЛАВЛЕНИЕ
Выборочный метод………………………………………………………….4
Построение и анализ одномерного распределения……………………14
Вычисление характеристик рядов распределения……………………18
Построение и анализ таблиц двухмерного распределения…………..28
Методы многомерного анализа данных………………………………..41
Введение в интеллектуальный анализ данных (Data Mining)……...48
Список литературы……………………………………………………….53
Выборочный метод
Одной из задач, которая стоит перед началом исследования, является сбор необходимых эмпирических данных об изучаемом явлении (процесса).
Множество элементов, составляющих объект исследования называют генеральной совокупностью. Важно, что генеральная совокупность - суммарная численность изучаемых объектов (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и времени.
Проведение исследования на основе изучения генеральной совокупности в целом ряде случаев является невозможным, либо нецелесообразным с учетом имеющегося ресурсного обеспечения исследования.
В этом случае применяется выборочное обследование. Суть выборочного метода заключена в том, что обследованию подвергается только часть элементов генеральной совокупности, которая называется выборочной совокупностью (часть объектов генеральной совокупности, выступающих в качестве объектов наблюдения).
|
|
|
Следует различать единицы отбора и единицы наблюдения. Единицами отбора являются единицы или группы единиц генеральной совокупности отбираемые на каждом этапе формирования выборки. Единицы наблюдения – это отобранные единицы генеральной совокупности, характеристики которых непосредственно измеряются. Если выборка проходит в несколько этапов (многоступенчатая выборка), то единицы отбора и единицы наблюдения могут не совпадать.
Однако для характеристики всей генеральной совокупности могут служить лишь репрезентативные (представительные) выборки, т.е. выборки, которые правильно отражают свойства генеральной совокупности.
В США одним из наиболее известных исторических примеров нерепрезентативной выборки считается случай, происшедший во время президентских выборов в 1936 году[1]. Журнал «Литрери Дайджест», успешно прогнозировавший события нескольких предшествующих выборов, ошибся в своих предсказаниях, разослав десять миллионов пробных бюллетеней своим подписчикам, а также людям, выбранным по телефонным книгам всей страны и людям из регистрационных списков автомобилей. В 25 % вернувшихся бюллетеней (почти 2,5 миллиона) голоса были распределены следующим образом:
· 57 % отдавали предпочтение кандидату-республиканцу Альфу Лэндону
· 40 % выбрали действующего в то время президента-демократа Франклина Рузвельта
На действительных же выборах, как известно, победил Рузвельт, набрав более 60 % голосов. Ошибка «Литрери Дайджест» заключалась в следующем: желая увеличить репрезентативность выборки, — так как им было известно, что большинство их подписчиков считают себя республиканцами, — они расширили выборку за счёт людей, выбранных из телефонных книг и регистрационных списков. Однако они не учли современных им реалий и в действительности набрали ещё больше республиканцев: во время Великой депрессии обладать телефонами и автомобилями могли себе позволить в основном представители среднего и высшего класса (то есть большинство республиканцев, а не демократов).
|
|
|
Из этого можно сделать один важный вывод - выборка имеет качественные и количественные характеристики
Качественная характеристика выборки – кого именно мы выбираем и как способы построения выборки мы для этого используем.
Количественная характеристика выборки – сколько человек выбираем, другими словами объём выборки.
Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от ошибки никак не зависит от размера выборки.
В статистике доказано: чтобы выборка была репрезентативной, она должна быть случайной, т.е. каждая единица генеральной совокупности должна иметь равный шанс попасть в выборку.
Рассмотрим случайные и неслучайные виды выборок.
Неслучайные выборки:
Доступная (метод снежного кома) выборка
Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)
Стихийная выборка
Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов.
Направленная (целевая) выборка. Формирование состава участников эксперимента (например, формирование контрольных групп точечным методом, когда для каждого участника основной группы подбирается участник контрольной группы, обладающий сходными признаками). Это один из тех редких случаев, когда нет необходимости в проведении случайного отбора.
|
|
|
Отбор экспертов, который может проводиться на основе следующих критериев:
• объективные характеристики экспертов, содержащиеся в документах
• тестирование кандидатов в эксперты
• взаимный отбор
• самооценка кандидатов в эксперты.
Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает проблема выбора признака и определения его типичного значения.
Квотная выборка
Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно.
Развитие теории вероятностей позволило теоретически обосновать возможность применения выборочного метода. В основе теоретического обоснования выборочного метода лежит так называемый закон больших чисел. Физический смысл этого закона можно выразить следующим образом:
«при очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности»
Таким образом, задачей исследователя, в распоряжении которого имеются сплошные данные, является организация выборочного изучения этих данных путем формирования репрезентативной выборки. Если же он имеет дело с данными ранее проведенных выборочных обследований, необходимо проверить, как были организованы эти обследования, не нарушались ли принципы случайного отбора.
Существует несколько видов выборочного изучения, позволяющих формировать репрезентативные выборки: случайный, механический, типический и серийный отбор.
|
|
|
Случайным (собственно случайным, простым случайным) является такой отбор, при котором все элементы генеральной совокупности имеют равную возможность быть отобранными. На практике случайный отбор производится с помощью жеребьевки или использования разработанных в статистике таблиц случайных чисел. При жеребьевке может осуществляться бесповторный отбор (когда выбранный элемент больше не участвует в выборке) или повторный (когда ему предоставляется шанс еще раз быть выбранным). При большом объеме генеральной совокупности проведение жеребьевки или использование таблиц случайных чисел становятся затруднительными, тогда применяют другие виды выборочного изучения.
Механическая (систематическая) выборка - отбор сводится к тому, что генеральная совокупность разбивается на равные части и из каждой части берется одна единица. Например, 7, 17, 27, 37 и т.д.
Однако механическим отбором следует пользоваться очень осторожно, поскольку элементы исходной совокупности могут быть упорядочены, что может привести к возникновению систематических ошибок. Необходимо проанализировать изучаемую совокупность и применять механический отбор лишь в том случае, если элементы генеральной совокупности расположены случайным образом.
Механический отбор достаточно широко использовался в русской статистике. Например, механический отбор применялся земскими статистиками для обследований части крестьянских хозяйств не по обычной подворной карточке, а по особой расширенной программе. С помощью механического отбора изучалось состояние 25 млн. крестьянских хозяйств и накануне сплошной коллективизации, когда они были подвергнуты 10%-ному весеннему опросу и 5%-ному осеннему опросу.
Типическая (стратифицированная) выборка - отбор заключается в том, что генеральная совокупность разбивается на типические группы, образованные по какому-либо признаку. Затем из каждой выделенной группы отбираются единицы либо случайно, либо механически. Например, территория, подлежащая обследованию, разделяется на районы, отличающиеся социально-экономическими или географическими условиями, и из каждого района производят отбор единиц в выборку. При этом допускается как отбор, пропорциональный численности отдельных типических групп, так и непропорциональный. Понятно, что более предпочтительным является пропорциональный отбор, поскольку он дает более точные результаты.
Серийная (гнездовая или кластерная)выборка - отбор предусматривает разбиение всей генеральной совокупности на группы (серии), из которых путем случайного или механического отбора выделяется их определенная часть, которая и подвергается сплошной обработке. Фактически, серийный отбор представляет собой случайный или механический отбор, произведенный для укрупненных элементов исходной совокупности. Например, обследуются не единичные крестьянские хозяйства, а целые деревни или имения.
|
|
|
Итак, выборочный метод позволяет экстраполировать результаты обследования выборки на всю генеральную совокупность. При этом надо иметь в виду, что всегда будет возникать некоторая ошибка, показывающая, насколько хорошо характеристики выборки отражают соответствующие характеристики генеральной совокупности.
Ошибки, возникающие при использовании выборочных данных для суждения обо всей генеральной совокупности, называются ошибками выборки (репрезентативност)и. Они бывают систематическими и случайными.
Систематические ошибки – ошибки, возникающие при использовании выборочных данных, если не выполняются условия случайного отбора. Случайные ошибки – ошибки, возникающие при использовании выборочных данных за счет того, что для анализа всей совокупности используется только ее часть. Величина ошибки выборки – это разность между генеральной и выборочной средними.
Введем следующие обозначения основных характеристик генеральной и выборочной совокупности(табл.1)
Таблица 1
Обозначение генеральных и выборочных характеристик
| Показатель | генеральная совокупность | выборочная совокупность |
| Объем | N | n |
| Численность единиц, обладающих исследуемым значением признака | М | m |
| Средний размер признака | 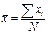
| 
|
| Доля единиц, обладающих исследуемым значением признака | р= M / N | ω= m / n |
| Доля единиц, обладающих остальными значениями признака | q= 1 –p | ( 1 –ω) |
| Дисперсия признака | 
| 
|
| Дисперсия доли |  = p( 1 –p) = p( 1 –p)
|  = ω( 1 –ω) = ω( 1 –ω)
|
В математической статистике существуют формулы для вычисления средней ошибки выборки на основе данных той выборки, с которой работает исследователь (табл.2). Для различных видов выборочного изучения средняя ошибка выборки определяется по-разному.
Таблица 2
Средняя ошибка выборки
| Для количественных признаков (ошибка средней) | Для атрибутивных признаков (ошибка доли) | |
| Повторный отбор |  
| 
|
| Бесповторный отбор |  
| 
|
Для бесповторного отбора ошибка определяется по формулам, учитывающим величину  . В тех случаях, когда генеральная совокупность очень велика по сравнению с выборочной, эта величина близка к единице, поэтому ею можно пренебречь. Тогда ошибку выборки при бесповторном отборе рассчитывают по формулам для повторного отбора.
. В тех случаях, когда генеральная совокупность очень велика по сравнению с выборочной, эта величина близка к единице, поэтому ею можно пренебречь. Тогда ошибку выборки при бесповторном отборе рассчитывают по формулам для повторного отбора.
При расчете ошибок малой выборки формула средней ошибки имеет вид:  .
.
Средняя ошибка выборки позволяет по выборочной средней судить о значении генеральной средней. Однако в конкретном выборочном исследовании ошибка может существенно отличаться от средней ошибки, превышая ее. Поэтому более эффективным является определение тех границ, в которых «практически наверняка» находится действительная ошибка, допущенная в данной конкретной выборке.
Теорема Чебышева–Ляпунова: При достаточно большом количестве наблюдений и при ограниченной дисперсии можно утверждать, что вероятность того, что разница показателей генеральной и выборочной совокупности не превышает заданного предела tμ, стремится к единице. Таким образом, предельная ошибка выборки: Δ=tμ.
Вероятность данного события называют доверительной вероятностью. Величину t называют коэффициентом доверия. Он зависит от уровня доверительной вероятности (табл.3)
Таблица 3
Краткая таблица значений t-критерия
| t | 1,00 | 1,96 | 2,00 | 2,58 | 3,00 |
| Φ(t) | 0,683 | 0,950 | 0,954 | 0,990 | 0,997 |
То есть, с вероятностью 0,954 можно утверждать, что ошибка выборки не превысит удвоенной средней ошибки выборки, с вероятностью 0,997 можно утверждать, что ошибка выборки не превысит утроенной средней ошибки выборки.
Для малой выборки предельная ошибка выборки вычисляется по формуле:
 ,
,
где t рассчитывается исходя из так называемого закона распределения Стьюдента с k степенями свободы (в отличие от больших выборок, где t вычисляется на основе нормального закона распределения),  .
.
Связь между коэффициентом t и вероятностью P в распределении Стьюдента сложнее, чем в нормальном распределении и определяется с учетом объема выборки.
В статистических исследованиях с помощью формулы предельной ошибки можно решать ряд задач.
1. Определять возможные пределы нахождения характеристики генеральной совокупности на основе данных выборки. Доверительные интервалы для генеральной средней можно установить на основе соотношения  .
.
Доверительные интервалы для генеральной доли устанавливаются на основе соотношения  .
.
С этими величинами тесно связаны следующие характеристики измерения: точность и надежность. Надежность отражена в доверительной вероятности: чем больше доверительная вероятность, тем выше надежность измерения. Точность оценок отражена в доверительном интервале – пределах, в которых с заданной степенью вероятности заключена неизвестная величина оцениваемого параметра. Характеристики выборочной совокупности мы выявляем в результате исследования, характеристики генеральной совокупности можем оценить при помощи доверительного интервала: то есть, чем больше предельная ошибка, тем выше надежность, но тем ниже точность оценивания характеристик генеральной совокупности. Поэтому зачастую довольствуются несколько меньшей доверительной вероятностью. В социологических исследованиях обычно допустимой считается предельная ошибка доли 0,05.
Пример. Пусть была произведена выборка 1600 человек. Средний возраст по выборке – 30 лет, среднеквадратическое отклонение – 10 лет. Необходимо найти доверительный интервал.
Прежде всего, необходимо задать надежность оценки. Возьмем 95% надежность. Поскольку выборка большая, воспользуемся таблицей значений функции Лапласа и найдем коэффициент доверия t=1,96.
Тогда
 .
.
С вероятностью 95% истинное средний возраст по ГС находится в интервале от 29,51 лет до 30,49 лет.
Пример. Из 200 опрошенных 55% - женщины. Действуем аналогично примеру 1. Выборку также можно считать большой. Тогда  =1,96 для 95% надежности.
=1,96 для 95% надежности.
 .
.
С вероятностью 95% доля женщин в ГС находится в интервале от 48% до 62%.
Пример. По урожайности зерновых культур 10 агрофирм определить среднюю и предельную ошибки выборки и оценить пределы для генеральной средней.
Исходные данные (xi, i = 1,…10 - урожайность зерновых в центнерах с гектара) и промежуточные вычисления можно записать в табл.4
Таблица 4
Расчетная таблица
| № | 
| 
| 
|
| 6,5 | -0,2 | 0,04 | |
| 6,2 | -0,5 | 0,25 | |
| 5,4 | -1,3 | 1,69 | |
| 9,3 | 2,6 | 6,76 | |
| 7,2 | 0,5 | 0,25 | |
| 8,4 | 1,7 | 2,89 | |
| 4,3 | -2,4 | 5,76 | |
| 6,0 | -0,7 | 0,49 | |
| 6,3 | -0,4 | 0,16 | |
| 7,4 | 0,7 | 0,49 |
Получим:




Для P=0,95 t=2,26 Þ D=t  »1,04 Þ
»1,04 Þ 
Очевидно, что полученная предельная ошибка (15%) слишком велика и объем выборки в 10 единиц не достаточен для суждения о реальной средней урожайности зерновых.
2. Определять необходимый объем выборки с помощью допустимой величины ошибки
Средняя ошибка выборки связана с объемом выборки и степенью разброса значений признака в генеральной совокупности. Увеличение дисперсии увеличивает ошибку выборки, увеличение объема выборки уменьшает ошибку выборки. Из формулы предельной ошибки можно рассчитать объем выборки (табл. 5)
Таблица 5
Формулы расчета объема выборок
| Для количественных признаков (ошибка средней) | Для атрибутивных признаков (ошибка доли) | |
| Повторный отбор | 
| 
|
| Бесповторный отбор | 
| 
|
Доверительная вероятность задается исследователем. Сложность заключается в том, что для расчета объема выборки необходимо знать дисперсию признака, который должен бить измерен в ходе исследования. Эта проблема решается следующими способами:
1. Можно провести пробное обследование, на базе которого определяется величина дисперсии признака, используемая в качестве оценки генеральной дисперсии.
2. Можно использовать данные прошлых обследований, проводившихся в аналогичных целях, то есть дисперсия, полученная по их результатам, используется в качестве оценки генеральной дисперсии.
3. Если нас интересует не среднее значение признака, а доля единиц, обладающих данным значением в совокупности, можно использовать максимально возможную дисперсию, равную 0,25.
Определяя численность выборки и ее точность, следует учитывать, что чем больше абсолютный объем выборки, тем менее ощутимо влияет на точность результата включение в выборку дополнительных десятков и даже сотен единиц и тем больших затрат требует дальнейшее увеличение точности. Кроме того, объем выборки зависит от предполагаемой группировки объектов, т.е. чем больше будет групп, тем больше должна быть выборка.
Пример. Для рассмотренных в примере 3 данных об урожайности зерновых культур в колхозах определим требуемый объем выборки.
Зададим предельную ошибку выборки, равную 5%, она будет равна D=0,34, тогда, подставляя в формулу  значения t=2,26; s=1,37 и D, получим n=86. Таким образом, для определения средней урожайности зерновых в колхозах с вероятностью 95% и точностью 5% необходимо произвести выборку, объемом 86 единиц.
значения t=2,26; s=1,37 и D, получим n=86. Таким образом, для определения средней урожайности зерновых в колхозах с вероятностью 95% и точностью 5% необходимо произвести выборку, объемом 86 единиц.
Построение и Анализ одномерного распределения
Одномерное распределение – это результат группировки единиц совокупности на основе одной переменной. Построение и дальнейший анализ одномерного распределения основывается на представлении данных в виде ряда распределения, который является исходным для применения методов описательной статистики.
Ряды распределения могут быть: атрибутивными, то есть построенными по признаку, т.е. измеренному в шкале качественного типа – номинальной или порядковой, и вариационными, то есть построенными по количественному признаку.
В зависимости от вида вариации ряд может быть дискретным или интервальным.
Дискретный вариационный ряд – это ряд, значения вариант которого выражены одним числом (значением признака).
Интервальный вариационный ряд это ряд, варианты которого выражены двумя числами (значениями признака), являющимися нижней и верхней границами интервала. Такие ряды обычно используются в случаях, когда число вариантов дискретного признака слишком велико, а также когда анализу подлежат вариации непрерывного признака. Интервалы в ряду могут быть как равными, так и неравными. Это зависит от характера статистических данных и задач исследования.
Вариационный ряд может быть асимметричным, т.е. таким, в котором наибольшей частотой обладают крайние значения вариант.
Частота – это величина, равная числу встречаемости признака в совокупности. Сумма частот равна количеству единиц наблюдения.
В социологии используются следующие разновидности частот:
Число опрошенных – сколько всего человек приняло участие в опросе, т.е. число ответивших и число не ответивших.
Число ответивших – сколько человек ответило на данный вопрос.
Число ответов – сколько ответов было дано на данный вопрос.
Число не ответивших – сколько человек не ответило на данный вопрос.
Частоты представляют собой абсолютный показатель распределения, а относительным показателем является частость (доля). Частость представляет собой отношение частоты встречаемости данного признака к сумме всех частот. Ее можно выражать как непосредственно в долях (тогда сумма частостей ряда будет равна единице), так и в процентах (тогда сумма частостей ряда будет равна 100%).
В социологии используются следующие виды процентов:
% от числа ответивших: единицей анализа в данном случае является человек, ответивший на данный вопрос, то есть не ответившие будут игнорироваться. За 100 % берется число ответивших.
% от числа опрошенных: рассчитывается для того, чтобы определить долю ответивших и не ответивших на данный вопрос. За 100% берется число опрошенных.
% от числа данных ответов: единицей анализа в данном случае выступает не человек, а его ответ. Здесь за 100 % выступает общее число данных ответов.
Примером дискретного ряда может служить распределение студентов по курсам:
| Курс | Количество студентов, чел. |
| 1-й | |
| 2-й | |
| 3-й | |
| 4-й | |
| 5-й | |
Графически эти данные можно отобразить в виде гистограммы (рис. 1).

Рис. 1. Гистограмма распределения количества студентов
по курсам (дискретный вариационный ряд)
Визуальный анализ гистограмм позволяет выявить характер распределения данных и ответить на следующие шесть вопросов:
1. Какие значения типичны для заданного набора данных?
2. Как различаются между собой значения (диапазон значений)?
3. Сконцентрированы ли данные вокруг некоторого типичного значения?
4. Какой характер имеет эта концентрация данных? В частности, одинаков ли характер «затухания» для малых и больших значений данных?
5. Есть ли в заданном наборе такие значения, которые сильно отличаются от остальных и требуют специальной обработки (выбросы, т.е. такие значения, которые либо слишком велики, либо слишком малы.)?
6. Можно ли сказать, что в целом это однородный набор или отчетливо наблюдается наличие групп, которые надо анализировать отдельно?
Интервальный ряд распределения – это ряд, в котором значения признака заданы в виде интервала. Например, распределение студентов по младшим и старшим курсам можно представить в виде интервального ряда:
| Курс | Количество студентов, чел. |
| 1–2-й | |
| 3–5-й | |
При этом графическое представление интервального ряда в виде гистограммы представлено на рис. 2.

Рис. 2. Гистограмма распределения количества студентов
по курсам (интервальный вариационный ряд)
При определении интервальных рядов распределения необходимо определить, какое число групп следует образовать и какие взять интервалы (равные, неравные, закрытые, открытые).
При установлении количества интервалов можно воспользоваться следующей формулой: r» [1+3,2 lg(n)], (r – количество интервалов, n – количество данных). Для того чтобы вариационный ряд не был слишком громоздким, обычно число интервалов берут от 6 до 11.
Вычисление характеристик рядов распределения
Описательная статистикаохватывает методы описания статистических данных, представления их в форме рядов распределений.
Условно все характеристики рядов распределения можно разделить на четыре группы:
1. Показатели, характеризующие закон распределения.
2. Показатели, характеризующие центральную тенденцию (меры среднего уровня).
3. Показатели (меры), характеризующие рассеяние относительно центральной тенденции.
4. Показатели асимметрии.
Рассмотрим их подробнее.
Показатели, характеризующие закон распределения. Это, прежде всего, уже знакомые нам частоты и проценты, а также накопленные частоты и проценты.
Как для абсолютных, так и для относительных частот можно определить кумулятивные показатели – накопленные частоты и проценты, которые рассчитывается путем суммирования всех частот (процентов) до выбранной категории включительно.
Упомянем также квартили, разбивающие ранжированный ряд значений признака на 4 части по 25% значений в каждой. Квартили при этом называются нижней, средней и верхней (при этом, очевидно, средняя квартиль совпадает с медианой). Аналогично можно ввести децили, разбивающие вариационный ряд значений на группы по 10% чисел и другие квантили – числа, разбивающие упорядоченную совокупность значений признака на равные по объему части.
Показатели, характеризующие центральную тенденцию (меры среднего уровня). Среднее арифметическое представляет собой количественную характеристику качественно однородной совокупности. Наиболее распространенными средними являются средняя арифметическая, мода и медиана.
Среднее арифметическое ( ) – обобщающий показатель, выражающий типичные размеры количественных признаков качественно однородных явлений, определяется по формуле:
) – обобщающий показатель, выражающий типичные размеры количественных признаков качественно однородных явлений, определяется по формуле:
 ,
,
где xi – варианта с порядковым номером  (
( =1,…n); n – объем совокупности.
=1,…n); n – объем совокупности.
Для интервального ряда используется средняя арифметическая взвешенная:
 ,
,
где fi – частота индивидуального значения признака;
k – количество градаций признака.
Мода ( ) – варианта, которая чаще всего встречается в данном упорядоченном ряду. Если таких вариант несколько, то берется первая из них в упорядоченном ряду.
) – варианта, которая чаще всего встречается в данном упорядоченном ряду. Если таких вариант несколько, то берется первая из них в упорядоченном ряду.
Пример. Ряд: 4,5,5,6,6,7. В данном ряду мода число 5.
В интервальном ряду по определению можно установить только модальный интервал, при этом значение моды определяется по формуле:
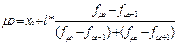 ,
,
где x0 – нижняя граница модального интервала;
l – величина интервала;
f μo – частота модального интервала;
f μo–1 – частота предмодального интервала;
f μo+1 – частота послемодального интервала.
Медиана ( ) – варианта, находящаяся в середине упорядоченного ряда:
) – варианта, находящаяся в середине упорядоченного ряда:
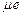 =
=  , если число вариант нечетно (n=2m+1);
, если число вариант нечетно (n=2m+1);
 =
=  , если число вариант четно (n=2m).
, если число вариант четно (n=2m).
Пример. Ряд: 4,5,5,6,6,7. Медиана равна 5,5 (ряд четный).
Ряд:4,5,5,6,6,7,8. Медиана равна 6 (ряд нечетный).
Медиана используется, когда изучаемая совокупность неоднородна. Особое значение она приобретает при анализе асимметричных рядов – она дает более верное представление о среднем значении признака, т.к. не столь чувствительна к крайним (нетипичным в плане постановки задачи) значениям, как средняя арифметическая.
Для интервального ряда можно определить как медианный интервал, а сама медиана рассчитывается по формуле:
 ,
,
где x0 – нижняя граница медианного интервала;
l – величина интервала;
n – количество единиц в совокупности;
s μe–1 – накопленная частота предмедианного интервала;
f μe – частота медианного интервала.
Пример. Выборка результатов контрольного тестирования дала следующий интервальный ряд (табл.6)
Таблица 6
Интервальный ряд по результатам тестирования
| Интервалы баллов | До 70 | 70–80% | 80–90% | 90-100% |
| Частота |
Определим среднее арифметическое и моду, медиану по выборке.
1. Рассчитаем выборочную среднюю

 (см. расчетную табл. 7)
(см. расчетную табл. 7)
Таблица 7
Расчетная таблица
| xi | fi | xi' (середины интервалов) | xi'*fi |
| 60-70 | |||
| 70-80 | |||
| 80-90 | |||
| 90-100 | |||
| Итого Σ |
2. Вычислим моду. Для этого сначала определим модальный интервал (интервал с наибольшей частотой). В нашем примере это интервал 80-90% с частотой равной 40.
Исходя из этого легко определить необходимые величины:
x0 =80;
l = 10;
f μo = 40;
f μo–1 =25;
f μo+1 =20.
Подставляем в формулу найденные значения для расчета моды интервального ряда:
 .
.
2. Вычислим медиану. Для определения медианного интервала необходимо создать ряд накопленных частот (табл. 8):
Таблица 8
Расчетная таблица
| Интервалы баллов | До 70 | 70–80% | 80–90% | 90-100% |
| Частота | ||||
| Накопленные частоты | 10+25=35 | 35+40=75 | 75+20=95 |
Чтобы найти медианный интервал нужно объем выборки увеличенный на единицу разделить на 2 (т.е.(n+1)/2), а затем найти первый интервал, накопленная частота которого превышает либо равна полученному значению. В нашем случае (n+1)/2=48, а судя по ряду накопленных частот медианным является интервал 80-90%.
Находим:
x0 = 80;
l =10;
n = 95;
s μe–1 = 35;
f μe =40.
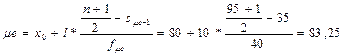 ,
,
Показатели (меры), характеризующие рассеяние относительно центральной тенденции. Средние позволяют охарактеризовать статистическую совокупность одним числом, однако, не содержат информации о том, насколько хорошо они представляют эту совокупность. Для определения того, насколько сильно варьируются значения признака, используются такие характеристики, как размах вариации, дисперсия и среднее квадратическое отклонение.
Все они показывают, насколько сильно варьируют значения признака (а точнее – их отклонения от среднего) в данной совокупности. Чем меньше значение меры разброса, тем ближе значения признака у всех объектов к своему среднему значению, а значит, и друг к другу. Если величина меры разброса равна нулю, значения признака у всех объектов одинаковы.
Размах вариации (R) – это разность между наибольшим и наименьшим значениями признака:
 ,
,
где xmax – максимальное значение признака;
xmin – минимальное значение признака.
Показатель этот достаточно просто рассчитывается, однако является наиболее грубым из всех мер рассеяния, поскольку при его определении используются лишь крайние значения признака, а все другие просто не учитываются.
При расчете двух других характеристик меры вариации признака испо
|
|
|


