 |
Оценка силы и направления связи
|
|
|
|
Оценить силу связи можно при помощи величины коэффициента корреляции по модулю. Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0,1 до 0,3; умеренная — от 0,3 до 0,5; заметная — от 0,5 до 0,7; высокая — от 0,7 до 0,9; весьма высокая (сильная) — от 0,9 до 1,0.
Направление связи оценивается с помощью знака коэффициента корреляции. Положительный коэффициент говорит о наличии прямой связи, а отрицательный – о наличии обратной связи.
Выбор коэффициента корреляции зависит от уровня, на котором замерены данные. Как мы помним, для шкал более высокого уровня можно использовать все показатели, которые используются для шкал более низкого уровня, но не наоборот. Для оценки связи между номинальными переменными, можно использовать только коэффициенты, основанные на совместном появлении событий.
Коэффициент Крамера, основан на использовании критерия χ2:
 ,
,
где n – общее число ответивших на оба вопроса,
m – число строк,
k – число столбцов,
min – надо выбрать наименьшее
Коэффициент Крамера измеряется от 0 до 1, причем, чем ближе коэффициент к 1, тем сильнее связь между двумя переменными. Коэффициент Крамера имеет смысл использовать только в том случае, если связь при помощи χ2 признана значимой.
Если мы оцениваем связь двух дихотомических признаков, то мы можем использовать некоторые специфические меры связи. Для таких признаков строится корреляционная таблица размером 2*2, которая имеет следующий вид (табл.13)
Таблица 13
Корреляционная таблица
| B | 
| Σ | |
| A | a | b | a+b |

| c | d | c+d |
| Σ | a+c | b+d | n |
Для нее рассчитываются следующие коэффициенты:
| Коэффициент ассоциации Юла | Коэффициент контингенции | |

| 
|
Эти коэффициенты обладают следующими свойствами:
|
|
|
1. Изменяются в интервале (–1;+1), обращаются в 0 в случае отсутствия связи.
2. Q отражает полную связь (все А=В, но не все В=А), а Φ – абсолютную (все А=В, и все В=А).
3. Q обращается в 1(–1), если хотя бы в одной клетке таблицы частота равна 0, а Φ обращается в 1(–1), если 0 в двух клетках.
Для метрических и порядковых признаков могут использоваться меры, основанные на принципе ковариации, то есть на изучении совместных изменений в значениях признаков.
Коэффициент Пирсона можно использовать только для метрических шкал. Он имеет формулу:

где X – значение независимой переменной,
Y – значение зависимой переменной,
N – объем совокупности.
Обе переменные X и Y должны быть в дискретном виде.
Значимость коэффициента можно оценить следующим образом.
Для случая, когда объем совокупности меньше 50, рассчитывается t-критерий по формуле 
Для случая, когда объем совокупности больше 50, рассчитывается Z-критерий по формуле 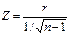
В большинстве случаев востребованным и весьма полезным может оказаться построение и анализ диаграмм рассеяния. Диаграмма рассеяния (точечная диаграмма) – математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости. На такой диаграмме производится визуальный анализ объектов исследования с учетом по форме связи («облака» точек) и по наличию выбросов на диаграмме рассеяния. «Выбросы» – крайние значения признаков, не характерные для данной выборки, слишком большие или слишком малые значении, аномальные, при удалении которых связь полностью может измениться.
Коэффициент ранговой корреляции Спирмена позволяет определить силу и направление связи между двумя признаками или двумя иерархиями признаков:
 ,
,
где di – разница между парой рангов,
l – количество сравниваемых пар рангов
|
|
|
Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы.
В случае 1, когда сравниваются два признака, ранжируются индивидуальные значения по первому признаку, полученные испытуемыми, а затем индивидуальные значения по другому признаку. Если два признака связаны положительно, то испытуемые, имеющие низкие ранги по одному из них, будут иметь низкие ранги и по другому, а испытуемые, имеющие высокие ранги по одному из признаков, будут иметь по другому признаку также высокие ранги. Если же корреляция отсутствует, то все ранги будут перемешаны и между ними не будет никакого соответствия. В случае отрицательной корреляции низким рангам испытуемых по одному признаку будут соответствовать высокие ранги по другому и наоборот.
В случае 2, когда сравниваются две иерархии признаков, ранжируются значения, полученные в двух группах по определенному, одинаковому для двух групп набору признаков. Если эти иерархии связаны положительно, то признаки, имеющие низкие ранги в одной группе, будут иметь низкие ранги и в другой группе и наоборот. При отрицательной корреляции картина обратная: признаки, имеющие высокие ранги в одной группе, имеют низкие ранги в другой.
Значимость коэффициента Спирмена определяется при помощи таблицы критических значений (см. Приложение).
В социологических исследованиях часто объект удается охарактеризовать не по абсолютной, а по относительной интенсивности свойства. Таким образом, известна лишь последовательность, в которой располагаются объекты, то есть каждый объект описывается с помощью рангов по каждому признаку. Еще один коэффициент ранговой корреляции – коэффициент Кендалла – строится на основе отношений типа «больше – меньше» и имеет формулу:
 ;
;
где l – количество сравниваемых пар рангов
S – расчетная величина
S можно рассчитать следующим образом. Для расчета числа согласованных и несогласованных рангов упорядочивают ранжированные ряды по одному из признаков. После этого, рассматривая ранги для другого признака, подсчитывается для каждого ранга количество рангов, больше данного, находящихся в таблице ниже него. Это будут значения S+, то есть число согласованных рангов. После этого, подсчитывают для каждого ранга количество рангов, меньше данного, находящихся в таблице ниже него. Это будут значения S–, то есть число несогласованных рангов. Затем из каждого количества согласованных рангов вычитают количество несогласованных рангов. Сумма этих величин и будет величина S.
|
|
|
Значимость коэффициента Кендалла определяется при помощи t-критерия Стьюдента, рассчитываемого по формуле:
 ,
,
где l – количество сравниваемых пар рангов;
S – расчетная величина.
Интерпретация коэффициента аналогична интерпретации коэффициента Спирмена.
Когда нам необходимо проанализировать изменение вариации значений одного признака под влиянием другого, имеет смысл использовать η-коэффициент (корреляционное отношение). Его использование основано на правиле сложения дисперсий.
Правило сложения дисперсий. Если рассчитать дисперсию признака по всей изучаемой совокупности, то она будет характеризовать вариацию как результат влияния всех факторов, определяющих индивидуальные различия в совокупности. Если же нужно выделить влияние какого-то одного фактора, то совокупность разбивают на группы, положив в основу группировки этот фактор. Выполнение такой группировки позволяет разбить общую дисперсию на две дисперсии, одна из которых будет характеризовать часть вариации, обусловленную влиянием интересующего нас фактора, а вторая – вариацию под воздействием всех прочих факторов.
Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия, которая является мерой колеблемости групповых средних вокруг общей средней:
 ,
,
где m – число групп
nj – число единиц в j-ой группе;
 – средняя арифметическая поj-ой группе;
– средняя арифметическая поj-ой группе;
 – общая средняя арифметическая.
– общая средняя арифметическая.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия:
 ,
,
где xij – индивидуальное значение признака;
 – средняя арифметическая поj-ой группе;
– средняя арифметическая поj-ой группе;
nj – количество единиц в совокупности.
|
|
|
По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий:
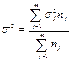 ,
,
где  – внутригрупповая дисперсия;
– внутригрупповая дисперсия;
nj – количество единиц в совокупности.
Между общей дисперсией, внутригрупповой дисперсией и средней из внутригрупповых дисперсий существует соотношение, определяемой правилом сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий: 
Для оценки влияния фактора нужно рассчитать долю межгрупповой дисперсии в общей – корреляционное отношение:
 ,
,
где ηmin=0, если δ2= 0, тогда фактор не играет роли;
ηmax=1, если δ2=σ20 (σ2l= 0 ), тогда вариация полностью обусловлена изучаемым фактором.
Проверить значимость η-коэффициента можно при помощи Z- критерия следующим образом:
 , где N – объем совокупности.
, где N – объем совокупности.
|
|
|


