 |
Распределение количества деревьев по ступеням толщины в сосняке брусничном
|
|
|
|
Распределение количества деревьев по ступеням толщины в сосняке брусничном
| Ступень толщины, см | Возраст, лет | |
| Всего | ||
В а р и а н т 1 0
Распределение количества деревьев по ступеням толщины в сосняке брусничном
| Ступень толщины, см | Возраст, лет | |
| Всего | ||
Рис. 3. Ряды распределения деревьев по ступеням толщины в 30, 40 и 50 лет
Определите и сравните между собой статистические показатели рядов распределения в начале и в конце периода наблюдений по форме табл. 46. Объясните изменение этих показателей.
Т а б л и ц а 4 6
Статистические показатели для____________________________________
| Показатели | Период наблюдений/ возраст, лет | |
| на начало опыта / 35 лет | на конец опыта / 75 лет | |
| Среднеарифметическая величина диаметра и ее ошибка, см | ||
| Среднеквадратическое отклонение, см | ||
| Коэффициент вариации, % | ||
| Точность исследования, % | ||
| Коэффициент асимметрии | ||
| Коэффициент эксцесса | ||
Расчет статистических показателей производится по формулам (30-37): М – среднее значение диаметра, см
М = 
, (30)
где f – количество деревьев в данной ступени толщины, экз.; W – середина ступени толщины, см (4, 8, 12, 16 и т. д. ); n – общее количество деревьев одного возраста, экз.
Одним средним значением нельзя отобразить все характерные черты статистической совокупности. Необходимо знать разброс (рассеивание) измеряемой величины относительно среднего значения. Основными показателями изменчивости являются выборочная дисперсия, среднеквадратическое отклонение и коэффициент вариации.
|
|
|
Среднеквадратическое отклонение выражается в тех же единицах измерения, что и среднеарифметическая величина, а коэффициент вариации – в процентах. Изменчивость ряда будет малой, если коэффициент вариации не превышает 10%; средней, если находится в пределах 11-30%, и большой, если находится за пределами 31%.
Результат исследования оценивается показателем точности наблюдений. Исследования достаточно точны, если он не превышает 5%; если находится в пределах 6-10%, то удовлетворительны. В некоторых случаях можно довольствоваться даже более 10%.
Для больших выборок вычисляют еще два показателя: косость (асимметрия) – А и крутость (эксцесс) – ε.
Если распределение скошено влево (в сторону тонких деревьев), то асимметрия отрицательная; если вправо (в сторону толстых деревьев), то положительная. Коэффициент асимметрии менее 0, 5 признается малым; от 0, 5 до 1, 0 – средним и выше 1, 0 – большим.
Показатель крутости свидетельствует об отклонении распределения от нормального распределения. Эксцесс положителен при островершинной кривой и отрицательный – при плосковершинной.
Как правило, «высокая», «островершинная» кривая распределения с «узким» основанием свидетельствует об однородности древостоя. При этом следует отметить, что чем однороднее древостой, тем сильнее конкуренция.
Усиленная конкуренция в насаждениях ведет к естественному отпаду отставших в росте деревьев, который является результатом дифференциации в древостое. Вследствие этого изменяется его структура, увеличивается число крупных деревьев и соответственно повышается устойчивость лесной экосистемы. В связи с этим изменяется и вид кривой распределения деревьев по ступеням толщины. Она становится более «плоской», а ее основание «расширяется» приблизительно в 1, 5 раза, тем самым конкурентная нагрузка более равномерно распределяется по всей структуре древостоя и конкуренция ослабляется.
|
|
|
С – центральное отклонение, см: С =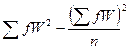 
. (31)
Среднеквадратическое отклонение (сигма), см: σ = 
. (32)
Ошибка средней, см: m = 
. (33)
CV – коэффициент вариации, %: CV = 
. (34)
Р – точность исследования, %: Р =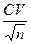 
. (35)
А – коэффициент асимметрии: А =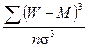 
. (36)
ε – коэффициент эксцесса: ε =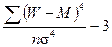 
. (37)
При расчетах используйте табл. 47.
Т а б л и ц а 4 7
|
|
|
