Расчет и конструирование базы колонны

Собственный вес колонны:

кг.

Расчетная нагрузка на базу колонны:

кН.

Требуемая площадь плиты базы колонны

,

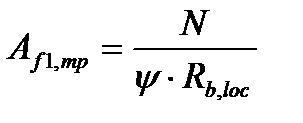где y - коэффициент, зависящий от характера распределения местной нагрузки по площади смятия, при равномерно распределенной нагрузке y = 1;

R_b,loc – расчетное сопротивление бетона смятию:

,

где R_b – расчетное сопротивление тяжелого, мелкозернистого и легкого бетонов для предельных состояний первой группы на осевое сжатие, для бетона класса В12,5    R_b = 0,75 кН/см²;

a - коэффициент для расчета на изгиб, зависящий от характера опирания плит, для бетонов класса ниже В25 a =1;

 - принимают не более 2,5 для бетонов класса выше В 7,5, потому в нашем случае j _b = 2.

 кН/см².

При центрально-сжатой колонне и значительной жесткости плиты напряжения под плитой в бетоне можно считать равномерно распределенными, поэтому y = 1, тогда

см².

Считая в первом приближении плиту базы квадратной, будем иметь стороны плиты равными

см;

принимаем размеры плиты см, L = 75 cм (по конструктивным соображениям), тогда

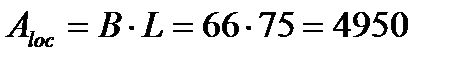см².

Напряжение под плитой

кН/см² = q.

Плита работает на изгиб, как пластинка, опертая на соответствующее число кантов (сторон). Нагрузкой является отпор фундамента. В плите имеются три участка (рис.4.13).

На участке 1 плита работает по схеме "пластинка, опертая на четыре канта". Соотношение сторон

> 2,

то есть плиту можно рассматривать как однопролетную балочную, свободно лежащую на двух опорах /1/.

Изгибающий момент:

кН×см.

Требуемая толщина плиты подбирается по максимальному изгибающему моменту, принимая материал плиты – сталь С275, для которой расчетное сопротивление R_y = 26 кН/см², тогда

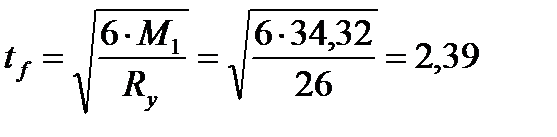см,

принимаем толщину базы 24 мм.

На участке 2 плита работает тоже, как пластинка, опертая на три канта.

см,

Соотношение сторон

,

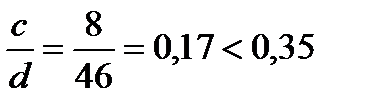следовательно, плиту можно рассматривать как консоль длиной с.

Изгибающий момент:

 кН×см.

На участке 3 плита оперта на три канта.

 см,

,

следовательно, плиту можно рассматривать как консоль длиной е.

Изгибающий момент:

 кН×см.

Рис. 4.14. База колонны (цифры в кружках - номера участков)

 

Расчет траверсы.

Считаем в запас прочности, что усилие на плиту передается только через швы, прикрепляющие ствол колонны к траверсам и не учитываем швы, соединяющие ствол колонны непосредственно с плитой базы. Траверса работает на изгиб, как балка с двумя консолями. Высота траверсы определяется из условия прочности сварного соединения траверсы с колонной.

Рассчитаем угловые швы на условный срез.

Задаемся катетом шва k_f = 13 мм.

Сварные швы будем выполнять полуавтоматической сваркой электродами Э42, выполненными из проволоки сплошного сечения Св-08А со значением 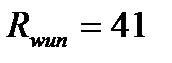кН/см². Для стали С275 значение  кН/см². Таким образом, расчетные сопротивления сварного шва по металлу шва и по границе сплавления соответственно будут равны (по табл.3 СНиП II-23-81*):

 кН/см²,

 кН/см².

Значения коэффициентов при сварке в нижнем положении равны:

 кН/см²,

 кН/см², следовательно, необходимо рассчитать сварной шов на условный срез по металлу границы сплавления. Тогда длина одного углового шва будет равна

см,

Высота траверсы h _т = l_w +1 = 44,09+1 = 45,09 см, принимаем h _т = 45 см.

4.5. Пример расчета центрально сжатой сквозной колонн

В данном примере нагрузка и длина колонны имеют другие значения, чем в п.4.4.

  Определение размеров сечения колонны

Колонна состоит из двух ветвей (два прокатных двутавра), соединенных планками.

Материал колонн – сталь С255. Для нее по табл. 51 СНиПа II-23-81* определим, что расчетное сопротивление растяжению, сжатию и изгибу по пределу текучести R_y = 24 кН/см².

В расчетной схеме имеем шарнирное крепление главных балок с колонной, и по заданию шарнирное крепление колонны к железобетонному фундаменту.

Такое крепление возможно только при условии устройства вертикальных связей между колоннами.

 

Рис.4.15. Расчетная схема колонны

Нагрузка на колонну:

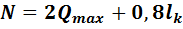
где:

- максимальная поперечная сила в главной балке, действующая на колонну.

- собственный вес колонны (0,8 – эмпирический коэффициент, учитывающий собственный вес колонны кН/м)

где:

H = 8000мм – заданная отметка верха настила,

t_н = 8мм – толщина настила в принятом варианте,

h_б.н. = 300мм – принятая по сортаменту высота балки настила,

h_гл = 1200мм – высота главной балки,

h_ф = 500мм – заглубление колонны ниже нулевой отметки.

Тогда:

1. Определяем требуемую площадь поперечного сечения стержня колонны:

где 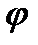 – коэффициент устойчивости, определяется по таблице СНиПа по величине .

Задаемся гибкостью колонны относительно материальной оси х в зависимости от получившейся нагрузки на колонну:

При N<2500 кН,  λ_х = 60…90.

При N≥2500 кН,  λ_х = 40…60.

Принимаем гибкость λ_х = 60.

Рис. 4.16. Поперечное сечение сквозной колонны

Условная гибкость

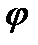Для принятого сечения (из двух двутавров) определяем тип кривой устойчивости в соответствии с типом сечения – тип «b» /1/. По таблице коэффициентов устойчивости при центральном сжатии условной гибкости  соответствует  = 0,818.

Определяем требуемую площадь поперечного сечения:

см²

Принимаем сечение колонны из двух двутавров  №33 с общей площададью

2·53,8 = 107,6 [см²], i_x = 13,5 см.

Определение требуемого расстояния между ветвями колонны

 

 Это расстояние важно для обеспечения устойчивости колонны относительно свободной оси y: чем больше расстояние, тем более устойчива колонна.

Требуемая гибкость относительно свободной оси при гибкости ветви λ_в = 30 равна:

где:

λ_х = 60 (задались)

λ_в = 30 – гибкость одной ветви колонны (задались)

Необходимый радиус инерции принятого сечения колонны относительно оси y:

где:

 - расчетная длина стержня колонны из плоскости (относительно оси y)

 (см. выше)

С помощью эмпирического коэффициента находим требуемое расстояние:

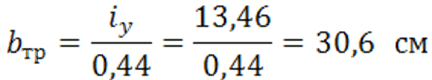
Принимаем b = 31 см

Расстояние в свету между полками двутавров

где:

b_f – ширина полки ветви колонны (по сортаменту)

a ≥ 100мм – расстояние между ветвями, которое назначается из условия возможности окраски внутренней поверхности ветви.

 

Проверка устойчивости колонны подобранного сечения.

В плоскости чертежа (относительно оси х):

Проверка по нормальным напряжениям:

где:

 - уточненный коэффициент устойчивости, который считается по истинной гибкости λ_x

 

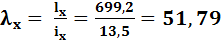
 - расчетная длина стержня колонны в плоскости х; в нашем случае

 = геометрической длине, так как имеем шарнирное крепление вверху и внизу

 = 0,859

 

Проверка устойчивости колонны относительно оси y:

 

Для определения  находим истинное

где:

 - момент инерции двух ветвей колонны;

- собственный момент инерции двутавра (сортамент)

a’ = a/2= 15,5 см – расстояние от оси у до оси у₁, проходящей через центр тяжести двутавра, параллельно оси у

 – площадь одного двутавра (сортамент)
тогда:

 

Расчет соединительных планок:

Задаемся высотой планки d = 16 см; толщиной планки t_d = 0,8 см.

 

Момент инерции сечения планки относительно собственной оси (х):

Расстояние в свету между планками:

где:  - радиус инерции сечений ветви относительно собственной оси (сортамент);  = 2,79

Приведенную гибкость определяем в зависимости от величины

где:

 - момент инерции одной ветви относительно собственной оси (у₁)

31 см - расстояние между центрами тяжести ветвей колонны.

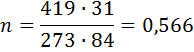
 < 5, следовательно, условная гибкость

Условно приведенная гибкость:

Тогда ϕ=

Проверка по нормальным напряжениям:

Предыдущая1234567Следующая

Поделиться:

Воспользуйтесь поиском по сайту: