 |
Среди неравномерно движущихся потоков следует отметить плавно изменяющиеся движения, характеризующееся тем, что:
|
|
|
|
· линии тока искривляются мало;
· линии тока почти параллельны, и живое сечение можно считать плоским;
· давления в живом сечении потока зависят от глубины.
Вопрос№17
Типы потоков жидкости Совокупность элементарных струек жидкости представляет собой поток жидкости. Различают следующие типы потоков (или типы движений жидкости).
Напорные потоки (напорные движения) - это такие, когда поток ограничен твердыми стенками со всех сторон, при этом в любой точке потока давление отличается от атмосферного обычно в большую сторону, но может быть и меньше атмосферного. Движение в этом случае происходит за счёт напора, создаваемого, например, насосом или водонапорной башней. Давление вдоль напорного потока обычно переменное. Такое движение имеет место во всех гидроприводах технологического оборудования, водопроводах, отопительных системах и т.п.
Безнапорные потоки (безнапорные движения) отличаются тем, что поток имеет свободную поверхность, находящуюся под атмосферным давлением. Безнапорное движение происходит под действием сил тяжести самого потока жидкости. Давление в таких потоках примерно одинаково и отличается от атмосферного только за счет глубины потока. Примером такого движения может быть течение воды в реке, канале, ручье.
Свободная струя не имеет твёрдых стенок. Движение происходит под действием сил инерции и веса жидкости. Давление в таком потоке практически равно атмосферному. Пример свободной струи – вытекание жидкости из шланга, крана и т.п.
Вопрос№18
Гидравлические характеристики потока жидкости
В гидравлике различают следующие характеристики потока: живое сечение, смоченный периметр, гидравлический радиус, расход, средняя скорость.
|
|
|
Живым сечением потока называется поверхность (поперечное сечение), нормальная ко всем линиям тока, его пересекающим, и лежащая внутри потока жидкости. Площадь живого сечения обозначается буквой S. Для элементарной струйки жидкости используют понятие живого сечения элементарной струйки (сечение струйки, перпендикулярное линиям тока), площадь которого обозначают через dS.
Смоченный периметр потока – линия, по которой жидкость соприкасается с поверхностями русла в данном живом сечении. Длина этой линии обозначается буквой c.
В напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками.
Гидравлическим радиусом R потока называется часто используемая в гидравлике величина, представляющая собой отношение площади живого сечения S к смоченному периметру c:
При напорном движении в трубе круглого сечения гидравлический радиус будет равен:
т.е. четверти диаметра, или половине радиуса трубы.
Для безнапорного потока прямоугольного сечения с размерами 
гидравлический радиус можно вычислить по формуле
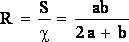
Свободная поверхность жидкости при определении смоченного периметра не учитывается
Вопрос№19
Расход потока жидкости (расход жидкости) – количество жидкости, протекающей в единицу времени через живое сечение потока. Различают объёмный, массовый и весовой расходы жидкости. Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м3/с, дм3/с или л/с. Он вычисляется по формуле
где Q - объёмный расход жидкости, V - объём жидкости, протекающий через живое сечение потока, t – время течения жидкости.
Массовый расход жид кости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле
|
|
|
где QM - массовый расход жидкости,M -масса жидкости, протекающий через живое сечение потока, t – время течения жидкости.
Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, КН/с. Формула для его определения выглядит так:
где QG - весовой расход жидкости, G - вес жидкости, протекающий через живое сечение потока, t – время течения жидкости.
Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости dQ.
Расход элементарной струйки – объем жидкости dV, проходящей через живое сечение струйки в единицу времени. Таким образом:
Если последнее выражение проинтегрировать по площади живого сечения потока можно получить формулу объёмного расхода жидкости, как сумму расходов элементарных струек
Применение этой формулы в расчетах весьма затруднительно, так как расходы элементарных струек жидкости в различных точках живого сечения потока различны. Поэтому в практике для определения расхода чаще пользуются понятием средней скорости потока.
Средняя скорость потока жидкости Vср в данном сечении это не существующая в действительности скорость потока, одинаковая для всех точек данного живого сечения, с которой должна была бы двигаться жидкость, что бы её расход был равен фактическому.
Вопрос№20
Струйная модель потока
В гидравлике рассматривается струйная модель движения жидкости, т.е. поток представляется как совокупность элементарных струек жидкости, имеющих различные скорости течения us. Индекс S означает (напоминает), что в каждой точке живого сечения скорости различны. Элементарные струйки как бы скользят друг по другу. Они трутся между собой и вследствие этого их скорости различаются. Причём, в середине потока скорости наибольшие, а к периферии они уменьшаются. Распределение скоростей по живому сечению потока можно представить в виде параболоида с основанием, равным S. Высота его в любой точке равна скорости соответствующей элементарной струйки uS. Площадь элементарной струйки равна dS. В пределах этой площади скорость можно считать постоянной. Понятно, что за единицу времени через живое сечение потока будет проходить объём жидкости Vt, равный объёму параболоида. Этот объём жидкости и будет равен расходу потока.
|
|
|
С учётом понятия средней скорости, которая во всех точках живого сечения одинакова, за единицу времени через живое сечение потока будет проходить объём жидкости (обозначим его Vtср), равный: Vtср=SVср.
Если приравнять эти объёмы Vtср = Vt=параболоида, можно определить значение средней скорости потока жидкости:
В дальнейшем среднюю скорость потока жидкости будем обозначать буквой V без индекса ср. При неравномерном движении средняя скорость в различных живых сечениях по длине потока различна. При равномерном движении средняя скорость по длине потока постоянна во всех живых сечениях.
Уравнение неразрывности жидкости. В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то можно записать:
или
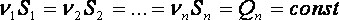
где Q— расход жидкости, м3/с; v — средняя скорость в сечении при установившемся движении, м/с; S— площадь живого сечения, м2
Как следует из вышерассмотренного уравнения расход, проходящий через все живые сечения потока, неизменен, несмотря на то, что в каждом сечении средняя скорость и площадь живого сечения различны.
Уравнение называют уравнением неразрывности потока при установившемся движении.
Из уравнения получим важное соотношение
т. е. средние скорости обратно пропорциональны площадям живых сечений, которым соответствуют эти средние скорости.
Уравнение неразрывности потока — одно из основных уравнений гидродинамики. Оно выводится из уравнения неразрывности для элементарной струйки несжимаемой жидкости при установившемся движении:
где v — местные скорости в каждом живом сечении струйки, м/с; DS — площадь живого сечения элементарной струйки, м2; D Qn— элементарный расход, м3/с
|
|
|
Рис.- схема демонстрирующая неразрывность потока
Вопрос№21
Интегрирование уравнений Эйлера возможно для двух случаев: потенциального движения ь поле сил, имеющих потенциал, и для установившегося движения (не обязательно потенциального), но также в поле сил, имеющих потенциал.
Интегрирование уравнений Эйлера возможно для ряда частных случаев течения жидкости и газа. Для удобства интегрирования представим уравнения Эйлера в иной форме. Прибавим и вычтем из левой части первого равенства сумму uyduy / dx - - uzduz / dx; второго и третьего - суммы Uxdux / dy UzdUi /
БЕРНУЛЛИ ИНТЕГРАЛ уравнений гидродинамики - интеграл, определяющий давление р в каждой точке установившегося потока идеальной однородной жидкости или баротропного газа (p = F(ρ)) через скорость v потока в соответствующей точке и через силовую функцию u(х, у, z) объемных сил:
(1)
Постоянная С имеет для каждой линии тока свое значение, меняющееся при переходе от одной линии тока к другой. Если движение потенциальное, то постоянная С для всего потока одна и та же.
Полный напор состоит из суммы приращений напоров: скоростного, пьезометрического и геометрического. В зависимости от типа рабочих органов доля преобразованного скоростного, пьезометрического и геометрического напора в полном напоре различна
Полный напор определяет энергию потока газа. Если газ рассматривать как идеальную жидкость, то энергия в каждом сечении потока будет оставаться неизменной, поскольку все реальные пазы обладают вязкостью и при движении их энергия будет убывать от сечения к сечению по направлению движения потока.
Вопрос№22
|
|
|
