 |
Турбидиметрич метод(косвенный метод).
|
|
|
|
Метод основ на измер интенс света, прошедш через сист, при услов что интенс-ть падающ свет потока ослабл в рез-те его рассеяния ДС. Iпр=I0 – Iрас. Турбидиметрию применяют для определения размеров ч-ц ДС (метод Рэлея и метод Геллера), для определения порогов коагуляции гидрозолей под действием эл-тов-коагул, для определения «защитного числа» полимеров и ПАВ по отношению к гидрозолям (стабилизирующее действие).
Метод Рэлея применим при исследов ДС, для К-ых, помимо прочих условий, выполняется соотношение d < λ.
Нефелометрический метод основан на непосредственном измерении инт-сти света, расс-ого ДС. Более высокая чувств-сть и точность этого метода по сравнению с турбид-им позволяют определять не только конц-цию и размеры ч-ц ДФ в гидрозолях, но и форму ч-ц, межчастичные взаимод-ия, а также другие св-ва ДС. В основу нефелометрии положено ур-ие Рэлея. При нефелометрии обычно используют станд золи (или градуиров-ые колоид-ые р-ры), с пом к-ых легко можно опред-ть размер ч-ц и конц-цию ч-ц ДФ в исслед золе (при пост-ой длине волны падающего света):(w-весовая конц=VνρДФ)
М-К св-ва ДС
мол-рно-кинетические св-ва (броун-кое дв-ие,диффузия, осмос и другие) ДС обусловлены тепловым дв-ем мол-л (атомов, ионов) ДСр и хар-рны только для свободнодисп-ых систем. Мол-лы жидкой и газообр ДСр находятся в непрер дв-ии и пост-но сталкиваются друг с др, проходя до столкновения расстояние, называемое средней длиной своб-ого пробега l. Величина l намного превышает размеры самих молекул (d), сильно зависит от Т:
Отклон кин энергии мол-л от ср знач, причина М-КС. Броуновское дв-ие - непрерывное, хаотическое, равновероятное для всех направлений дв-ие мелких ч-ц ДФ, взвешенных в жидкости или в газе, за счет воздействия мол-л ДСр. диффузия - самопроизвольное распростр-е в-ва из обл с большей конц-цией в обл с меньшей конц-цией,приводящее к выравниванию конц-ции в-ва в системе. Разл молекулярную диффузию, ионную диффузию и диффузию коллоидных ч-ц. Осмосом- При разделении двух р-ров с разл конц-цией полупроницаемой перегородкой возникает поток р-ля, направленный от более разбавл-ого к б. концентриров-ому р-ру, приводящий к выравниванию конц-ции р-ого в-ва в обоих р-рах.
|
|
|
Седиментация -процесс оседания или всплывания ч-ц ДФ в ДС, обусловленный различиями в плотностях ДФ и ДСр.
Броуновское движение
- непрерывное, хаотическое, равновероятное для всех направлений движение мелких частиц дисперсной фазы, взвешенных в жидкости или в газе, за счет воздействия молекул дисперсионной среды.
Крупн частицыДФ чаще сталкивыются,но остаеся непродвижными. БД хара-но для высокодисп сист(они маленькие). Т.к чатицы часто меняют свое направл, то за БД принимают не путь в единицу времени, а сдвиг одной частицы в простр-ве:
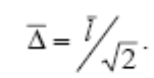
Средн сдвиг чатсиц ДФ:
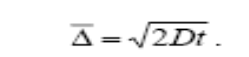А. Эйнштейн и М. Смолуховский постулировали единство природы броуновского движения частиц дисперсной фазы и теплового движения молекул ДСр, установили количественную связь между средним сдвигом частиц ДФ (амплитудой смещения) и коэффициентом диффузии D частиц дисперсной фазы.
При выводе уравнения Эйнштейна–Смолуховского были приняты след допущения: частицы ДФ движутся независимо друг от друга и между ними отсутствует взаимод-ие, средняя энергия поступательного движения частиц в одном направлении составляет kT /2.
Теория броуновского движения исходит из представлений о взаимодействии случайной силы f (t), которая характеризует удары отдельных молекул ДСр, силы Ft (равнодействующей), зависящей от времени, и силы трения при движении частиц ДФ в дисперсионной среде со скоростью ϑ. Уравнение случайного броуновского движения (закон Ланжевена) в диф-ой форме имеет вид:
|
|
|
Если рассматривать эволюцию системы за длительный промежуток времени, то t >> m / η, инерцией частиц ДФ (md ϑ / dt) можно пренебречь, и уравнение Ланжевена принимает вид ηϑ = Ft + f (t) Величина среднего сдвига частиц ДФ возрастает с ростом температуры, уменьшением вязкости дисперсионной среды и размера частиц ДФ броуновское движение наиболее ярко выражено для высокодисперсных (ультрамикрогетерогенных) систем, а его интенсивность сильно зависит от дисперсности. Для среднедисперсных (микрогетерогенных) систем средний сдвиг невелик и составляет порядка 1 мкм.Для грубодисперсных (макрогетерогенных) систем (частицы размером более 10 мкм) броуновским движением можно пренебречь.
54 Диффузия
диффузия - самопроизвольное распростр-ие в-ва из области с большей конц-цией в область с меньшей концентрацией,приводящее к выравниванию концентрации вещества в системе. Различают молекулярную диффузию, ионную диффузию и диффузию коллоидных частиц. (Физический смысл диффузии – количество вещества, переносимое через единицу площади в единицу времени при единичном градиенте концентрации.)
Явление диффузии описывают при помощи законов Фика. Если диффузия вещества протекает при постоянстве градиента концентраций в системе dc / dx ≠ f (T) = const, то говорят о стационарной диффузии, если градиент концентраций реагентов изменяется с течением
времени dc / dx = f (T) ≠ const, то диффузия явл-ся нестацион первый и второй закон Фика для одномерной диффузии (в направлении оси x):
J – поток диффузии, показывающий, какое количество вещества проходит (диффундирует) через поперечное сечение единичной площади за единицу времени, моль / (м2 · с) (кг / (м2 · с) или частиц / (м2 · с)); D – коэффициент диффузии, м2/с; c – молярн концентрация диффундирующего реагента, моль/м3.
где k – постоянная Больцмана, T – абсолютная температура, B – коэффициент трения,
средний сдвиг частиц ДФ (для данной дисперсной системы (B = const)) зависит только от температуры и времени фиксации сдвига. Интересно отметить, что скорость среднего сдвига частиц ДФ зависит от промежутка времени между измерениями расстояния, на которое переместилась частица, и уменьшается с ростом этого промежутка времени.
|
|
|
подобно броуновскому движению, диффузия в полной мере проявляется в ультрамикрогетерогенных (высокодисперсных) системах, ослаблена в микрогетерогенных (среднедисперсных) и практически отсутствует в макрогетерогенных (грубодисперсных) системах
55.Осмотич давление.
При разделении двух растворов с различной концентрацией или раствора и чистого растворителя полупроницаемой перегородкой (мембраной) возникает поток растворителя, направленный от раствора с меньшей концентрацией растворенного вещества к раствору с большей концентрацией этого вещества (поток растворителя от более разбавленного к более концентрированному раствору), приводящий к
выравниванию концентрации растворенного вещества в обоих растворах. Этот процесс называется осмосом‡. Осмос представляет собой одностороннюю диффузию (через полупроницаемую мембрану) молекул растворителя (для истинных растворов)или дисперсионной среды (для дисперсных систем).Если разместить сосуд с более разбавленным раствором под вторым (с более концентрированным раствором), то в результате перемещения жидкости через полупроницаемую мембрану в верхний сосуд в нем создается избыточное давление осмотическое. П еренос растворителя в верхний сосуд будет происходить до тех пор, пока гидростатическое давление столба жидкости в верхнем сосуде полностью не компенсирует осмотическое давление растворителя
Таким образом, если переносу вещества в результате осмоса не препятствуют (способствуют) какие-либо силы (силы тяжести при горизонт расположении сосудов), то концентрация в контактирующих сосудах выравнивается полностью, если препятствуют (способствуют) (силы тяжести при вертикальном расположении сосудов), то концентрация выравнивается лишь частично.
Осмотическое давление (π) может быть определено при помощи уравнения Вант-Гоффа, которое для молекулярных растворов имеет вид:π = cRT
|
|
|
В растворах электролитов общее число частиц растворенного вещества превышает число молекул (вследствие диссоциации молекул),что учитывают, вводя в уравнение Вант-Гоффа изотонический коэффициент (i): i = 1 + α(ν – 1),
Для разбавленных растворов слабых электролитов уравнение Вант-Гоффа: π = icRT
Для дисперсных систем осмотическое давление выражается уравнением Вант-Гоффа в виде:
 |
56.Седиментация частиц ДФ.
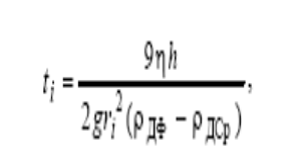
СедиментациЯ -процесс оседания или всплывания ч-ц ДФ в ДС, обусловл различиями в плотностях ДФ и ДСр. Оседание частиц ДФ (при ρДФ > ρДСр) наз-ся прямой, а всплывание (при ρДФ < ρДСр) – обратной седиментацией. На покоящуюся частичку ДФ в ДСр действует две силы: сила Архимеда (FA) и сила тяжести (Fg): FA = V ρДСр g, Fg = V ρДФ g, отсюда F сед = Fg – FA = V (ρДФ – ρДСр) g. Прямая седимент происх при усл, что F сед > 0 (Fg > FA), в обратная – F сед < 0 (Fg < FA). При ламинарном дв-ии ч-ц ДФ в ДСр возникает сила сопротивл (тр) F тр, замедл-ая их дв-ие: F тр = B ϑ, где B – коэф-т тр, ϑ – скор седим-ции ч-ц. F = F сед – F тр = V (ρДФ – ρДСр) g – B ϑ.
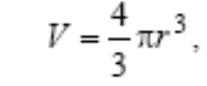В нач момент дв-ия ϑ мала и ч-ца движ ускоренно; при ув-ии скорости седиментации растет сила тр и при достаточно большом значении коэф-та трения наступает момент, когда сила тр станов равна силе седиментации, равнод-щая этих сил равна нулю (F = 0), скорость седиментации ч-цы станов постоянной и равной:
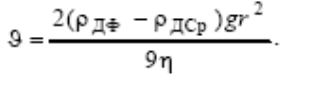з-на Стокса: B = 6πη r,
выражение для скорости се-
диментации примет вид:
По изв скорости седиментации ч-ц ДФ опред их радиус:
Для ускорения процесса седиментацию ч-ц ультрамикрогетерогенных систем часто проводят не в гравитационном, а в центробежном поле (в центрифуге). В этом случае радиус частиц рассчитывают по формуле:
Седиментационный метод анализа в гравитационном поле применим для анализа микрогетерогенных и некоторых грубодисперсных систем Чтобы уравнение седиментации отдельной ч-цы было применимо для всей сов-сти частиц, должно выполняться условие независимости дв-ия каждой ч-цы. Это условие достигается в разбавл системах; иногда в систему необходимо дополнительно вводить стабилизаторы, препятствующие слипанию ч-ц.
Монодисперсные- размеры ч-ц ДФ (дисперсность) одинаковы и все ч-цы оседают с одинаковой скоростью.
Найдя эту скорость в любой момент времени, можно легко определить размер ч-Ц. mt-масса осадка
В полидисп системах ч-цы имеют разные размеры (дисперсность) и оседают с разл скоростью. В основу дисперс-ого седиментац-ого анализа полидисп-ых систем положено Предст-ие о том, что системы состоят из неск-их фракций, к-ые можно рассм-ть как отдельные монодисперсные системы.
|
|
|
При седиментационном анализе полидисп-ых систем вначале определяют время полного оседания частиц отдельных фракций после чего графически или аналитически определяют массу этой фракции в системе в целом (mi).
Математ обработку седиментационной кривой проводят при помощи уравнения Одена:
где m – масса ДФ, осевшей к моменту t; mi – масса фракций ч-ц ДФ, полностью осевших к моменту t.
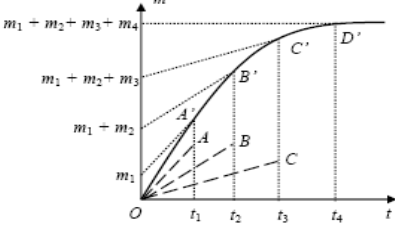
Отрезки OA, OB, OC описывают оседание отдельных фракций; при этом, чем
меньше наклон прямой, тем меньше размер частиц в этой фракции. Закончив анализ системы, строят дифференциальную и интегральную кривые распределения частиц по размерам
При помощи кривых распределения можно определить дисперсность и степень полидисперсности системы, средние значения радиуса, объема и массы частиц дисперсной фазы, удельную поверхность системы и многие другие. чем на большее число фракций будет разбита полидисперсная система, тем в большей степени эти фракции будут соответствовать монодисперсным системам и тем более корректным будет описание системы в целом.
Седимент анализ.
В полидисперсных системах частицы имеют разные размеры (дисперсность) и оседают с различной скоростью. В основу дисперсионного седиментационного анализа полидисперсных систем положено
представление о том, что системы состоят из нескольких фракций, которые можно рассматривать как отдельные монодисперсные системы. При седиментационном анализе полидисперсных систем вначале определяют время полного оседания частиц отдельных фракций
после чего графически или аналитически определяют массу этой фракции в системе в целом (mi).
Математическую обработку седиментационной кривой проводят при помощи уравнения Одена:
где m – масса ДФ, осевшей к моменту времени t; mi – масса фракций частиц ДФ, полностью осевших к моменту времени t. В уравнении Одена предполагается, что частицы отдельных фракций оседают независимо друг от друга. m = (k 1 + k 2 + k 3 + k 4) t, m = m 1 + (k 2 + k 3 + k 4) t, m = (m 1 + m 2) + (k 3 + k 4) t, m = (m 1 + m 2 + m 3) + k 4 t,
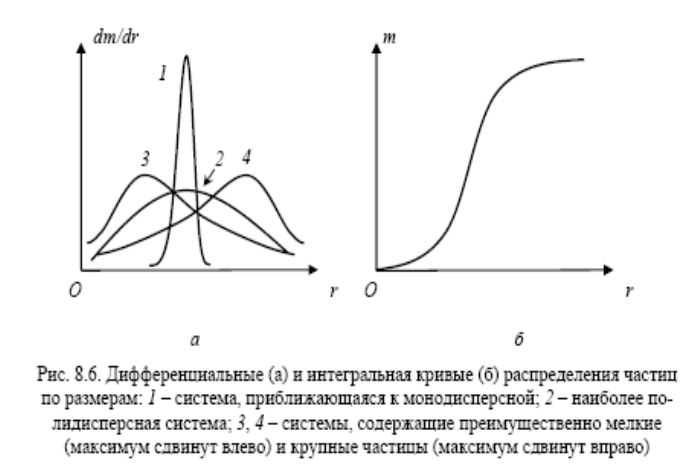Отрезки OA, OB, OC описывают оседание отдельных фракций; при этом, чем меньше наклон прямой, тем меньше размер частиц в этой фракции. Закончив анализ системы, строят дифференциальную и интегральную кривые распределения частиц по размерам. При помощи кривых распределения можно определить дисп-сть и степень полидиспер-сти системы, сред значения радиуса, объема и массы ч-ц ДФ, уд пов-сть системы и многие др. полидисп-сть систем чаще всего характеризуют отношением среднечисл-го значения того или иного параметра системы к среднемассовому:
Меньше 1, чем меньше,тем> полидисп.
чем на большее число фракций будет разбита полидисп система, тем в большей степени эти фракции будут соответ монодисп сист и тем более корректным будет описание системы в целом.
СЕдимент-диффузн
Седиментации частиц в дисперсных системах должна противодействовать их диффузия. мы должны учитывать наличие в системе двух потоков: седиментационного (I сед), в результате которого происходит постепенное разделение дисперсной системы на отдельные фазы (дисперсную фазу (ДФ) и дисперсионную среду (ДСр)), и диффузионного (I диф), приводящего к выравниванию концентрации частиц ДФ по всему объему дисперсионной среды:
(v -частичная конц.)
В грубодисперсных (макрогетерогенных) системах I сед > I диф, поэтому для них характерна седиментация и нехарактерна диффузия; с течением времени все частицы дисперсной фазы таких систем концентрируются в одной области дисперсной системы, в результате чего рано или поздно происходит пространственное разделение фаз.
В ультрамикрогетерогенных (высокодисперсных) системах I сед < I диф, поэтому для них нехарактерна седиментация и характерна диффузия; в таких системах за счет диффузии частицы ДФ равномерно распределяются по всему объему дисперсионной среды. В микрогетерогенных (и некоторых ультрамикрогетерогенных) системах интенсивность седиментации и диффузии близки, вследствие чего с течением времени в таких системах происходит выравнивание диффузионного и седиментационного потоков I сед = I диф:
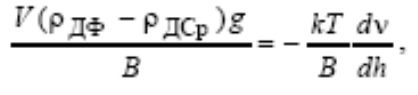устанавливается седиментационное-диффузионное равновесие, описываемое гипсометрическим законом Лапласа:показывает, как измен-ся конц-ция ч-ц в ДС в зав-сти от расстояния от дна сосуда.
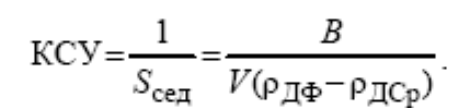Мерой кинетической седиментационной устойчивости (КСУ) дисперсных систем к оседанию является величина, обратная константе седиментации:
если сферическая
ТД седиментационная устойчивость (ТСУ) ДС обусловл статистич з-ами диффузии и непосредст-но связана с Седиментационно-диффузионным равновесием. Мерой ТСУ является гипсометрическая высота, т.е. высота, на которой концентрация частиц дисперсной фазы снижается в e раз:
Электрокинет явл.
Для дисперсных систем с заряженными частицами ДФ характерно наличие т. н. электрокинетических явлений. По причинно-следственной связи все электрокинетические явления делят на прямые и обратные.
К прямым электрокинетическим явления относят явления, при которых движение одной фазы дисперсной системы относительно другой происходит вследствие помещения системы в электрическое поле (вызвано разностью потенциалов в системе). Прямыми электрокинетическими явлениями являются электрофорез и электроосмос.
К обратным электрокинетическим явлениям относят явления, при которых движение одной фазы дисперсной системы относительно другой вызывает возникновение в системе разности потенциалов (электрического поля). Обратными электрокинетическими явлениями являются потенциал течения и потенциал седиментации.
В соответствии с тем, что движется (дисперсная фаза или дисперсионная среда), парными явлениями являются электрофорез и потенциал седиментации (в обоих явлениях происходит движение частиц дисперсной фазы относительно неподвижной дисперсионной среды), электроосмос и потенциал течения (в обоих явлениях происходит движение дисперсионной среды относительно неподвижной дисперсной фазы).
60. Электрофорез.
Под электрофорезом понимают явление перемещения заряж ч-ц ДФ относительно неподвижной ДСр под действием внешнего электрич поля к одному из эл-дов.
Электрофорез может происх только в седиментационно уст-вых ультрамикрогетерогенных или микрогетерог-ых Свободнодисп-ых системах с жидкой или газообр ДСр.
В своих опытах Рейсс погружал во влажную глину две стеклянные трубки, заполненные водой и опускал в каждую из трубок по электроду. При наложении на электроды разности электрических потенциалов он наблюдал, как жидкость в трубке с положительно заряженным электродом мутнела, а в трубке с отрицательно заряженным электродом оставалась прозрачной.Т.о., происходило перемещ ч-ц ДФ к положительно заряженному электроду. Появление мути в левой трубке можно объяснить след образом. Под действием внешнего электрического поля происходит разрыв ДЭС в стр-ре ч-ц ДФ по плоскости скольжения, вследствие чего отрицательно заряженные ч-цы глины приобретают способн двигаться к положит-ому электроду.
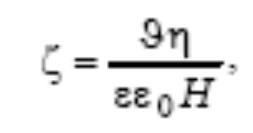Зная линейную скорость движения коллоидных частиц ϑ в электрическом поле, величину электрокинетического потенциала ζ можно рассчитать по уравнению Гельмгольца-Смолуховского:
В макроэлектрофорезе за величину линейной скорости движения
коллоидных частиц принимают скорость движения границы раздела «золь – контактная жидкость».1 в стакан с водой доб 20%-р-р K4[Fe(CN)6],затем по каплям доб Fecl3. U-образная трубка наполовину заполнена водой.в верхнее отверствия вставл электроды. Получ р-р берл лазури налив в емкость,при остор открыт крана золь переходит из емкости в нижнюю часть трубки,уровень воды в обоих коленях повышается, кран закр, когда трубка заполн золем наполовину(измеряем расстояние между электродами).затем подают пост напряжение и засекают время начала. Под действ эл поля граница «золь-вода» начин перемещ-ся(в одном колене поднимается, в др - опускается).через час источн тока отключ. Среднее 
смещение находят по ф-ле:
Далее, при помощи уравнения Гельмгольца–Смолуховского рассчитывают величину электрокинетического
потенциала исследуемого гидрозоля. Знак ζ-потенциала определяется тем, к какому электроду смещается граница раздела фаз «золь –контактная жидкость»: если к положительному, то коллоидные частицы заряжены отрицательно, и наоборот.
Электроосмос
Под электроосмосом понимают дв-ие жидкой ДСр относительно твердой неподвижной дисперсной фазы под действием внешнего электрического поля.
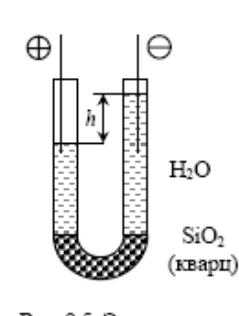U-образная трубка, которая была перегорожена в нижней части диафрагмой из кварцевого песка и заполнена обычной водой. При наложении на систему электрического поля обнаруживалось перемещение жидкости в то колено трубки, в которое был помещен отрицательно заряженный электрод. Перемещение происходило до тех пор, пока в коленах трубки не устанавливалась постоянная разность уровней h, после чего дальнейшее поднятие уровня жидкости уже не наблюдалось. В контрольном опыте (без диафрагмы в средней части трубки) перемещения жидкости не наблюдалось, из чего Рейсс сделал вывод о том,жидкость заряжается при контакте с частицами кварца (SiO2).
Явление электроосмоса можно объяснить тем, что под действием внешнего электрического поля подвижные гидратированные противоионы диффузной части ДЭС двигаются к противоположно заряженному электроду, увлекая за собой молекулы дисперсионной среды (воды). Движение заряженного слоя передается соседним слоям незаряженной жидкости, и за счет внутреннего трения возникает движение массы (объема) жидкости. При описании электроосмоса линейную скорость перемещения дисперсионной среды обычно заменяют объемной скоростью течения жидкости, которая достаточно легко определяется экспериментально.
объемная скорость перемещения жидкости в пористом теле под действием электрического поля пропорциональна силе тока, протекающего через систему, а отношение объемной скорости к силе тока есть постоянная величина, не зависящая от площади сечения и толщины пористой диафрагмы. Расчет электрокинетического потенциала при определении его электроосмотическим методом проводят по уравнению Гельмгольца–Смолуховского, которое для явления электроосмоса имеет следующий вид:
 |
Потенциал течения
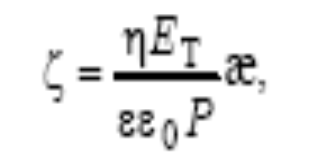Квинке установил, что при течении ж-сти ч-з пористое тело под действием внешн давл в сист возникает разность потенциалов Эта разность потенциалов возникала при теч воды и водных растворов разл в-в ч-з пористые материалы разл природы (глина, песок, древесина, графит и др.). Обнаруженное Квинке явление получило название потенциала течения (или потенциала (эф-та) Квинке). Впоследствии было установлено, что величина потенц течения не зависит от толщ и площади попер-ого сечения диафрагмы и кол-ва фильтруемой (протекающей через пористую диафрагму) жидк, однако, как и при электроосмосе, пропорц объемной скорости жидк. Итак, потенциал течения – это разность потенц, возникающая при продавливании (при течении) ДСр через пористую перегородку под действием внешн давл. Появление потенц теч обусловлено тем, что поток жидк, двигающийся по капиллярам пористой перегородки под действ внешн давл Р, увлекает за собой ПИ диффузной части ДЭС, слабо удерживаемые стенками капилляров. В рез-те дв-ия ионов вдоль пов-сти пор возн пов-ый ток, а также разность потенциалов на концах диафрагмы (Е Т), к-ую можно экспер-но измерить. Ур-ие Гельмг-Смолух для расчета ζ-потенциала при помощи потенц теч (Е Т) имеет вид: значения η и ε могут значит отличаться от справочных, характеризующих изотропную жидк; это различие станов весьма ощутимым, если толщ ДЭС и радиус капил-ов пористого тела, ч-з к-ые осущ-ся течение ж-сти, станов соизмеримыми. Поэтому применение потенц теч для определения ζ ограничено.
Потенциал седиментации
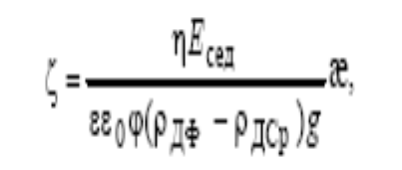Дорн измерил разность потенциалов, возникающую при оседании ч-ц суспензии кварца в центробежном поле. Явление возникн разности потенциалов при оседании ч-ц ДФ(в гравитационном или центробежном поле) получило название потенциала оседания (седиментации) (или потенциала (эффекта) Дорна). При оседании ч-ц кварца гидратированные ПИ диффузной части ДЭС отстают от движущейся ч-цы вследствие действия сил тр м-у ними и мол-ами воды. В рез-те происходит разделение зарядов в системе, и возникает разность потенциалов. Подобный эффект наблюдается как в гравитац-м поле, так и в поле центробежной силы при центрифугировании суспензий. В последнем случае этот эффект выражен значительно сильнее, поскольку в цетрифугах можно достичь ускорений в десятки и сотни g. Связь между потенциалом седиментации (Е сед) и электрокинетическим потенциалом (ζ) ч-ц выражается ур-ем Гельмгольца–Смолуховского в виде:
ϕ – объемная доля ДФ
Погрешности в определении ζ-потенциала:определении электрокинет-ого потенциала другими способами: в ур-ие Гельмгольца–Смолуховского приходится подставлять хар-ки ДСр в целом (вязкость, диэлектрическую проницаемость и ЭП), а не их значения на плоскости скольжения (в месте разрыва ДЭС).
64.Суспензии.
Суспензии предст собой ДС, в к-ых ДФ образуют ч-цы тв тела с размером более сотни нанометров, а ДСр явл-ся ж-сть, чаще всего – (вода). суспензии предст собой ДС типа Т/Ж (иногда суспензии наз взвесями порошков в ж-тях).
для суспензий практически не выражены броун-кое дв-ие и диффузия, однако весьма характерно явление седиментации (в суспензиях с оч мелкими размерами ч-ц устанавл-ся седиментационно-диффузионное равновесие).
В зав-сти от природы ДСр: водные суспензии (ДСр –вода) и органосуспензии (ДСр – любая орг-ая жидкость). В зав-сти от размеров частиц ДФ: грубые (10–4 м < d), тонкие (5·10–7 м < d < 10–4 м) и мути (10–7 м < d < 5·10–7 м).
В зав-сти от конц-ции ч-ц ДФ: разбавлсуспензии (взвеси) и концентрированные суспензии(пасты). Взвеси предст собой свободно-, а пасты – связнодисперсные системы.
Суспензии получают двумя осн-ыми способами – диспергационным и конденсационным. В первом случае либо крупные ч-цы ДФ измельчают непосредственно в ж-сти либо смешивают порошки с ДСр (например, водой); при этом образов взвеси происх по схеме: Т/Г + Ж = Т/Ж,
Получение суспензий конденсац-ыми методами аналог получению золей, но образующиеся в процессе конденс ч-цы ДФ имели достат крупн размер (10–7 м< d). Этого добиваются разл-ыми способ:например,сливая не разбавл, а концентриров-ые р-ры, или проводя процесс т.о., чтобы обр-ие ч-ц ДФ проходило при малых степенях пересыщ р-ра в-вом ДФ(им-но в этом случае обр-ся крупн ч-цы).
Разбавл-ые суспензии (взвеси) проявляют разнообр св-в.
К оптич св-вам суспензий относ-ся поглощ и отраж света; светорас-ие - для мутей, Ч-цы ДФ в грубых и нек-ых тонких суспензиях достат велики и могут наблюд в обычный оптич микроскоп. Из мол-рно-кинетич св-в для большинства суспензий наиб выражена седиментация; броун-кое дв-ие и диффузия в них проявл-ся слабо вследствие большого размера ч-ц. Вместе с тем, в мутях, а также близких к ним по размерам ч-ц ДФ тонких суспензиях (d ≈ 10–7–10–6 м) вследствие интенс тепловых конвекционных потоков, препятствующих оседанию ч-ц ДФ, устанавливается диффузионно-седиментационное равновесие.
Электрокинетические св-ва суспензий аналог св-вам гидрозолей; при этом величина ζ практически важных сусп варьируется в пределах от –100 до50 мВ*. (электроосмос или потен седиментация). Вязкость взвесей (низкоконцентрированных свободнодисп-ых систем) определяется, гл. образом, вязкостью ДСр, к-ая, в зав-сти от природы образующих ее в-тв, Введение в систему ч-ц
ДФ приводит к возрастанию ее вязкости. Возрастание вязкости, вызванное наличием таких слоев, называют соотв-но адсорбц-ным, сольватным и электровязкостным эффектом. вязкость в системе должна расти с ув-ем дисперсности системы. Электровязкостный эффект можно уменьшить при введении в сист электролитов, приводящих к сжатию ДСПИ и к уменьш электрокин-ого потенциала.
(при высоких концентрациях) становится особенно заметной роль стабилизирующих слоев на пов-сти ч-ц ДФ. Пов-ые слои соседних ч-ц перекрываются, что приводит к резкому росту сил отталкивания. При определенных услових силы притяж и отталк м-у ч-цами становятся равны, а при дальнейшем ув-нии конц-ции ч-ц ДФ способствует росту этих сил при сохранении их равенства.
В агрегативно уст-вых суспензиях оседание ч-ц происх медл и формируются плотные осадки. Распределение ч-ц ДФ по объему осадка определяется соотнош м-у силой тяжести, молекулярным притяж ч-ц и силами отталкивания м-у ч-цами.В агрег неуст-вых суспензиях оседание ч-ц ДФ происх значит-но быстрее вследствие обр-ия агрегатов. Образующиеся в этом случае осадки явл неплотными, а зачастую –рыхлыми. Для достижения агрегативной уст-сти суспензий необх-мо выполнение хотя бы одного из усл:
1) смачиваемость пов-сти ч-ц ДФ дисперсионной средой;
2) наличие в системе стабилизатора.(ПАВ(адсорбционно-сольватный фактор устойчивости),ВМС) сенсибилизация под действием ВМС(умееньш агрегат уст-ти)
|
|
|
