 |
Вычисление пределов последовательностей.
|
|
|
|
Математический анализ
Множества.
Множество – это совокупность однородных объектов, называемых элементами.
Множества могут состоять из чисел, векторов, функций и других объектов.
Множества обозначаются прописными буквами – А, В, С,, а их элементы строчными - буквами a, b, c.
Если элемент a принадлежит множеству А, то это обозначается как  , если элемент a не принадлежит множеству А, то это обозначается
, если элемент a не принадлежит множеству А, то это обозначается  .
.
Множество, не содержащее ни одного элемента, называется пустым и обозначается 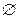 .
.
Множество В называется подмножеством множества А, если все элементы множества В принадлежат множеству А. Это обозначается как операция включения: 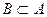 .
.
Множества называются равными, если их элементы равны.
Объединением множеств А и В называется множество С, если элементы которого принадлежат или А, или В, или обоим множествам, то есть, хотя бы одному из данных множеств 
Пересечением множеств А и В называется множество D, состоящее из элементов, одновременно принадлежащих и множеству А и множеству В  .
.
Разностью множеств А и В называется множество Е,состоящее из всех элементов множества А, не принадлежащих множеству В  .
.
Множества, элементами которых являются действительные числа, называются числовыми.
Числовые последовательности.
Числовой последовательностью называется бесконечное множество вещественных чисел, следующих друг за другом и связанных между собой зависимостью от НОМЕРА в последовательности.

Числа  называются элементами, или членами последовательности.
называются элементами, или членами последовательности.
 - первый член последовательности,
- первый член последовательности,
 - общий член последовательности.
- общий член последовательности.
Последовательность обозначается как  .
.
Например, если дана последовательность 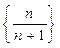 , то она имеет вид
, то она имеет вид
|
|
|
 , т.к. при
, т.к. при
 и т.д.
и т.д.
Последовательность  можно представить в виде
можно представить в виде 
Последовательность  записывается в виде
записывается в виде 
Общий вид последовательности часто нужно определить по ее общему члену.
Пример. Если последовательность задана как  , то общий член равен
, то общий член равен

Предел последовательности.
Пределом последовательности называется число А, если для любого положительного, сколь угодно малого числа  существует такой номер элемента N, что для всех последующих номеров
существует такой номер элемента N, что для всех последующих номеров  выполняется неравенство
выполняется неравенство
 ,
,
то есть все следующие элементы последовательности будут отличаться от предела А на величину, меньшую, чем  .
.
Последовательность, имеющая предел, называется сходящейся.
Предел последовательности обозначается так:

Очевидно, что члены последовательности  стремятся к нулю, при
стремятся к нулю, при 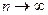 (чем на большее число производится деление, тем меньший результат получается),
(чем на большее число производится деление, тем меньший результат получается),
то есть
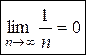
Очевидно так же, что последовательности 

 и т.п. тоже имеют предел, равный нулю.
и т.п. тоже имеют предел, равный нулю.
Последовательности, предел которых равен нулю, 
называются бесконечно малыми.
Последовательности, не имеющие конечных пределов, 
называются бесконечно большими.
Если последовательность  - бесконечно малая, то последовательность
- бесконечно малая, то последовательность  является бесконечно большой.
является бесконечно большой.
Вычисление пределов последовательностей.
*** При вычислении пределов при 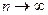 нужно пользоваться известным пределом бесконечно малых последовательностей
нужно пользоваться известным пределом бесконечно малых последовательностей 
 и т.п.
и т.п.
Заданные последовательности нужно приводить к бесконечно малым последовательностям - привести возможные элементы числителя и знаменателя последовательности к бесконечно малым вынесением за скобки наибольшей степени многочлена.
Пример 1. Вычислить предел последовательности 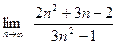

так как 

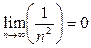
Пример 2. Вычислить предел последовательности 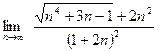
Вынесение наибольшей степени многочлена и приведение к бесконечно малым можно проводить внутри степени (и корня).
|
|
|

Пример 3.  ,
,
потому что функция  является убывающей, так как это показательная функция с основанием
является убывающей, так как это показательная функция с основанием  , то есть
, то есть 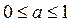 . Следовательно,
. Следовательно, 
Пример 4. Вычислить предел последовательности 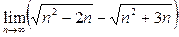
Предел представляет собой неопределенность  .
.
Для того, чтобы от нее избавиться, нужно произвести избавление от иррациональности.
** Из алгебры известно, что 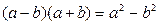
Если в качестве элементов 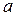 и
и  используются корни, то формула принимает вид:
используются корни, то формула принимает вид:

Таким образом, чтобы избавить выражение от корня, нужно умножить его на выражение, с аналогичными элементами, но с противоположным знаком. Такое выражение называется сопряженным. Чтобы последовательность не изменилась, нужно на такое же выражение последовательность разделить.

Очевидно, что в числителе можно избавиться от корней и преобразовать полученное выражение

В знаменателе выполняются действия так же, как и в примере 2.

|
|
|


