|
Задания для самостоятельной работы
|
|
|
|
1. Записать первые пять членов последовательностей:
1) 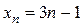 2)
2)  3)
3)  4)
4)  5)
5) 
6)  7)
7)  8)
8) 
2. Определить общий член последовательности по ее первым элементам:
1) 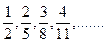 2)
2) 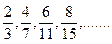 3)
3)  4)
4) 
3. Вычислить значения пределов последовательностей:

9)  10)
10)  11)
11)  12)
12) 
13) 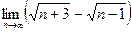 14)
14)  15)
15) 
16) 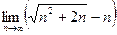 17)
17)  18)
18) 
Понятие функции
Есть каждому значению из множества Х ставится в соответствие множество значение из множества У, то задается функция У от Х.
Функцией называется однозначная зависимость переменной У от переменной Х.
При этом переменная Х - независимая переменная и называется аргументом.
!!! В качестве функций могут рассматриваться различные зависимости – зависимость спроса от цены продукции, цены товара от предложения, скорость движения тела от времени, значения давления в газе от температуры и так далее.
Способы задания функции:
· аналитический – представление функции в виде формулы 
· табличный – зависимость У от Х задается в виде таблицы значений

| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 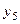
| 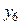
| 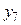
|
· графический – наглядное отображение зависимости У от Х задается в виде графика в системе координат
Предел функции в точке.
Представим функцию  в графическом виде
в графическом виде







 |












 |
0





 |

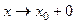
слева справа
Рассмотрим последовательность значений  ,
,  ,
,  , предел которой сходится к
, предел которой сходится к
значению  .
.
Им соответствуют значения функции, которые тоже составляют последовательность
 , сходящуюся к
, сходящуюся к  .
.
Определение предела по Гейне:
Пределом функции  в точке
в точке 

(или пределом функции при  ) называется значение А,
) называется значение А,
если к значению А стремится предел последовательности  , элементы которой соответствуют последовательности
, элементы которой соответствуют последовательности  , пределом которой является значение
, пределом которой является значение 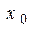 .
.
|
|
|

При этом последовательность  может стремиться к
может стремиться к  от меньших значений
от меньших значений
при 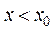 – слева – предел СЛЕВА
– слева – предел СЛЕВА 
И от больших значений - при  – справа – предел СПРАВА:
– справа – предел СПРАВА: 
Условие существования предела функции в точке.
Функция  имеет предел в точке
имеет предел в точке  только тогда, если существуют пределы слева и справа и их значения равны.
только тогда, если существуют пределы слева и справа и их значения равны.
Определение предела по Коши:
Число А называется пределом функции 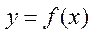 при х, стремящихся к
при х, стремящихся к  (
(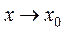 ), если для любого, сколь угодно малого числа положительного числа
), если для любого, сколь угодно малого числа положительного числа  (
(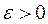 ) существует такое число
) существует такое число  , что для всех х, удовлетворяющих условию
, что для всех х, удовлетворяющих условию  выполняется неравенство
выполняется неравенство 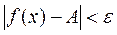 ,
,
Свойства пределов функций и последовательностей.
- Функция не может иметь более одного предела
Вычисление пределов функций.
*** При вычислении пределов при  нужно подставить значение
нужно подставить значение  в заданную функцию.
в заданную функцию.
При определении пределов отношения обычно возникают НЕОПРЕДЕЛЕННОСТИ




Их нужно раскрыть с помощью преобразования функции.
Пример 1. Вычислить предел функции 
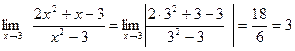
Пример 2. Вычислить предел функции 
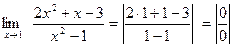
В результате подстановки возникла неопределенность 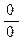 , которую нужно раскрыть, преобразовав функцию.
, которую нужно раскрыть, преобразовав функцию.
Для этого используются формулы сокращенного преобразования и разложение квадратного трехчлена с помощью определения его корней:

Разложение на множители квадратного трехчлена определяется по формуле:
 ,
,
где  и
и 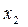 - корни уравнения
- корни уравнения  , вычисляемые по формуле
, вычисляемые по формуле

Исходя из этого, получаем,

Пример 3. Вычислить предел функции 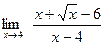
Очевидно, что при подстановке  возникает неопределенность
возникает неопределенность  , которую нужно раскрыть, используя алгебраические преобразования, дополнив их действием замены переменной:
, которую нужно раскрыть, используя алгебраические преобразования, дополнив их действием замены переменной:
Пусть  , следовательно,
, следовательно,  . Тогда числитель и знаменатель принимают вид выражений, которые легко раскладывается на множители:
. Тогда числитель и знаменатель принимают вид выражений, которые легко раскладывается на множители:
|
|
|


Возвращаясь к первоначальной переменной, нужно записать 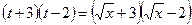
Действия в знаменателе выполняются аналогично:
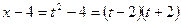
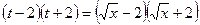
Подстановка в предел функции полученных выражений, приводит к следующему

Очевидно, что одинаковые множители в числителе и знаменателе можно сократить и затем подставить в функцию значение, к которому стремится х - 

|
|
|