 |
Нормальное уравнение прямой.
|
|
|
|
Если обе части уравнения Ах + Ву + С = 0 разделить на число 
, которое называется нормирующем множителем, то получим xcosj + ysinj - p = 0 – нормальное уравнение прямой.
Знак ± нормирующего множителя надо выбирать так, чтобы m×С < 0.
р – длина перпендикуляра, опущенного из начала координат на прямую, а j - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение этой прямой в отрезках: 
уравнение этой прямой с угловым коэффициентом: (делим на 5)
нормальное уравнение прямой:
; cosj = 12/13; sinj = -5/13; p = 5.
Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.
Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.
Уравнение прямой имеет вид: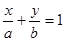 
, a = b = 1; ab/2 = 8; a = 4; -4.
a = -4 не подходит по условию задачи.
Итого: 
или х + у – 4 = 0.
Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Уравнение прямой имеет вид: 
, где х1 = у1 = 0; x2 = -2; y2 = -3.
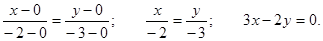
Угол между прямыми на плоскости.
Определение. Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как
.
Две прямые параллельны, если k1 = k2. Две прямые перпендикулярны, если k1 = -1/k2.
Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = lА, В1 = lВ. Если еще и С1 = lС, то прямые совпадают.
Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.
|
|
|
Уравнение прямой, проходящей через данную точку
Перпендикулярно данной прямой.
Определение. Прямая, проходящая через точку М1(х1, у1) и перпендикулярная к прямой у = kx + b представляется уравнением:
Расстояние от точки до прямой.
Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как
.
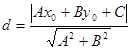Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,
то, решая, получим:
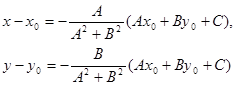
Подставляя эти выражения в уравнение (1), находим:
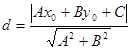. Теорема доказана.
Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.
k1 = -3; k2 = 2 tgj =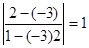 
; j = p/4.
Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.
Находим: k1 = 3/5, k2 = -5/3, k1k2 = -1, следовательно, прямые перпендикулярны.
Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.
Находим уравнение стороны АВ: 
; 4x = 6y – 6;
2x – 3y + 3 = 0; 
Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.
k = 
. Тогда y =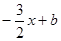 
. Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 
откуда b = 17. Итого: 
.
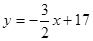Ответ: 3x + 2y – 34 = 0.
Кривые второго порядка.
Кривая второго порядка может быть задана уравнением
Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0.
Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.
1) 
- уравнение эллипса.
2) 
- уравнение “мнимого” эллипса.
3) 
- уравнение точки (0;0)
4) 
- уравнение гиперболы.
5) a2x2 – c2y2 = 0 – уравнение двух пересекающихся прямых.
|
|
|
6) y2 = 2px – уравнение параболы.
7) y2 – a2 = 0 – уравнение двух параллельных прямых.
8) y2 + a2 = 0 – уравнение двух “мнимых” параллельных прямых.
9) y2 = 0 – пара совпадающих прямых.
10) (x – a)2 + (y – b)2 = R2 – уравнение окружности.
|
|
|
